Exercícios de Colisões Inelásticas - Lista de Exercícios Resolvida
Questão 1
Duas partículas e de massas iguais colidem unidimensionalmente ao longo do eixo . Os gráficos a seguir representam as velocidades em função do tempo para cada partícula. Se é o momento linear do sistema formado pelas duas partículas e sua energia cinética, podemos afirmar que nessa colisão
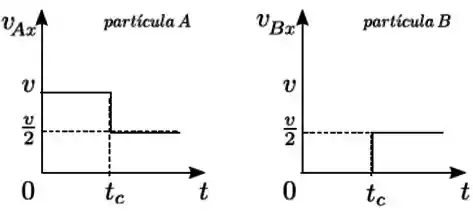
se conserva e não se conserva
se conserva e se conserva
não se conserva e não se conserva
não se conserva e se conserva
e
Ver solução completaQuestão 2
Uma bala de disparada por um rifle penetra e fica retida em um bloco de ligado a uma mola e apoiado sobre uma superfície horizontal sem atrito. O impacto produz uma compressão de na mola. A calibração mostra que uma força de comprime a mola . Calcule o módulo da velocidade do bloco imediatamente após o impacto. Qual era a velocidade inicial da bala?
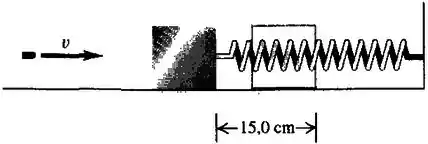
Questão 3
Considere um sistema isolado formado por duas partículas. Suas massas valem e e, num referencial inercial, suas velocidades são, respectivamente,
Estas partículas sofrem uma colisão totalmente inelástica. Qual o valor da energia cinética do sistema, após a colisão?
Ver solução completa
Questão 4
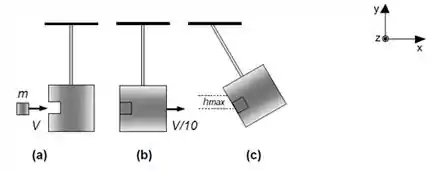
Um pêndulo balístico é um dispositivo utilizado para medir a velocidade de um projétil quando ele deixa o cano de uma arma. Esta velocidade é chamada de velocidade de saída do projétil. Um projétil de massa é disparado horizontalmente contra um bloco de madeira de massa que forma o peso de um pêndulo. O projétil penetra no bloco e o observador mede então a altura máxima atingida pelo conjunto formado pelo bloco e pelo projétil. Responda:
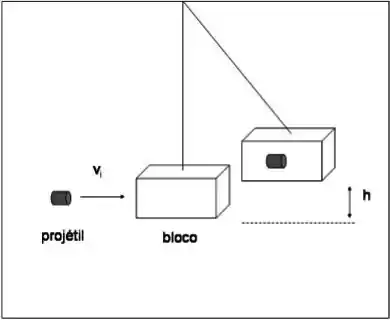
Alguma grandeza é conservada nesta colisão? Por quê?
Qual é a velocidade do sistema projétil + bloco imediatamente após a colisão sabendo que o sistema atinge a altura máxima de ?
Qual é a velocidade inicial do projétil?
Ver solução completaQuestão 5
As esferas (massa ), (massa ) e (massa ) se aproximam da origem deslizando sobre uma mesa de ar sem atrito. As velocidades de e são indicadas na figura. Todas as três esferas atingem a origem ao mesmo instante e ficam coladas. Quais devem ser os componentes e da velocidade inicial de para que os três objetos unidos se desloquem a no sentido do eixo após a colisão? Se possui velocidade encontrada no item (a), qual é a variação da energia cinética do sistema das três esferas ocasionada pela colisão?
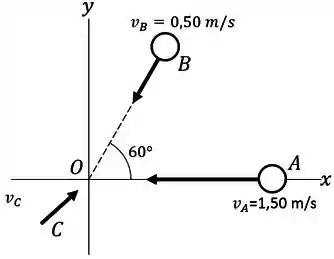
Questão 6
Sobre uma mesa de ar horizontal sem atrito, o disco de hóquei (com massa igual a ) se desloca de encontro ao disco de hóquei (com massa igual a ), que inicialmente está em repouso. Depois da colisão o disco de hóquei possui velocidade igual a da direita para a esquerda e o disco de hóquei possui velocidade igual a da esquerda para a direita. Qual era a velocidade do disco de hóquei antes da colisão? Calcule a variação da energia cinética total do sistema ocorrida durante a colisão.
Ver solução completaQuestão 7
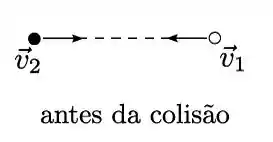
Dois objetos de mesma massa e dimensões desprezíveis colidem no espaço sideral, na ausência de forças externas. A figura mostra um sistema de eixos de um referencial inercial, com seus unitários e . Antes da colisão os objetos se movem ao longo do eixo com velocidades de sentidos opostos, como indicados na figura, e módulos e , nos quais é uma constante dada. Após a colisão, um os objetos adquire velocidade (na figura de baixo apenas um dos objetos é mostrado).
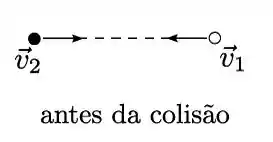
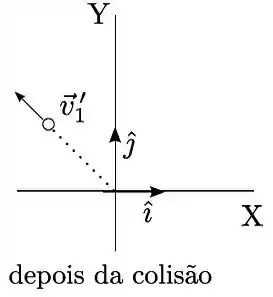
Determine a velocidade do outro objeto após a colisão, expressando sua resposta em termos da constante e dos unitários e .
Determine a razão entre a energia cinética do par de objetos depois da colisão e sua energia cinética antes da colisão; esta colisão é elástica ou inelástica?
Ver solução completaQuestão 8
A figura mostra o resultado de uma colisão entre dois corpos de massas desiguais. Determine:
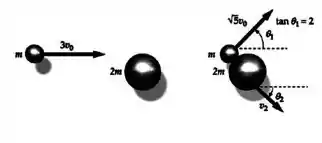
O ângulo
A rapidez da maior massa após a colisão.
Classifique a colisão quanto à variação de energia cinética, justificando sua resposta.
Ver solução completaQuestão 9
Um disco de hóquei está em repouso sobre uma superfície lisa de gelo quando é atingido por outro disco de hóquei que estava inicialmente se movendo a e que passa a se mover sofrendo um desvio de da sua direção original. O disco de hóquei passa a se mover com velocidade formando um ângulo de com a direção original de . As massas dos discos são iguais. Calcule o módulo da velocidadede cada disco de hóquei depois da colisão. Qual a fração da energia cinética inicial do disco de hóquei A que foi dissipada durante a colisão?
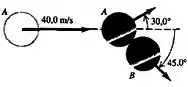
Questão 10
Dois objetos de mesma massa e dimensões desprezíveis colidem no espaço sideral, na ausência de forças externas. A figura mostra um sistema de eixos de um referencial inercial, com seus unitários e . Antes da colisão os objetos se movem ao longo do eixo com velocidades de sentidos opostos, como indicados na figura, e módulos e , nos quais é uma constante dada. Após a colisão, um os objetos adquire velocidade (na figura de baixo apenas um dos objetos é mostrado).
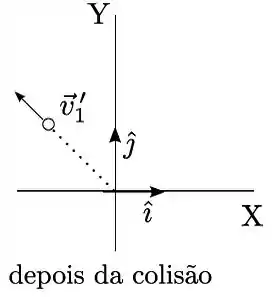
- Determine a velocidade do outro objeto após a colisão, expressando sua resposta em termos da constante e dos unitários e .
- Determine a razão entre a energia cinética do par de objetos depois da colisão e sua energia cinética antes da colisão; esta colisão é elástica ou inelástica?
Questão 11
Duas partículas de mesma massa caem verticalmente e colidem com uma mesa horizontal lisa com a mesma velocidade. Uma das partículas colide elasticamente com a mesa sem sair da vertical e a outra colide de forma totalmente inelástica com a mesa. Denotando por a variação do momento linear da primeira particular na colisão elástica, por a variação do momento linear da segunda partícula em sua colisão totalmente inelástica, podemos afirmar que
- e
Questão 12
A figura mostra uma rampa com um trecho horizontal e o ponto a uma altura do trecho horizontal. Um bloco de massa é abandonado em repouso sobre a rampa no ponto e um bloco idêntico está em repouso sobre a rampa entre e .
A parte do trecho horizontal tem comprimento , e coeficiente de atrito cinético com os blocos, já o restante da rampa é totalmente liso.Ao final do trecho horizontal , entre os pontos e , encontra-se uma mola de constante elástica fixada à rampa em .O bloco abandonado em sofre uma colisão perfeitamente inelástica com o outro bloco e o conjunto se move na horizontal até atingir a mola e comprimi-la até parar.
Considere como dados e o módulo da aceleração da gravidade.
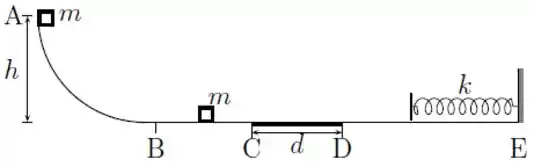
Considerando as dimensões dos blocos desprezíveis, calcule
a) a velocidade do bloco abandonado em imediatamente antes de colidir com o outro bloco;
b) a velocidade do conjunto imediatamente depois da colisão;
c) a velocidade do conjunto imediatamente antes de colidir com a mola;
d) o máximo comprimento de compressão da mola.
Ver solução completaQuestão 13
Duas partículas com velocidades iniciais perpendiculares (figura) colidem de forma totalmente inelástica. Seja o momento linear total do sistema composto pelas duas partículas (, seu módulo) e a energia cinética total deste sistema. Comparando os valores de e antes e depois da colisão, pode-se afirmar que
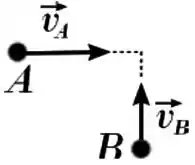
(a) é conservado, é reduzido, porém não a zero.
(b) é conservado, é conservado;
(c) é reduzido a zero, é reduzido a zero;
(d) é conservado, é reduzido a zero;
(e) é reduzido, porém não a zero, é reduzido, porém não a zero;
Ver solução completaQuestão 14
Se todas as três colisões na figura abaixo são perfeitamente inelásticas, qual ou quais geram a maior força de deformação nos carros?
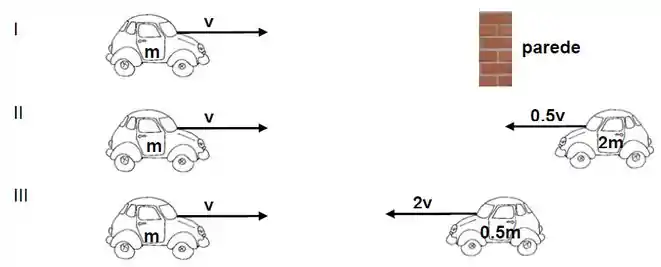
a) I.
b) II.
c) III.
d) I e II.
e) I e III.
f) II e III.
g ) todas as três.
Ver solução completaQuestão 15
Um objeto A de massa está se movendo ao longo do eixo , quando ele colide inelasticamente com um objeto, B, de massa , vindo a parar completamente. Se o objeto A tem uma velocidade inicial , qual é a energia cinética do objeto B?
a)
b)
c)
d)
e)
Ver solução completaQuestão 16
Dois pêndulos de igual comprimento estão situados inicialmente como na figura. O pêndulo da esquerda é solto da altura e colide contra o outro, que estava inicialmente em repouso. Nesta colisão vamos desprezar a massa dos fios e quaisquer efeitos de atrito.
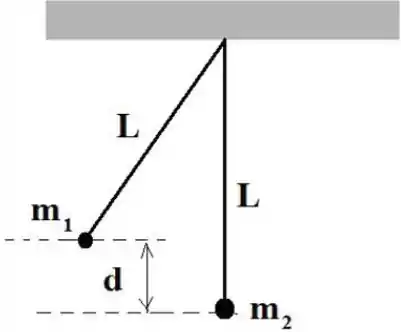
Suponha primeiramente que a colisão é elástica.
a) Escreva as equações das leis de conservação que caracterizam a colisão em si, relacionando as quantidades relevantes logo antes e logo depois da colisão.
b) Seja o caso particular em que . Encontre a altura que se eleva o corpo . (Faça os cálculos, não use respostas prontas!)
Agora suponha que a colisão é totalmente inelástica.
c) Se , a que altura se eleva o centro de massa do conjunto após a colisão?
Ver solução completaQuestão 18
1 – Uma bala de é disparada horizontalmente com velocidade de contra um bloco de madeira de , inicialmente em repouso sobre uma superfície horizontal. A bala atravessa o bloco e emerge com uma velocidade reduzida para . O bloco desliza ao longo da superfície até uma distância de da sua posição inicial e depois para.
a) Qual é o coeficiente de atrito cinético entre o bloco e a superfície?
b) Qual a diminuição da energia cinética da bala?
c) qual é a energia cinética do bloco no instante em que a bala emerge do bloco?
Ver solução completaQuestão 19
6) Uma haste delgada e homogênea de comprimento L e massa M que se encontra inicialmente em repouso em uma mesa é atingida ortogonalmente a uma distância d de seu centro por um pequeno disco de massa M/3 que fica a ela aderido após a colisão. Não existindo atrito com a mesa, podemos afirmar que nesse processo de colisão no sistema formado pela haste e o disco não será conservado(a):
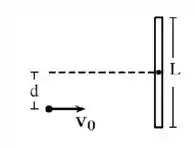
- Momento linear do sistema.
- Momento angular do sistema em relação ao centro de massa do sistema.
- Momento angular do sistema em relação ao centro de da barra.
- Todas as quantidades mencionadas se conservam.
- Energia mecânica do sistema.
Questão 20
Durante a madrugada, um carro de luxo, de massa total igual a 2400 Kg, bate na traseira de um carro de massa total 1200 kg, que estava parado num sinal vermelho. O motorista do carro de luxo alega que o outro estava com as luzes apagadas, e que ele vinha reduzindo a marcha ao aproximar-se do sinal, estando a menos de 10 km/h quando o acidente ocorreu. A perícia constata que o carro de luxo arrastou o outro de uma distância igual a 10,5 m, e estima o coeficiente de atrito cinético com a estrada no local do acidente em 0,6. Calcule a que velocidade o carro de luxo vinha realmente.
Ver solução completaQuestão 21
4 – Responda cada um dos itens:
a) Numa colisão totalmente inelástica entre dois corpos de massa e , onde está em repouso, qual deve ser a relação entre as massas e para que a velocidade final seja da velocidade inicial?
b) Considere uma colisão entre dois corpos ( e ) de massas iguais. O corpo está inicialmente em repouso. Após a colisão, a velocidade de cada um deles será necessariamente menor que a velocidade inicial do corpo . Ou seja, as constantes definidas como e são necessariamente menores que . Nestas definições os índices e (inicial e final) se referem às situações antes e depois da colisão respectivamente. Qual deve ser a relação entre as constantes e para que a colisão seja totalmente elástica?
Ver solução completaQuestão 24
Um objeto A de massa e velocidade de módulo colide com outro objeto B de massa , inicialmente em repouso. As velocidades dos objetos antes e depois da colisão têm a mesma direção e a colisão ocorre em um intervalo de tempo ∆t. Se o módulo da força média nesse intervalo exercida pelo objeto A sobre o B é f, o valor de ∆t para que a colisão seja perfeitamente inelástica é:
Questão 25
(FUVEST-SP) Dois corpos se movem com movimento retilíneo uniforme num plano horizontal onde as forças de atrito são desprezíveis. Suponha que os dois corpos, cada com energia cinética de 5 J, colidam frontalmente, fiquem grudados e parem imediatamente, devido à colisão.
(a) Qual foi a quantidade de energia mecânica que não se conservou na colisão ?
(b) Qual era a quantidade de movimento linear do sistema, formado pelos dois corpos, antes da colisão ?
Ver solução completaQuestão 26
Um bloco de massa desliza sem velocidade inicial ao longo de uma rampa sem atrito a partir de uma altura e colide com um bloco de massa , inicialmente em repouso. Após a colisão, o bloco desliza em uma região com coeficiente de atrito cinético até finalmente parar após percorrer uma distância . Qual é o valor de se a colisão for:
elástica?
perfeitamente inelástica?
Dica: Este exercício fica mais fácil de resolver se você deixar para substituir os valores das várias grandezas apenas perto do final, e só então fazer as contas.

Questão 27
Dois pequenos discos (que podem ser considerados como partículas), de massa e , se deslocam sobre uma mesa horizontal, sem atrito, conforme mostra a figura abaixo. Inicialmente eles possuem velocidades em direções perpendiculares de mesmo módulo . Num certo instante, ocorre uma colisão e o sistema passa a se deslocar em conjunto a partir desse momento. As respostas dos itens abaixo devem ser dadas em função de e .
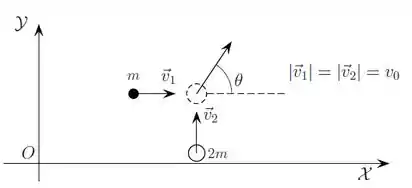
a) Calcule o módulo de , que é a velocidade depois que os discos se movimentam juntos e o ângulo que esse vetor faz com o eixo . Indique qual(quais) Lei(s) de conservação está(ão) sendo utilizada(s) e o porquê.
b) Calcule a variação da energia cinética entre os instantes anterior e posterior à colisão.
c) Calcule o vetor velocidade do centro de massa do sistema antes de ocorrer a colisão.
Ver solução completaQuestão 28
Um carrinho de massa se move sobre uma superfície sem atrito com uma velocidade = 2m/s para a direita, quando uma explosão ocorre e o carrinho se divide em duas partes: A e B. Uma parte do carrinho com massa continua a se mover para a direita com
uma velocidade . Qual a velocidade da outra parte do carrinho de massa ?
a) 4m/s para a esquerda
b) 2m/s para a esquerda
c) 1m/s para a esquerda
d) 0
e) 1m/s para a direita
Ver solução completaQuestão 29
Um bloco de massa colide com velocidade com um pêndulo de massa desconhecida em repouso. . Imediatamente após a colisão ambos adquirem a mesma velocidade . . Após a colisão, como ilustrado na figura , a componente vertical da posição do centro de massa do conjunto tem uma variação máxima igual a . Despreze atritos.
- Usando o sistema de coordenadas indicado, determine o impulso provocado pelo pêndulo no bloco, durante a colisão.
- Utilizando princípios de conservação de energia determine , a altura máxima alcançada.
- Determine a massa do pêndulo.
Questão 30
Dois corpos e , ambos de massa , sofrem uma colisão. As velocidades antes da colisão são e . Após a colisão, a velocidade de é . A variação da energia cinética na colisão foi:
(A)
(B)
(C) zero
(D)
(E)
Ver solução completaQuestão 31
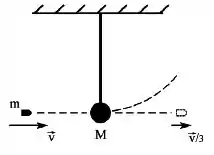
Na figura é representada uma bala de massa e velocidade que atravessa uma esfera de massa pendurada por uma haste de comprimento e de massa desprezível. A bala emerge da esfera com velocidade . Qual é a fração que a energia cinética final representa da energia cinética inicial?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 32
Um bloco de massa desliza em uma superfície sem atrito e explode em dois fragmentos de massas e . A velocidade do bloco antes da explosão era e o momento linear do fragmento 1 após a explosão é . O módulo da velocidade do fragmento 2 após a explosão é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 33
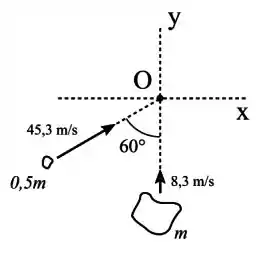
Dois asteroides, um de massa e outro de massa , estão se movendo no espaço, como mostra a figura. Os asteroides colidem no ponto e a colisão é perfeitamente inelástica. Qual é o ângulo que a velocidade do objeto único resultante da colisão faz com o eixo ?
(a)
(b)
(c)
(d)
(e)
Questão 34
Uma partícula (1) de massa se move na direção positiva do eixo com velocidade no topo de uma mesa sem atrito de altura . Ao final da mesa encontra-se uma partícula (2) de massa . Ignore a dimensão das partículas.
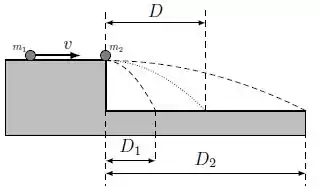
b) Supondo que a colisão entre as partículas foi perfeitamente inelástica, encontre a nova distância percorrida pelas partículas grudadas, em relação a base da mesa (na figura a distância é representada por , a trajetória é descrita pela linha pontilhada). O tempo de queda também é .
Ver solução completaQuestão 35
Uma bola de massa desloca-se com velocidade num plano horizontal sem atrito. Choca-se frontalmente com uma outra bola idêntica em repouso e prossegue seu movimento na mesma direção e no mesmo sentido com velocidade .
Calcule a velocidade final da segunda bola. Verifique se há conservação de energia cinética.
Ver solução completaQuestão 36
Duas massas de modelar deslizam sobre uma superfície horizontal de gelo, sem atrito. As massas possuem velocidades iniciais , e colidem de forma que seguem juntas com velocidade , conforme a Figura abaixo.
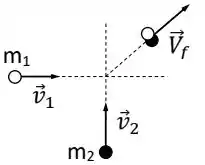
Considere as afirmativas abaixo:
I) A energia mecânica total das massas depois da colisão é a mesma que antes da colisão.
II) O momento linear total das massas depois da colisão é o mesmo que antes da colisão.
III) O momento linear da massa m1 depois da colisão é o mesmo que antes da colisão.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
a) I
b) II
c) III
d) I e II
e) I e III
f) II e III
g) Todas
h) Nenhuma
Ver solução completaQuestão 37
Um bloco de massa encontra-se inicialmente mantido em repouso, comprimindo de uma mola de constante elástica (ver Figura 3). Quando o bloco liberado, ele perde contato com a mola antes do ponto . Não existe atrito antes do ponto .
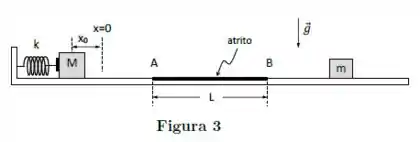
(a) Calcule a velocidade do bloco no ponto .
(b) Entre os pontos e o bloco atravessa uma região de comprimento com Coeficiente de atrito cinético . Calcule o trabalho realizado pela força de atrito nessa região. Considere .
(c) Calcule a velocidade do bloco no ponto
(d) Após o ponto , o atrito deixa de existir e o bloco realiza uma colisão perfeitamente inelástica com um outro bloco de massa que se encontrava inicialmente parado. Calcule a velocidade dos blocos após a colisão.
Ver solução completaQuestão 38
Em um sistema de partículas em que não há forças externas é correto afirmar que:
Sempre há conservação de energia mecânica do sistema
Sempre há conservação do momento linear total do sistema
Sempre há conservação da Energia Cinética total do sistema
Forças dissipativas internas podem reduzir o momento linear total
Pode haver transferência do momento linear para energia cinética, através da ação de forças conservativas.
Ver solução completaQuestão 39
Um caminhoneiro distraído dirige seu caminhão de em uma rua e não vê um carro de massa à sua frente que está parado no semáforo. Ele acaba colidindo com a traseira do carro. O caminhão e o carro ficam enroscados um no outro e deslizam juntos em linha reta por uma distância de antes de ambos pararem. Sabendo que o coeficiente de atrito cinético entre a superfície da rua e os dois veículos é , encontre:
a velocidade do conjunto (caminhão + carro) imediatamente após a colisão.
a velocidade do caminhão antes da colisão.
Ver solução completaQuestão 40
Um astronauta está flutuando no espaço, segurando uma caixa de massa . A massa do astronauta juntamente com todo seu equipamento (excetuando a caixa) é de . Ele lança a caixa a uma velocidade de para a direita. Após o lançamento, sua velocidade será de:
para a esquerda
para a esquerda
para a esquerda
m/s para a esquerda
m/s para a esquerda
Ver solução completaQuestão 41
Uma bala é atirada a uma velocidade de em um bloco de madeira, atravessando-o e saindo a uma velocidade de sem desviar sua trajetória. Se a massa da bala é de e a do bloco é de , qual a velocidade final do bloco?
Ver solução completa
Questão 42
Em um cruzamento da cidade de São Paulo, um carro compacto com massa de que se deslocava de oeste para leste colide com uma picape com massa de que se deslocava do sul para o norte e avançou o sinal vermelho (figura abaixo). Em virtude da colisão, os dois veículos ficam engavetados e após a colisão se deslocam a na direção nordeste. Calcule o módulo da velocidade de cada veículo antes da colisão. Estava chovendo muito durante a colisão, e o atrito entre os veículos e a estrada pode ser desprezado.
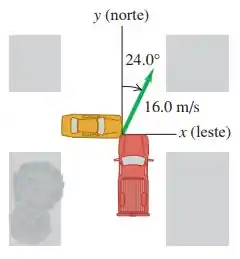
Questão 43
O bloco A de massa m parte do repouso e desce uma rampa de altura h sem atrito até um trecho horizontal quando sofre uma colisão com o bloco B, com massa 2m, inicialmente parado e ainda na parte sem atrito do trecho. Após a colisão, os blocos A e B permanecem grudados entre si e percorrem uma distância d, sobre uma superfície com coeficiente de atrito cinético , até pararem. Determine (em função das grandezas fornecidas: que julgar necessárias):
- A velocidade do bloco A imediatamente antes da colisão;
Questão 44
A posição em função do tempo de dois corpos que colidem está representada no gráfico abaixo. A posição do centro de massa desse sistema também está representada.
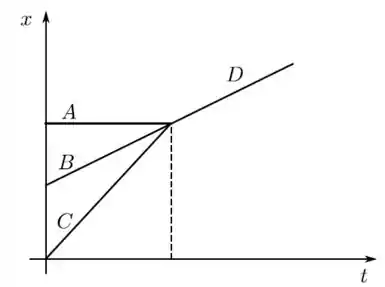
A partir da análise do gráfico são feitas as seguintes afirmações:
I. A colisão é inelástica.
II. O segmento B representa a posição de um dos corpos antes da colisão.
III. A resultante das forças externas é nula.
IV. Os dois corpos estavam em movimento apenas antes da colisão.
Marque a opção que indica aquelas que são CORRETAS:
(a) Somente I e III
(b) Somente II e IV
(c) Somente I, II e III
(d) Somente II, III e IV
(e) Todas
(f) Nenhuma
Ver solução completaQuestão 45
Um motorista está dirigindo um carro fazendo uma curva em uma rua de mão única a 30 km/h. Quando ele sai da curva nota vindo em sua direção um carro idêntico ao seu com a mesma velocidade. Como tudo acontece muito rápido, ele só tem duas escolhas: colidir com o carro vindo em sua direção ou desviar para colidir, também de frente, com um muro de concreto. Supondo as duas colisões totalmente inelásticas e de igual duração, qual seria a melhor decisão para provocar a menor deformação sobre seu carro?
a) colidir com o outro carro.
b) colidir com o muro.
c) tanto faz.
d) preciso de mais informações.
Ver solução completaQuestão 46
Um bloco de madeira e um revólver estão fixos nas extremidades opostas de uma longa plataforma montada sobre um trilho de ar (atrito desprezível). O bloco e o revólver estão separados por uma distância . Todo o sistema está inicialmente em repouso. O revólver dispara uma bala que o abandona com uma velocidade , atingindo o bloco e nele se encravando. A inércia da bala é e a inércia do sistema revólver–plataforma–bloco é .

Qual é a velocidade da plataforma logo após a bala é disparada?
Qual é a velocidade da plataforma imediatamente após a bala atingir o repouso dentro do bloco?
Qual é a distância percorrida pela plataforma enquanto a bala está em trânsito entre o revólver e o bloco?
Ver solução completaQuestão 47
Um caminhão de massa é incapaz de controlar os freios e colide com um carro de massa em repouso. Como resultado da colisão, o caminhão para instantaneamente. O carro desliza em frente, parando após metros. O coeficiente de atrito entre os pneus do carro e a estrada é de . Se necessário, considere . Com que magnitude de velocidade o caminhão estava se movendo no momento da colisão?
Ver solução completaQuestão 48
Uma pessoa de 60 kg, correndo inicialmente com uma velocidade de 4 m/s pula em um carrinho de 120 kg que encontra-se inicialmente em repouso. Ao pular, a pessoa escorrega, vindo a deslizar sobre a superfície superior do carrinho até parar, ficando em repouso em relação a este. O coeficiente de atrito cinético entre a pessoa e a superfície do carrinho é de 0,4. O atrito entre o carrinho e o solo pode ser desprezado. Pede-se calcular:
- A velocidade final do sistema carrinho mais pessoa em relação ao solo.
- A força de atrito atuando sobre a pessoa enquanto ela está deslizando.
- O trabalho realizado pela força de atrito e o deslocamento da pessoa sobre a superfície do carrinho em relação ao carrinho.
- A variação da energia cinética do carrinho.
Questão 49
Uma bola de borracha de massa desliza sobre uma superfície horizontal sem atrito e colide com um anteparo fixo. O módulo da velocidade da bola é . A colisão faz um ângulo com a face do anteparo como ilustra a figura. A bola é refletida a mesma velocidade escalar e com o mesmo ângulo. O contato entre a bola e o anteparo dura . Utilize o sistema de coordenadas indicado.
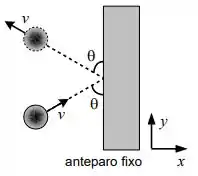
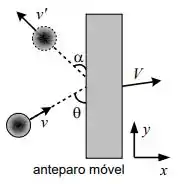
c) Suponha agora uma nova colisão, com a bola tendo a mesma velocidade inicial de módulo e ângulo com a face do anteparo. Mas agora o anteparo pode se mover livremente e sua massa é dada por . Sabendo que o módulo da velocidade da bola refletida é imediatamente depois da colisão e que ela faz um ângulo com o anteparo, calcule a velocidade do anteparo. Determine se a colisão foi elástica ou inelástica.
Questão 50
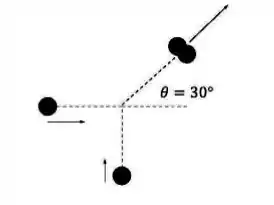
Duas partículas de mesma massa e traçando trajetórias ortogonais colidem, e seguem grudadas após a colisão. O ângulo que as partículas grudadas fazem com a direção original da primeira partícula é de , conforme desenho abaixo. Qual a razão entre as velocidades iniciais das partículas?
Ver solução completa
Questão 51
12 - Lulas e polvos se impulsionam expelindo água. Eles fazem isso armazenando água em uma cavidade e repentinamente contraindo essa cavidade para expelir a água através de um orifício. Uma lula de (incluindo a água) está em repouso quando de repente avista um perigoso predador. Se a lula possui de água em sua cavidade, com qual módulo da velocidade ela deve expelir essa água para subitamente atingir uma velocidade com módulo de e assim conseguir escapar do predador? Despreze qualquer efeito da força de arraste da água circundante.
A)
B)
C)
D)
E)
Ver solução completaQuestão 52
Duas partículas com velocidades iniciais perpendiculares (figura) colidem de forma totalmente inelástica. Seja p o momento linear total do sistema composto pelas duas partículas (|p|, seu módulo) e K a energia cinética total deste sistema. Comparando os valores de p e K antes e depois da colisão, pode-se afirmar que:
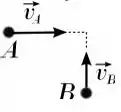
a) p é conservado, K é reduzido, porém não a zero;
b) p é conservado, K é conservado;
c) |p| é reduzido a zero, K é reduzido a zero;
d) p é conservado, K é reduzido a zero;
e) |p| é reduzido, porém não a zero, K é reduzido, porém não a zero;
f) |p| é aumentado, K é conservado;
Ver solução completaQuestão 53
Considere a colisão mostrada na figura. As massas dos blocos bem como as velocidades antes e depois da colisão são fornecidas. Assinale a alternativa correta:

a) A colisão não é possível porque o momento linear não é conservado
b) A colisão é parcialmente não elástica
c) A colisão é perfeitamente elástica
d) Há um aumento de energia cinética
e) A colisão é totalmente não elástica
Ver solução completaQuestão 54
7. Um projétil de é disparado horizontalmente com uma rapidez de contra um bloco de madeira de . O bloco de madeira se encontra em repouso. Após a colisão, o projétil fica incrustado no bloco de madeira. Sabendo que o coeficiente de atrito cinético entre o bloco e o solo é de , determine a distância aproximada percorrida pelo bloco após a colisão.
Questão 55
10. Duas bolas de mesmo massa sofrem uma colisão. A colisão é unidimensional. A bola tem rapidez inicial e colide com a bola em repouso. O gráfico da posição em função do tempo da bola é mostrado abaixo. A seta azul marca o instante da colisão ().
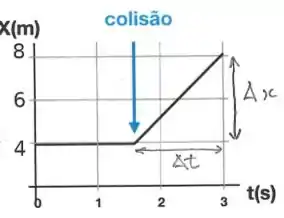
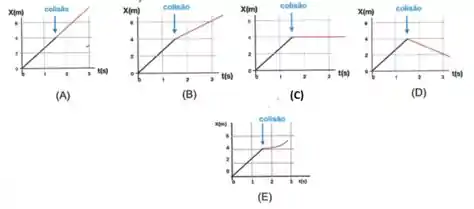
Qual das opções representa corretamente a posição em função do tempo para a bola ?
Questão 56
Um projétil de massa colide com velocidade contra um bloco de madeira de massa . O projétil se aloja dentro do bloco após a colisão. O sistema {bloco+ projétil} desliza sobre uma superfície horizontal cujo coeficiente de atrito cinético é .

Qual é o módulo do deslocamento até que o sistema {bloco+projétil} fique em repouso ?
A)
B)
C)
D)
E)
Ver solução completaQuestão 57
7. Um projétil de é disparado horizontalmente com uma rapidez de contra um bloco de madeira de . O bloco de madeira se encontra em repouso. Após a colisão, o projétil fica incrustado no bloco de madeira. Sabendo que o coeficiente de atrito cinético entre o bloco e o solo é de , determine a distância aproximada percorrida pelo bloco após a colisão.
Questão 58
Um objeto A de massa está se movendo ao longo do eixo , quando ele colide inelasticamente com um objeto de massa , vindo a parar completamente. Se o objeto A tem uma velocidade inicial , qual é a energia cinética do objeto B?
(A) ;
(B);
(C) ;
(D) ;
(E) ;
Ver solução completaQuestão 59
Na Fig. 9-59, uma bala de que se move verticalmente para cima a se choca com um bloco de inicialmente em repouso, passa pelo centro de massa do bloco e sai do outro lado com uma velocidade de . Qual é a altura máxima atingida pelo bloco em relação à posição inicial?
Questão 60
(Cap 9 – Ex 59) Na Fig. 9-65, o bloco 1 (com uma massa de ) está se movendo para a direita com uma velocidade escalar de e o bloco 2 (com uma massa de ) está se movendo para a direita com uma velocidade escalar de . A superfície não tem atrito e uma mola com uma constante elástica de está presa no bloco 2. Quando os blocos colidem, a compressão da mola é máxima no instante em que os blocos têm a mesma velocidade. Determine a máxima compressão da mola .
Ver solução completaQuestão 62
Um carro parte do repouso com aceleração constante de módulo e após percorrer uma certa distância, ele colide com um caminhão. Imediatamente antes de colidirem, o carro e caminhão tinham velocidades de mesmo módulo em direções perpendiculares e, após a colisão eles passam a se movimentar juntos. Sabendo que caminhão tem uma massa cinco vezes maior do que a do carro, responda as perguntas abaixo.
a) Qual a distância percorrida pelo carro desde o instante em que parte do repouso até aquele em que colide com o caminhão?
b) Qual o módulo da velocidade do sistema carro-caminhão imediatamente após a colisão?
c) Qual é o trabalho realizado pelas forças internas do sistema carro-caminhão durante a colisão?
Ver solução completaQuestão 64
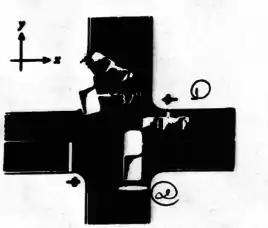
Um carro de viajando para oeste colide com numa interseção com uma caminhonete de viajando para o Norte com módulo de velocidade conforme mostra a figura.Após a colisão, os dois veículos vão juntos para o canteiro da pista, saindo com um ângulo de à esquerda da caminhonete.
Dados:
- Calcule o modulo da velocidade do carro antes da colisão.
- Qual é a velocidade ( em termos dos vetores unitários e do centro de massa imediatamente após a colisão?
- Calcule a razão entre as energias cinéticas antes e depois da colisão. A colisão é elástica?
Questão 65
Um rojão, lançado segundo um ângulo de , explode em dois fragmentos ao atingir sua altura máxima, de m; os fragmentos são lançados horizontalmente. Um deles, de massa igual a , cai no mesmo plano vertical da trajetória inicial, a de distância do ponto de lançamento. O outro fragmento tem massa igual a .
(c) Qual é a energia mecânica liberada pela explosão?
Ver solução completaQuestão 66
Um rojão, lançado segundo um ângulo de , explode em dois fragmentos ao atingir sua altura máxima, de m; os fragmentos são lançados horizontalmente. Um deles, de massa igual a , cai no mesmo plano vertical da trajetória inicial, a de distância do ponto de lançamento. O outro fragmento tem massa igual a .
(b) Quais são as velocidades comunicadas aos dois fragmentos em consequência da explosão?
Ver solução completaQuestão 67
Três partículas de massa estão presas a hastes de tamanho e massas desprezíveis, como uma hélice. O sistema pode girar em torno de um eixo fixo que passa pelo seu centro, , e inicialmente possui velocidade angular . Um chiclete de massa incide com velocidade conforme a figura, e realiza uma colisão perfeitamente inelástica com uma das massas .
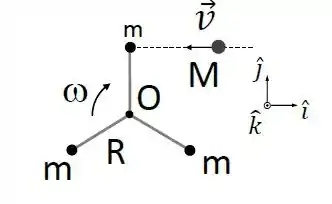
Considere que . Para que o sistema pare completamente após a colisão é necessário que tenha módulo
(A)
(B)
(C)
(D)
(E)
(F)
(G)
(H)
Ver solução completaQuestão 68
Dois pêndulos de comprimento estão suspensos juntos conforme a figura abaixo. O pêndulo (de massa ) é solto a partir do repouso de uma altura enquanto que o pêndulo (de massa ) está em repouso na posição vertical.
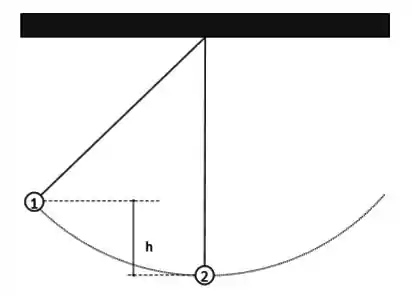
Considerando inicialmente que a colisão é elástica determine:
A velocidade do pêndulo imediatamente antes do choque.
A velocidade de cada pêndulo imediatamente depois do choque.
Supondo agora que a colisão seja inelástica e os dois pêndulos fiquem grudados após a colisão, qual a máxima altura que os dois pêndulos atingem?
Quanta energia foi dissipada na colisão inelástica?
Dado: .
Ver solução completaQuestão 69
A figura mostra dois veículos que colidem de modo totalmente inelástico num cruzamento . A velocidade dos escombros conjuntos tem valor imediatamente após a colisão e direção que faz com o eixo . O veículo , que vinha no eixo da figura, tem massa , e o veículo tem massa . Considere o sistema isolado durante a colisão.
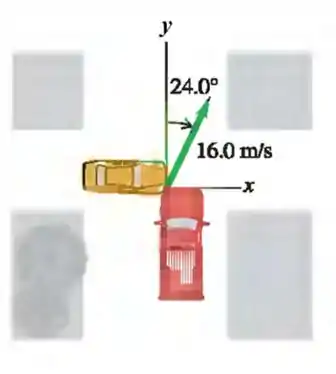
Forneça o vetor momento do centro de massa do sistema imediatamente depois da colisão, , e imediatamente antes da colisão, . Justifique.
Qual a velocidade escalar de cada veículo antes da colisão?
Forneça o vetor força que atuou sobre o veículo , , sabendo que a colisão teve duraçãoo de .
Ver solução completaQuestão 70
Um pêndulo balístico é um dispositivo utilizado para medir a velocidade de um projétil quando ele deixa o cano de uma arma. Esta velocidade é chamada de velocidade de saída do projétil. Um projétil de massa é disparado horizontalmente contra um bloco de madeira de massa que forma o peso de um pêndulo. O projétil penetra no bloco e o observador mede então a altura máxima atingida pelo conjunto formado pelo bloco e pelo projétil. Responda:
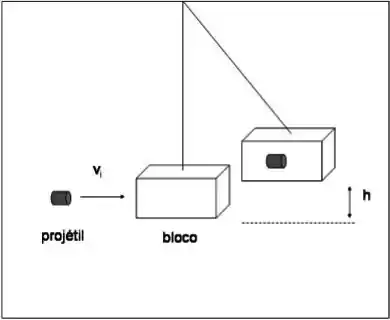
a) alguma grandeza é conservada nesta colisão? Por que?
b) qual é a velocidade do sistema projétil + bloco imediatamente após a colisão sabendo que o sistema atinge a altura máxima de ?
c) qual é a velocidade inicial do projétil?
Ver solução completaQuestão 71
Um corpo se move na direção x positiva com rapidez v. Um segundo corpo, cuja massa é igual à metade da massa do primeiro, move-se no sentido oposto com a mesma rapidez. Os dois se envolvem em uma colisão frontal e completamente inelástica. A rapidez do sistema após a colisão é:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 72
Uma bola de massa com velocidade de colide com outra bola de massa inicialmente em repouso. Supondo a colisão perfeitamente inelástica, qual a velocidade das bolas após a colisão e a energia dissipada no processo?
e
e
e
e
e
Ver solução completaQuestão 73
Uma bola de aço de massa igual a é solta de uma altura de sobre uma barra de aço horizontal. A bola é rebatida até uma altura de .
- Calcule o impulso comunicado para a bola durante a colisão.
Questão 74
Uma bola de aço de massa igual a é solta de uma altura de sobre uma barra de aço horizontal. A bola é rebatida até uma altura de .
- Sabendo que a bola permanece em contato com a barra durante , calcule a força média exercida sobre a bola durante a colisão.
Questão 75
Uma pedra de está em repouso sobre uma superfície horizontal sem atrito. Uma bala de , se deslocando horizontalmente a , colide com a pedra e ricocheteia ao longo da superfície com velocidade de em uma direção ortogonal à sua velocidade inicial.
- Determine o módulo, a direção e o sentido da velocidade da pedra após o impacto.
Questão 76
Uma pedra de está em repouso sobre uma superfície horizontal sem atrito. Uma bala de , se deslocando horizontalmente a , colide com a pedra e ricocheteia ao longo da superfície com velocidade de em uma direção ortogonal à sua velocidade inicial.
- A colisão é perfeitamente elástica?
Questão 77
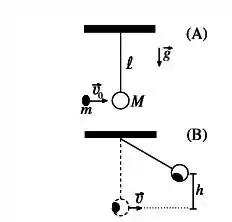
Um corpo de massa encontra-se pendurado na vertical por uma haste de comprimento e massa desprezível. Uma partícula de massa atinge o corpo com velocidade (figura()). Imediatamente após a colisão os dois corpos se deslocam unidos com velocidade . Considere a aceleração gravitacional no local .
(a) Determine .
(b) Após a colisão o sistema se desloca verticalmente de uma altura , quando fica momentaneamente em repouso (figura()). Calcule .
Questão 78
Uma esfera de chumbo de está preso a um gancho suspenso por um fio fino com de comprimento e está livre para oscilar formando um círculo completo. Subitamente a esfera de chumbo é atingida horizontalmente por um dardo de aço de que a penetra. Qual deve ser a velocidade inicial mínima do dardo para que o conjunto dê uma volta completa após a colisão?
Ver solução completaQuestão 79
Dois veículos se encontram em uma via horizontal. O veículo 2 se encontra em repouso quando o veículo 1, de massa = 5, colide com o veículo 2. Após a colisão eles ficam grudados e possuem uma velocidade v = 1,0m/s. Qual é a velocidade do veículo 1 antes da colisão, considerando que a colisão é perfeitamente inelástica?
a) 1,5 m/s
b) 1,2 m/s
c) 1,1 m/s
d) 1,0 m/s
e) 0,80 m/s
Ver solução completaQuestão 80
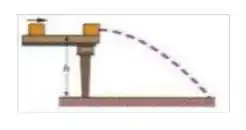
Na figura, uma caixa de sapatos de desliza em uma mesa horizontal sem atrito e colide com outra caixa de sapatos de inicialmente em repouso na extremidade da mesa, a uma altura do chão. A velocidade da caixa de é de imediatamente antes da colisão. Se as caixas grudam uma na outra por haver cola nas faces de contato, qual a energia cinética do conjunto imediatamente de atingir o chão?
Ver solução completa
Questão 81
Um bloco , com massa , está inicialmente em repouso, comprimindo de uma mola de constante elástica . Após ser liberado, o bloco se desprende da mola com velocidade , dirigindo-se a outro bloco idêntico (bloco ) situado mais à frente na mesma superfície horizontal sem atrito. O bloco está inicialmente parado. Depois da colisão frontal entre os dois blocos, eles saem unidos com velocidade . Mais adiante, o conjunto dos dois blocos colide elasticamente com uma esfera de massa , inicialmente em repouso, que está conectada a um fio ideal de comprimento Considere .
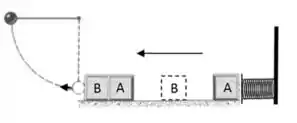
(a) Determine .
(b) Determine a perda relativa de energia cinética na colisão entre e .
Supondo que , determine:
(c) o comprimento do fio para que, como consequência da colisão sofrida pela esfera, o fio descreva um arco de exatamente , conforme a figura.
Ver solução completaQuestão 82
Uma bala de massa e velocidade é disparada contra um bloco de massa , que inicialmente se encontra em repouso na borda de um poste de altura , conforme mostra a figura abaixo. A bala aloja-se no bloco que, devido ao impacto, cai no solo. Sendo a aceleração da gravidade, e não havendo atrito nem resistência de qualquer natureza, calcule o módulo da velocidade com que o conjunto atinge o solo
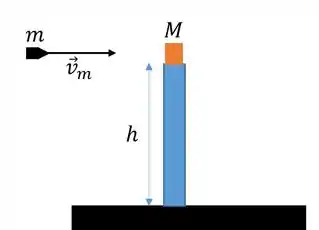
a)
b)
c)
d)
e)
Ver solução completaQuestão 83
Q - Considere uma bala disparada horizontalmente contra dois blocos inicialmente em repouso sobre uma superfície sem atrito. A bala atravessa o bloco e fica alojada no bloco . A velocidade final do bloco é e do bloco é . Desprezando o material removido do bloco pela bala e a resistência do ar e considerando que ; ; ;
calcule a velocidade da bala ao entrar no bloco ;
calcule a velocidade da bala ao entrar no bloco ;
faça o gráfico de da colisão entre a bala e o bloco ;
faça o gráfico de da colisão entre a bala e o bloco .
Ver solução completaQuestão 84
Um bloco sobre um piso horizontal pode estar inicialmente: em repouso, em movimento no sentido positivo do eixo ou em movimento no sentido negativo do mesmo eixo. O bloco explode em dois pedaços que continuam a se mover ao longo do eixo . Suponha que o bloco e os dois pedaços formem um sistema fechado e isolado. A figura mostra seis possibilidades para o gráfico dos momentos do bloco e dos pedaços em função do tempo . Pode-se dizer que:
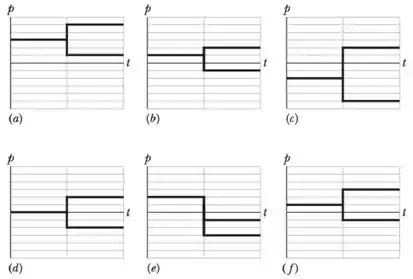
(a) As situações , , , são físicamente impossíveis.
(b) Todas as situações são físicamente impossíveis.
(c) As situações , , , são físicamente impossíveis.
(d) As situações , , , são físicamente impossíveis.
(e) Todas as situações são físicamente possíveis.
Ver solução completaQuestão 85
Duas partículas podem deslocar-se sem atrito sobre um plano horizontal , com vetores unitários e na direção dos eixos e positivos, respectivamente. A partícula , de massa , inicialmente desloca-se com velocidade ao longo do eixo .
Ela então se choca com a partícula , de massa , que estava inicialmente parada na origem do sistema de coordenadas (vide figura). Após o choque, sai com velocidade .
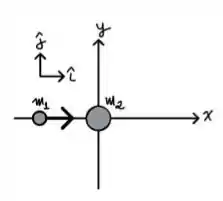
(a) Calcule, em termos dos vetores unitários e , a velocidade de após o choque, explicitando a(s) grandeza(s) conservada(s). Justifique sua resposta.
(b) Calcule a variação da energia cinética que ocorreu devido ao choque.
(c) Calcule, em termos dos vetores unitários e , o vetor-posição do centro de massa do sistema segundos após o choque.
Ver solução completaQuestão 86
Qual das afirmações é verdadeira sobre uma colisão inelástica entre dois corpos?
(a) O momento linear de cada corpo se conserva
(b) A energia cinética de cada corpo se conserva
(c) O momento linear do sistema se conserva, mas a energia cinética do sistema não se conserva
(d) O momento linear do sistema não se conserva
(e) A energia cinética do sistema se conserva, mas o momento linear do sistema não se conserva
Ver solução completaQuestão 87
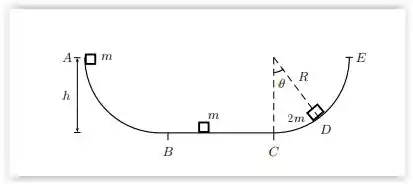
A figura mostra um circuito ABCDE de atrito desprezível, com um trecho horizontal BC, um arco de círculo CE de raio R e o ponto A a uma altura h do trecho horizontal. Um bloco de massa m é abandonado em repouso no ponto A e um bloco idêntico está em repouso sobre o circuito entre B e C. O bloco abandonado em A sofre uma colisão perfeitamente inelástica, com os blocos permanecendo unidos após a colisão. Calcule:
- a velocidade do bloco abandonado em A imediatamente antes de colidir com o outro bloco;
- a velocidade do conjunto imediatamente depois da colisão;
- a velocidade do conjunto no ponto D, onde a direção da normal faz um ângulo θ = 60◦ com a vertical (Supondo que a altura h seja suficiente para que os blocos passem por esse ponto com velocidade não nula);
- o valor da força normal que age sobre os dois blocos grudados, no ponto D.
Questão 88
Uma pessoa quer derrubar um pino de boliche atingindo-o com uma bola. Esta pessoa tem duas bolas de tamanhos e massas iguais, uma feita de borracha e outra de massa. A bola de borracha quica, enquanto a bola de massa gruda no pino. Qual bola seria melhor para derrubar o pino de boliche?
a) borracha
b) massa
c) qualquer uma delas
d) preciso de mais informação
e) nenhuma delas
Ver solução completaQuestão 89
Em uma colisão unidimensional, uma partícula de massa colide com uma partícula de massa em repouso. Se as partículas permanecerem juntas após a colisão, que fração da energia cinética inicial é perdida durante a colisão?
a)
b)
c)
d)
e)
Ver solução completaQuestão 90
Considere uma partícula de massa se movendo com uma velocidade desconhecida . Essa partícula sofre uma colisão com uma segunda partícula de massa inicialmente em repouso, permanecendo ambas as massas unidas depois da colisão, com uma velocidade . Chame essa nova partícula de .
a) Calcule o valor de
b) Calcule a variação de energia cinética dessa colisão
Essa nova partícula colide com uma terceira partícula de massa inicialmente em repouso. Imediatamente após a colisão, a velocidade da partícula é .
c) Calcule os momentos lineares da partícula e da partícula , imediatamente após a colisão: e
d) Calcule as energias cinéticas do sistema composto pelas partículas e , imediatamente antes e imediatamente antes e imediatamente depois da segunda colisão: e . Essa colisão foi elástica ou inelástica?
Ver solução completa



