Um automóvel de massa percorre, em sentido anti-horário, uma pista circular horizontal de raio , com velocidade escalar constante. Conforme será visto no cap. 12, o momento angular de uma das rodas do carro em relação ao centro de massa da roda é dado por , onde é a velocidade angular da roda e é o seu momento de inércia em relação ao CM, que identificamos com o centro da roda. Determine, em módulo, direção e sentido, os vetores momento angular interno, momento angular externo (orbital) e momento angular total da roda em função de , , , e do raio da roda.
Passo 1
Bom, galera, vamos por partes. Primeiro, vamos olhar o vetor do momento angular externo. Estamos falando de um carro numa pista, né? Então a gente vai considerar ele como um ponto! O momento angular pode ser calculado por:
Mas o pode ser relacionado com a velocidade tangencial, já que o movimento na pista é circular, e o momento de inércia do ponto a gente sabe calcular! Fica assim, ó:
Sacou? Logo,
Aqui, o vetor que liga o centro ao carro é paralelo à pista, e a velocidade é paralela à pista e ortogonal ao primeiro. Então, pela regra da mão direita, o momento angular é vertical pra cima!
Passo 2
Agora, vamos olhar o momento angular do ponto localizado bem na extremidade do raio da roda. Da mesma forma, é um ponto girando em torno de um círculo! Podemos fazer igualzinho ao passo .
Aqui, o vetor que liga o centro da roda é perpendicular à pista, e a velocidade é paralela à pista e ortogonal ao primeiro. Então, pela regra da mão direita, o momento angular aponta para o centro da pista!
Passo 3
Beleza! Agora como a gente vai achar o momento total?
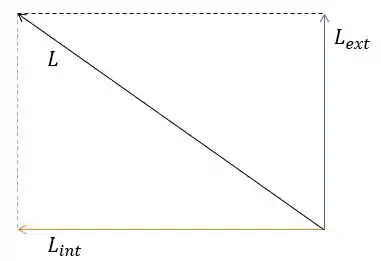
É uma soma de vetores perpendiculares, não é? Então é só a gente chamar o nosso amigão Pitágoras pra ajudar!
Ele vai estar numa direção que faz um ângulo com a vertical, tal que:
Fechou!