Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.6 - Ex. 47
Uma barra de metal delgada e uniforme que tem 2,0 m de comprimento e pesa 90,0 N está suspensa verticalmente do teto por um pivô com atrito desprezível. De repente, ele é atingido num ponto que está 1,50 m abaixo do teto por uma pequena bola de 3,0 kg, movendo-se inicialmente, no sentido horizontal a 10,0 m/s. A bola rebate na direção contrária com uma velocidade escalar de 6,0 m/s.
a) Calcule a velocidade escalar angular da barra logo após a colisão.
b) Durante a colisão, por que o momento angular se conserva, mas o momento linear não?
Passo 1
Para a resolução do problema, vamos aplicar a conservação de momento:
O momento de inércia da barra é .
O sistema pode ser representado da seguinte forma:
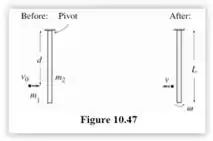
Com isso, teremos
Passo 2
O momento angular é conservado quando o torque resultante que atua sobre um sistema é igual a zero. Além disso, os torques das forças internas podem transferir momento angular de uma parte para outra do corpo.
Neste problema, não há torques desequilibrados sobre o pivô, portanto o momento angular é conservado.
O momento de linear é quem mede o grau em que um objeto resiste aceleração de rotação em torno de um eixo. O pivô exerce uma força externa horizontal desequilibrada no sistema, por isso o momento linear não é conservado.
Resposta
a);
b) O momento linear não é conservado, pois o pivô exerce uma força externa horizontal desequilibrada no sistema.