Um bloco está apoiado em um êmbolo que se move verticalmente em um movimento harmônico simples. (a) se o MHS tem um período de , para que valor da amplitude do movimento o bloco e o êmbolo se separam? (b) Se o êmbolo se move com uma amplitude de , qual é a maior frequência para a qual o bloco e o êmbolo permanecem continuamente em contato?
Passo 1
Show de bolinhas pessoal, tudo beleza?
Esse problema aqui é o seguinte: como a questão fixou um período , se a gente aumentar demais a amplitude do movimento, o bloco em MHS vai precisar de uma aceleração muito alta pra percorrer ela em um segundo! Olha esse desenho em que o bloco perde contato quando o êmbolo começa a descer:
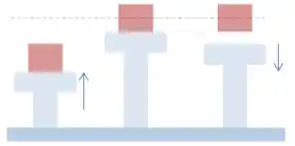
É como se você estivesse em um elevador subindo muito rápido, e de repente ele muda a direção e começa a descer rápido também: você ia perder o contato com o chão e talvez bater de cabeça no teto!
Agora vamos tentar fazer isso matematicamente. Temos que descobrir qual é a condição que faz o bloco perder contato com o êmbolo.
Passo 2
Como o bloco não está “grudado” no êmbolo, qual pode ser a aceleração máxima do bloco assim que o êmbolo começa a descer?
Exatamente, é a aceleração de queda livre mesmo, ou seja, . Se o êmbolo frear e descer com uma aceleração maior do que (puxado por alguma força lá embaixo), ele vai deixar o bloco pra trás.
Ou seja, a condição pra que não haja perda de contato é:
Onde é o módulo da aceleração máxima que o êmbolo atinge. Essa é uma fórmula que nós conhecemos:
Em que é a frequência angular do oscilador, e é a amplitude.
Passo 3
(a) Podemos achar a frequência angular através do período:
E substituindo na fórmula:
E esse é o valor máximo que a amplitude pode ter sem que haja perda de contato.
Passo 4
(b) Agora a única diferença é que ao invés de fixar o período, a questão fixou a frequência. Vamos voltar na mesma fórmula de antes:
Só que agora vamos trocar o período pela frequência usando:
Como a frequência é um valor positivo:
Prontinho!
Resposta
(a) O bloco e o êmbolo se separam quando
(b)