Exercícios de Introdução ao MHS - Lista de Exercícios Resolvida
Questão 1
Qual é a aceleração máxima de uma plataforma que oscila com uma amplitude de e uma frequência de ?
Ver solução completaQuestão 2
Uma partícula descreve um movimento harmônico simples de período e amplitude de . O módulo de sua velocidade ao passar por um ponto de trajetória cuja elongação é vale:
Questão 3
Uma partícula com massa de descreve um movimento harmônico simples com um período de e uma velocidade máxima de . Calcule:
(a) a frequência angular.
(b) o deslocamento máximo da partícula.
Ver solução completaQuestão 4
Um objeto que executa um movimento harmônico simples leva 0,25 s para se deslocar de um ponto de velocidade nula para o ponto seguinte do mesmo tipo. A distância entre esses pontos é 36 cm. Calcule:
(a) o período.
(b) a frequência.
(c) a amplitude do movimento
Ver solução completaQuestão 5
A função: descreve o movimento harmônico simples de um corpo. Em , quais são:
- O deslocamento.
- A velocidade.
- A aceleração.
- A fase do movimento.
- A frequência.
- O período.
Questão 6
Qual das seguintes afirmações é verdadeira sobre um objeto executando um movimento harmônico simples?
- A velocidade do objeto nunca é zero.
- A aceleração do objeto nunca é zero,
- A velocidade e a aceleração do objeto são simultaneamente zero.
- A velocidade do objeto é zero quando sua aceleração é máxima.
- A aceleração máxima do objeto é igual a sua velocidade máxima.
Questão 8
Uma partícula descreve um movimento harmônico simples de período e amplitude de . O módulo de sua velocidade ao passar por um ponto de trajetória cuja elongação é vale:
Questão 9
Um objeto de massa m oscila em um movimento harmônico simples. Sabendo-se que a distância máxima em relação ao ponto de equilíbrio é dada por A, que o período é T e que no instante t=0 o objeto está na origem, x=0, mas movendo-se na direção –x, mostre que (Obs: Estas equações são válidas para qualquer Oscilador Harmônico Simples):
- A equação do movimento pode ser dada por
Questão 10
Quando deslocados da posição de equilíbrio, os dois átomos da molécula de são submetidos a uma força restauradora do tipo F = - kx com a constante k = 580 N/m. Calcule a frequência de oscilação da molécula de . Obs: busque na literatura os dados que você precisará usar para resolver o problema.
Ver solução completaQuestão 11
Um bloco de massa desliza sem atrito sobre um plano inclinado que faz um ângulo com a horizontal e tem uma mola fixa no final da rampa. O bloco é solto de uma posição inicial tal que a distância entre a ponta livre da mola e a face do bloco é . Quando o bloco bate na mola, um dispositivo é acionado conectando o bloco na mola. O bloco comprime a mola até um valor máximo igual a , quando a velocidade instantânea do bloco torna-se zero. Considere um eixo ao longo do plano inclinado no sentido descendente e com sua origem na posição da ponta livre da mola quando ela não está deformada. Determine, em função dos parâmetros fornecidos e da aceleração da gravidade no local:
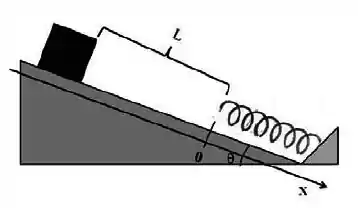
- A frequência angular do movimento harmônico simples que o bloco executa após conectar-se à mola.
- A posição na qual a velocidade do bloco é máxima.
- A posição mais alta que o bloco alcança após conectar-se à mola.
Questão 12
Qual das seguintes afirmações é verdadeira a respeito de um objeto que está executando um movimento harmônico simples?
(A) A velocidade do objeto nunca é zero.
(B) A aceleração do objeto nunca é zero.
(C) A velocidade e a aceleração do objeto se anulam simultaneamente.
(D) A velocidade do objeto é máxima quando sua aceleração é zero.
E) A velocidade e a aceleração do objeto são máximas simultaneamente.
Ver solução completaQuestão 13
Um oscilador harmônico simples pode ser descrito pela seguinte equação diferencial: . Considere as seguintes equações abaixo, onde A, e são constantes, e verifique se elas descrevem um movimento MHS.
a )
b)
c)
Ver solução completaQuestão 14
Uma corda é acionada por um gerador de ondas que estica a corda em uma direção perpendicular à corda, conforme apresentado na figura. A função de onda para a onda estacionária em uma corda, fixa em ambas as extremidades, é dada por , onde e estão em centímetros e está em segundos. Determine:
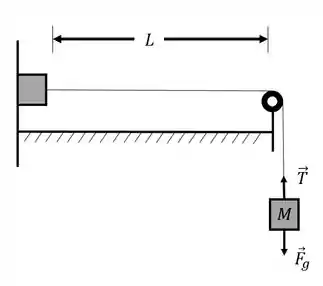
- O número de onda e o comprimento de onda das ondas da onda estacionária
- A frequência e a velocidade das ondas na corda
- O comprimento da corda, sabendo que a corda vibra em seu quarto harmônico
- Represente a onda estacionária, indicando a posição de cada nó. Considere a onda no instante e os extremos da corda em e
Questão 15
O deslocamento de um objeto oscilando em movimento harmônico simples é descrito pela equação . Se e é negativo, então a constante de fase é
Questão 16
Um bloco realiza um movimento harmônico simples. Se tanto o período quanto a amplitude do movimento são dobrados, o que ocorre com a máxima velocidade?
(a) Aumenta em 4 vezes.
(b) Cai pela metade.
(c) Dobra.
(d) Permanece inalterada.
(e) Diminui em 1/4.
Ver solução completaQuestão 17
Uma partícula se move segundo um movimento harmônico simples. Quando sua posição é , o modulo de sua velocidade é
Questão 18
Qual das seguintes afirmações é verdadeira sobre um objeto executando um movimento harmônico simples?
- A velocidade do objeto nunca é zero;
- A aceleração do objeto nunca é zero;
- A velocidade e a aceleração do objeto são simultaneamente zero;
- A velocidade do objeto é zero quando sua aceleração é máxima;
- A aceleração máxima do objeto é igual à sua velocidade máxima.
Questão 19
A agulha de uma máquina de costura executa movimento harmônico simples com amplitude de e frequência de . Responder justificando:
- Qual é a velocidade máxima da agulha?
- Qual é a aceleração máxima da agulha?
Questão 20
O gráfico apresentado mostra a elongação em função do tempo para um movimento harmônico simples.
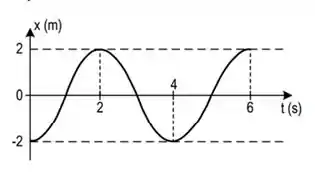
Qual a equação correspondente nas unidades indicadas no gráfico?
- ]
- ]
- ]
- ]
Questão 21
A posição de um objeto que descreve um movimento harmônico simples é dada por
(em unidades SI).
Quais são, respectivamente, os valores da velocidade máxima e da aceleração máxima deste objeto?
(A) e
(B) e
(C) e
(D) e
(E) e
Ver solução completaQuestão 22
Um corpo de massa igual a 4kg foi preso à extremidade de uma mola, com k = 16N/m, a amplitude de oscilação foi igual a 0,05m. O conjunto oscilou durante um certo tempo (movimento harmônico simples), podemos afirmar que a velocidade máxima de oscilação foi igual a:
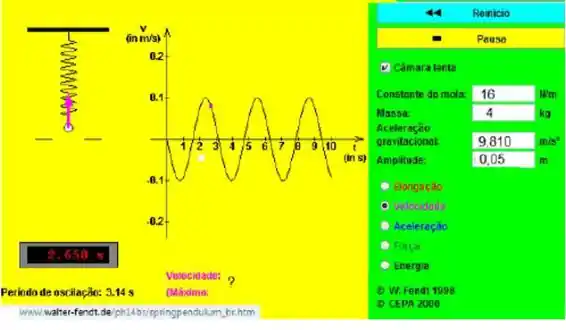
Questão 23
Um oscilador harmônico simples, oscila com amplitude A, tendo frequência , e energia mecânica . Num segundo momento oscila com frequência , amplitude 2A e energia mecânica . Indique a opção verdadeira.
- e
- e
- e
- e
- e
Questão 24
Um objeto que executa um movimento harmônico simples leva para se deslocar de um ponto de velocidade nula para o ponto seguinte do mesmo tipo. A distância entre os pontos é de . Calcule o período, a frequência e a amplitude do movimento.
Ver solução completaQuestão 25
A função descreve o movimento harmônico simples de um corpo. No instante , determine o deslocamento, a velocidade, a aceleração e a fase do movimento. Qual é a frequência e qual o período do movimento?
Ver solução completaQuestão 26
Um oscilador é formado por um bloco com uma massa de ligado a uma mola. Quando é posto em oscilação com uma amplitude de , o oscilador repete o movimento a cada . Determine o período, a frequência, a frequência angular, a constante elástica, a velocidade máxima e o módulo da força máxima que a mola exerce sobre o bloco.
Ver solução completaQuestão 27
Os objetos A e B estão presos, separadamente, a uma mola ideal e executam movimento harmônico simples. O período e a amplitude do movimento do objeto B são duas vezes maiores que os valores correspondentes do objeto A. Qual é a relação entre as velocidades máximas dos dois objetos?
- a velocidade de B é duas vezes maior do que a de A;
- a velocidade de B é quatro vezes maior do que a de A;
- a velocidade de A é duas vezes maior do que a de B;
- a velocidade de A é quatro vezes maior do que a de B;
- as velocidades máximas dos objetos A e B são iguais;
Questão 28
Um pêndulo constituído de uma esfera presa a um fio de comprimento é solto de uma posição , a partir do repouso. Considerando a aproximação para a validade do movimento harmônico simples mostre que a velocidade do pêndulo ao passar por pode ser calculada por . Usando a conservação da energia encontre essa velocidade exatamente para um ângulo qualquer (não somente para pequeno ângulo!!) e mostre que seu resultado está de acordo com o resultado do item quando for pequeno. Encontre a diferença entre o valor aproximado e o valor exato para e . Encontre a diferença ente o valor aproximado e o valor exato para e . Compare os resultados dos itens e . O que você conclui?
Ver solução completaQuestão 29
A amplitude e a constante de fase de um oscilador harmônico simples (sistema massa-mola com e conhecidos) são determinadas
(A) pela frequência
(B) pela massa e pela constante elástica
(C) exclusivamente pelo deslocamento inicial
(D) exclusivamente pela velocidade inicial
(E) pelo deslocamento inicial e pela velocidade inicial
Ver solução completaQuestão 31
Um pêndulo simples executa oscilações de pequena abertura angular de modo que a esfera pendular realiza um M.H.S.
Assinale a opção correta:
- o período de oscilação é proporcional ao comprimento do pêndulo.
- o período de oscilação independe do comprimento do pêndulo.
- o período de oscilação é inversamente proporcional ao valor da aceleração da gravidade local.
- o período de oscilação independe do valor da aceleração da gravidade local.
- o período de oscilação independe da massa da esfera pendular.
Questão 32
O diapasão é um dispositivo utilizado pelos músicos na afinação de instrumentos musicais. O diapasão executa movimento harmônico simples?
Ver solução completaQuestão 33
Uma bola de aço está pendurada em uma mola ideal vertical e descreve um movimento harmônico simples com amplitude de 0,1 m e uma frequência angular de rad/s. Qual das expressões abaixo representa a aceleração da bola, em , em função do tempo?
a)
b)
c)
d)
e)
Ver solução completaQuestão 34
Uma criança coloca um pouco de areia dentro de uma garrafa de refrigerante vazia e a põe para boiar em um tanque com água. Podemos supor que a garrafa tem seção reta uniforme de área , sendo muito menor que a área do tanque, de forma que o movimento da água do tanque possa ser desprezado. A massa total da garrafa, incluindo a areia, vale . A densidade da água é . No equilíbrio, a parte submersa da garrafa tem comprimento . A criança força a garrafa para baixo uma pequena distância além da posição de equilíbrio, e a solta. Considerando que a garrafa tenha apenas movimento vertical, a frequência angular de suas oscilações em torno do equilíbrio vale:
Questão 35
Sobre a superfície muito lisa de uma mesa se encontra uma mola, cuja a constante é de . Uma das extremidades da mola está fixada na mesa e na outra está presa um bloco de que também repousa sobre a mesa. Um outro bloco (também de ) desloca sobre a superfície com velocidade de e colide com o bloco preso à mola. Após a colisão, os dois blocos permanecem grudados um no outro e o sistema começa a oscilar. Considerando e no instante da colisão, encontre a equação do movimento harmônico resultante.
Ver solução completaQuestão 36
Num movimento harmônico simples, a rapidez é máxima quando
(A) o módulo da aceleração é máximo.
(B) o módulo da aceleração é mínimo.
(C) o deslocamento é máximo.
(D) a energia potencial é máxima.
(E) a energia cinética é mínima.
Ver solução completaQuestão 37
Quando se quadruplica a amplitude de um oscilador harmônico, sua velocidade máxima:
- Dobra
- Cai à metade
- Permanece a mesma
- Se reduz à ¼
- quadruplica
Questão 38
(Cap 13 - Ex 13) A ponta da agulha de uma máquina de costura se move com MHS ao longo de um eixo com uma frequência igual a . Em os componentes da posição e da velocidade são respectivamente, e . Ache o componente da aceleração da agulha para . Escreva equações para os componentes da posição, da velocidade e da aceleração do ponto considerado em função do tempo.
Ver solução completaQuestão 39
Uma massa ligada a uma mola tem posição instantânea , com em centímetros e em segundos. A velocidade da massa é a metade da sua velocidade inicial no instante:
Questão 40
(Cap 13 - Ex 27) Você observa um objeto movendo-se em . Quando o objeto é deslocado até a direita da sua posição de equilíbrio, sua velocidade é igual a para a direita, e sua aceleração é igual a para a esquerda. A que distância máxima desse ponto irá o objeto se mover antes de parar momentaneamente e depois recomeçar a se mover para a esquerda?
Ver solução completaQuestão 41
Um oscilador harmônico simples tem amplitude , atinge velocidade máxima de e
possui aceleração máxima . Num dado instante de tempo, qual das opções abaixo pode
representar sua posição, sua velocidade e sua aceleração, respectivamente?
(a) , , .
(b) , , .
(c)
(d) , , .
(e) , , .
(f) , , .
(g) , , .
(h) Nenhuma das alternativas anteriores.
Ver solução completaQuestão 42
A figura ao lado mostra o deslocamento de um bloco preso a uma mola executando uma movimento harmônico simples. Qual é o módulo da velocidade máxima que o bloco pode ter? A resposta deve estar na unidade
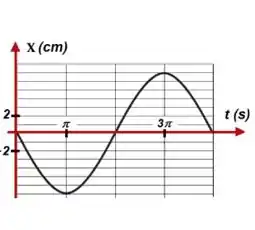
Questão 43
Uma das frequências harmônicas de uma certa corda sob tensão é . A frequência harmônica seguinte é . Qual é a frequência harmônica, em , que se segue à de ?
- 200
- 260
- 320
- 380
- 440
Questão 44
Uma partícula está em movimento harmônico simples com período . No instante , a partícula passa pela posição de equilíbrio. Em qual dos instantes abaixo a partícula estará mais afastada da posição de equilíbrio?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 45
Observando o gráfico do MHS abaixo podemos dizer que é descrito pela função
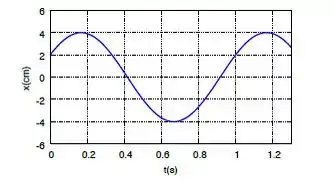
Questão 46
Uma corda de comprimento e densidade , com ambas as extremidades fixas, oscila no quarto harmônico de uma onda estacionária de acordo com a seguinte equação:
onde numa das extremidades da corda ( é dado em metros e em segundos).
Qual o comprimento da corda?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 47
Quando se quadruplica a amplitude de um oscilador harmônico:
- Sua velocidade máxima dobra.
- Sua velocidade máxima cai à metade.
- Sua velocidade máxima fica inalterada.
- Sua velocidade máxima fica reduzida a .
- Sua velocidade máxima quadruplica.
Questão 48
Vários tipos de movimento foram estudados em Física teórica, sempre caracterizados por seus parâmetros físicos ou matemáticos. Considerando uma partícula que descreve uma trajetória circular com velocidade angular constante e a projeção ortogonal desta partícula sobre o diâmetro da circunferência descrita, PODEMOS DIZER que o movimento da projeção sobre o diâmetro é um:
- Movimento retilíneo uniformemente retardado.
- Movimento harmônico simples.
- Movimento retilíneo uniformemente acelerado.
- Movimento harmônico acelerado.
- Movimento retilíneo uniforme.
