Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.3 - Ex. 23

Uma bola maciça é liberada do repouso e desliza para baixo pela encosta de uma colina com inclinação de 65,0 ° com o plano horizontal. a) Qual valor mínimo deve o coeficiente de atrito estático entre as superfícies da colina e da bola ter para que nenhum deslizamento ocorra? b) O coeficiente de atrito calculado no item (a) é suficiente para impedir que uma bola oca (como uma bola de futebol) deslize? Justifique sua resposta. c) No item (a), por que usamos o coeficiente de atrito estático e não o coeficiente de atrito cinético?

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que uma bola maciça é liberada do repouso e desliza para baixo pela encosta de uma colina com inclinação de 65,0 ° com o plano horizontal.

Queremos encontrar o valor mínimo deve o coeficiente de atrito estático entre as superfícies da colina e da bola ter para que nenhum deslizamento ocorra.

Com o valor que a gente encontrar, devemos indicar se vai ser suficiente para impedir que uma bola oca deslize.

Por fim, devemos explicar o porquê que utilizaremos o coeficiente de atrito estático e não o cinético.

Bom... para resolver isso, precisaremos esboçar o diagrama de corpo livre para analisarmos as forças.

Precisaremos de outros conceitos que serão apresentados no Passo 2.

Passo 2

Precisaremos da segunda lei de Newton, ou seja:

F = m a

Onde F é a força, m é a massa e a é a aceleração.

E também da forma análoga da segunda lei de Newton para a rotação da polia, ou seja:

τ = I α

Onde τ é o torque, I é o momento de inércia e α é a aceleração angular.

Agora bora aplicar!! 😉

Passo 3

  1. Bom... vamos começar esboçando o diagrama de corpo livre e aplicando a segunda lei de Newton para entender o problema:

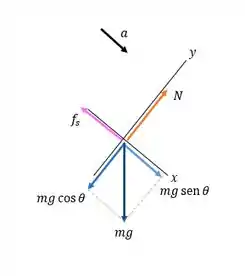
    2. Repara que a bola desce pelo eixo x , pois a a força normal N está perdedicular a esse eixo no sentido de + y . A força peso foi decomposta em seno e cosseno. Então ficamos assim,

    No e i x o   y :

    ∑ F y = m a y

    N = m g cos ⁡ θ

    E

    f s = μ s m g cos ⁡ θ

    Onde g é a aceleração da gravidade e μ s é o coeficiente de atrito estático.

    No e i x o   x :

    ∑ F x = m a x

    m g sen ⁡ θ - μ s m g cos ⁡ θ = m a

    ⇒ a = g ( sen ⁡ θ - μ s cos ⁡ θ )   ( e q u a ç ã o   1 )

    Vamos continuar entendo o problema!

    Passo 4

    Então, vamos desenhar um diagrama de corpo livre para a bola:

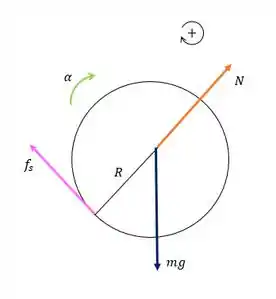
    A N e a força m g atuam no centro da bola e não fornece torque.

    Então, ∑ τ = τ f = μ s m g cos ⁡ θ R ;

    I = 2 5 m R 2

    Então, aplicando ∑ τ = I c m α . Implica em:

    α = a R

    Então,

    μ s g cos ⁡ θ = 2 5 a   ( e q u a ç ã o   2 )

    Passo 5

    Temos duas equaçõese nas duas incógnitas a e s μ s .

    Isso implica que:

    a = 5 7 g sen ⁡ θ

    E então,

    μ s = 2 7 tan ⁡ θ = 2 7 tan ⁡ 65 ° = 0,613

    Passo 6

  2. Repetindo os cálculos do item (a), mas agora para I = 2 3 m R 2 e a = 3 5 g sen ⁡ θ .

    3. Então,

    μ s = 2 5 tan ⁡ θ = 2 5 tan ⁡ 65 ° = 0,858

    O valor de μ s calculado na parte (a) não é grande o suficiente para evitar escorregões na esfera oca.

    Passo 7

  3. Não há escorregões no ponto de contato.

É necessário mais atrito para uma bola oca, pois para uma bola dado m e R , ele tem um I   maior e é necessário mais torque para fornecer o mesmo   α .

Observe que   μ s necessário é independente da massa ou raio da bola e depende apenas de como essa massa é distribuída.

Resposta

  1. μ s = 0,613
  2. Não.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9.13P Uma haste homogênea de comprimento L equilibra-se inicialmente na vertical, apoiada em uma de suas extremidades sobre uma superfície plana horizontal. Um pequeno impulso faz com que a haste caia
9.1E Calcule o resultado das operações R y π 2 R z π 2 e R z π 2 R y π 2 sobre o dado da Figura 9.15. Nota: o produto de operações AB significa operação B seguida de operação A. Portanto, R y π 2 R z
9.18P Calcule a aceleração linear do ioiô considerado no Exemplo 9.6.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
10.8P Na figura 10.12, o cabo rola na roldana sem deslizamento. Calcule a aceleração angular da roldana.