Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 93

Calculamos, no texto, o alcance de um projétil que cai no mesmo nível de onde foi lançado e encontramos R = v 0 2 g sin ⁡ 2 θ , Uma bola de golfe recebe uma tacada inicial de 45,0 m/s a um ângulo de 35° e cai na grama 20 m abaixo do ponto da tacada. (a) Calcule o alcance, usando a equação R = v 0 2 g sin ⁡ 2 θ , mesmo a bola tendo sido lançada de um ponto mais elevado. (b) Mostre que o alcance, no caso mais geral é dado por: R = v 0 2 2 g sin ⁡ 2 θ 1 + 1 - 2 g y v 0 2 sin 2 ⁡ θ , onde y é a altura da grama em relação ao ponto de lançamento, isto é, y = - h . (c) Calcule o alcance usando esta fórmula . Qual é o erro percentual ao ignorar o desnível?

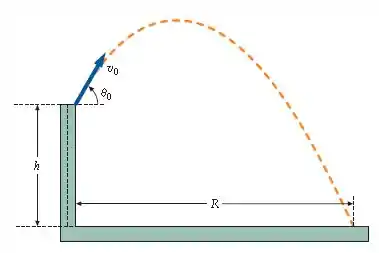
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O alcance máximo para um mesmo nível é dado por:

R = v 0 2 g sin ⁡ 2 θ

R = 45 2 9,81 sin ⁡ 2 ⋅ 35 °

R = 194   m

Passo 2

O alcance máximo é dado contendo um desnível é dado por:

x - x 0 = v 0 x t + 1 2 a x t 2

Sabemos que a posição inicial é x 0 = 0 e que a aceleração é nula, temos:

x = v 0 x t

x = ( v 0 cos ⁡ θ ) t

t = x v 0 cos ⁡ θ

Analisando a posição verticalmente, temos:

y - y 0 = v 0 y t + 1 2 a y t 2

Sabemos que a posição inicial y 0 = h e que a aceleração é a da gravidade para baixo, logo:

y = h + v 0 y t - 1 2 g t 2

y = h + ( v 0 sin ⁡ θ ) t - 1 2 g t 2

Relacionando as duas equações da posição, temos:

y = h + ( v 0 sin ⁡ θ ) x v 0 cos ⁡ θ   - 1 2 g x v 0 cos ⁡ θ 2  

y = h + ( x tan ⁡ θ )   - 1 2 g x v 0 cos ⁡ θ 2

Aplicando ao movimento, temos que:

0 = h + ( R ⋅ tan ⁡ θ )   - 1 2 g R v 0 ⋅ cos ⁡ θ 2

R = v 0 2 2 g sin ⁡ 2 θ 1 + 1 + 2 g h v 0 2 sin 2 ⁡ θ

Como sabemos que h = - y , podemos dizer que:

R = v 0 2 2 g sin ⁡ 2 θ 1 + 1 - 2 g y v 0 2 sin 2 ⁡ θ

Passo 3

O alcance calculado com o desnível será:

R = 45 2 2 ⋅ 9,81 sin ⁡ 2 ⋅ 35 ° 1 - 1 + 2 ⋅ 9,81 ⋅ ( - 20 ) 45 2 sin 2 ⁡ 35 °

R = 219   m

Existe um erro e ele é dado por:

% e r r o = R - R 1 R

% e r r o = 219 - 194 219

% e r r o = 11 %

Resposta

a ) R = 194   m

c ) R = 219   m

% e r r o = 11 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jogador de futebol americano faz um lançamento (manual) a um ângulo de 36,5° acima da horizontal, em um ponto distante 3,50 m do ponto de onde partiu, 2,50 s antes, aquele que deve receber o passe.
Em uma partida de beisebol, o monte do arremessador fica 0,20 m acima do nível do campo e a 18,4 m da base. Um arremessador atira uma bola com uma rapidez inicial de 37,5 m/s. No momento em que a bola
Galileu mostrou que, se os efeitos da resistência do ar são ignorados, os alcances de projéteis (no mesmo nível) cujos ângulos de projeção diferem de 45°, para mais e para menos, do mesmo valor, são i
Se você pode atirar uma bola a uma distância horizontal máxima L, quando no nível do chão, a que distância você pode atirar a bola do alto de um edifício de altura h, se você a atira a (a) 0 ° , (b) 3
Dentro do carro, um motorista atira verticalmente para cima um ovo, que atinge uma altura máxima justo abaixo do teto, 65 cm acima do ponto de lançamento. Ele recupera o ovo na mesma altura de lançame