Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 46

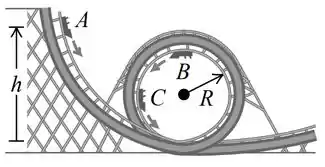
Um carro em um parque de diversões se desloca sem atrito ao longo do trilho indicado na Figura 7.32. Ele parte do repouso no ponto A situado a uma altura h acima da base do círculo. Considere o carro como uma partícula. a) Qual é o menor valor de h (em função de R ) para que o carro atinja o topo do círculo (ponto B) sem cair? b) Se h   = 3,50 R e R   =   20,0   m , calcule a velocidade, o componente radial da aceleração e o componente tangencial da aceleração dos passageiros quando o carro está no ponto C, que está na extremidade de um diâmetro horizontal. Use um diagrama aproximadamente em escala para mostrar esses componentes da aceleração.

Passo 1

Pela segunda lei ∑ F → = m   a → , temos que a aceleração centrípeta dada por a = v 2 R   onde   v se torna v = g R . Assim vamos utilizar o princípio da conservação de energia para determinar qual deve ser a altura mínima que h deve possuir para que o carro não caia.

  1. Aplicando a conservação de enrgia em dois pontos, A e B, que são respsctivamente a base e o topo do círculo, temos que

    2. E A = E B

    Como o carro parte do repouso, temos que K A = 0 , assim como U A = m g h pois tomamos o chão como referêncial.

    Para a energia no ponto B temos

    E B = K B + U B

    Assim teremos que

    m g h = m v B 2 2 + m g 2 R = m g R 2 + m g 2 R = 5 2 m g R

    Implicando que

    h   = 5 2 R

    Desta forma dizemos que a altura mínima que h deve ter é de 5 2 R .

    Passo 2

  2. Usando a relação

m g h = m v C 2 2 + m g h c

E assumindo h   =   3,50   R   e R = 20,0   m como sugerido no enunciado, e ainda tomando h c = R, visto que ele está em uma das extremidades , temos que

v C = 2 g [ 3,50 R - R ] =   2 g R [ 2,50 ] 5 ⋅ 9,80 m s 2 ⋅ ( 20,0   m ) = 31,3   m s  

Passo 2

Ainda para o item b, temos que a aceleração centrípeta é dada por:

a c = v c 2 R = 49,0   m s 2

Prontinho!

Resposta

  1. h > 5 2 R
  2. v C = 31,3   m s e a c = v c 2 R = 49,0   m s 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

34 . || De cima do muro de 10m de altura de uma fortaleza, um canhão inclinado em 30° acima da horizontal dispara uma bala com 80m / s . Qual será o módulo da velocidade da bala no solo?
33 . | Você dirige a 35k m / h quando a estrada subitamente desce 15m em direção a um vale. Você tira o pé do acelerador e desce em ponto morto para o vale. Exatamente quando atinge o fundo do vale, v
36 . || Um cubo de gelo bem liso desliza dentro de um tubo horizontal liso com 20c m de diâmetro interno, descrevendo uma trajetória em um plano vertical. Na parte mais inferior do tubo, a velocidade
35 . || O Frisbee de seu amigo ficou preso em uma árvore a 16m acima do solo. Você deseja desalojá-lo acertando-o com uma pedra. O brinquedo está firmemente preso à árvore, de modo que você percebe qu
42 . || Um pacote de massa m é liberado a partir do repouso do galpão de armazenamento de uma loja e desliza sem atrito por uma rampa até o caminhão estacionado. Infelizmente, o motorista estacionou o