Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 81
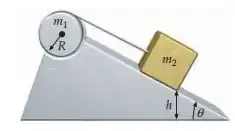
Um cilindro uniforme de massa e raio gira sobre suportes sem atrito. Um fio sem massa, enrolado em torno do cilindro, está ligado a um bloco de massa , que está sobre um plano inclinado de , sem atrito, como mostrado na figura. O sistema é largado do repouso quando o bloco está a uma distância vertical da base do plano inclinado. (a) Qual é a aceleração do bloco? (b) Qual é a tensão no fio? (c) Qual é a rapidez do bloco quando ele chega à base do plano inclinado? (d) Determine suas respostas para o caso especial em que e . Suas respostas são o que você esperaria neste caso especial? Explique.
Passo 1
a) Oláaa, querido! Cê tá bem?
Então, a gente tem um objeto preso a um cilindro por uma corda. Quando o objeto é largado do repouso, esse movimento desse objeto faz com que o cilindro gire, ou seja, que ela tenha uma aceleração angular.
Ele pede a aceleração do objeto. Cara, como ele pede aceleração e temos várias forças envolvidas é uma boa a gente usar a segunda lei de Newton, ok?
E falou de usar a segunda lei de Newton, a gente pensa logo em fazer os diagramas de corpo livre da esfera e do objeto. Ficam assim:
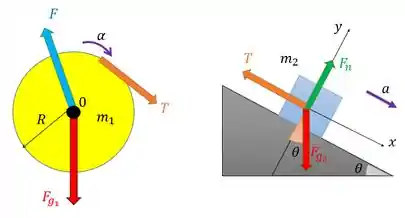
Essa tá um pouco inclinada porque a força que o suporte faz para segurar o cilindro, tá? E a gente colocou os sentidos positivos como sendo no sentido da aceleração.
Agora vamos achar !
Passo 2
Percebe que a tensão no cilindro é a única força nele que não passa pelo seu centro, então ela é a única responsável por fazer o cilindro girar, já que ela vai causar um torque no cilindro.
E se o cilindro está girando, a gente pode usar a segunda lei de Newton para rotação nele. Ela tem essa carinha:
A única força gerando o torque é a tensão . Ela é perpendicular ao raio do cilindro, então o torque gerado vai ser , aí nossa lei de Newton fica:
E é o momento de inércia do cilindro com relação a um eixo que passa pelo seu centro. Ele tem essa fórmulinha:
Substituindo:
Lembra como relacionamos aceleração angular e tangencial ? Assim oh:
Substituindo na nossa equação:
Mas a gente não sabe quem é e nem quem é , então precisamos de mais uma equação.
Passo 3
Bora fazer a segunda lei de Newton mais comum para o bloco. Para a direção :
A componente de no eixo é :
Podemos substituir aqui a expressão para que achamos no passo anterior :
Agora é isolar :
Passo 4
b) Queremos a tensão agora. Temos que
Mas a gente acabou de achar , então podemos substituir aí:
Passo 5
c) Queremos a rapidez do bloco no fim da rampa. Ele diz a altura do bloco na posição incial. Isso é a dica master para gente usar conservação de energia.
Inicialmente, o bloco tinha apenas energia potencial gravitacional. Não havia energia cinética porque ele e o cilindro estavam paradinhos. Então temos:
(o cilindro não varia sua altura durante o movimento, então a gente não vai pensar na energia potencial gravitacional dele)
Depois que começa a descer, o bloco adquire energia cinética, e o cilindro energia cinética rotacional.
Substituindo a expressão de cada uma dessas energias:
Passo 6
Aí a conservação fica:
Mas lembra que é o momento de inércia do cilindro e vale . E a gente pode escrever a rapidez angular usando essa expressão:
Percebe que é o mesmo do bloco, porque essa é a velocidade que o movimento do bloco gera na borda do cilindro. Substituindo as nossas expressões de e na conservação:
Isolando :
Dividindo em cima e embaixo por :
Passo 7
d) Para o caso em que e :
A tensão fica
E a rapidez
Realmente, esse é o caso equivalente a não ter polia (, a massa zerada, é a massa da polia). Como o ângulo é , o bloco cairia verticalmente com aceleração , sem interferência da tensão. Aí a conservação de energia seria:
Como encontramos! Então nossos resultados fazem sentido.
Resposta
- , ,