Exercícios de Torque em Polias Não-Ideais - Lista de Exercícios Resolvida
Questão 1
Um cabo ideal está enrolado em volta de uma polia de raio e massa e tem sua outra extremidade ligada a um bloco de . O bloco se encontra apoiado sobre um plano inclinado de em relação a horizontal. O sistema é solto a partir do repouso. Não existe atrito entre o plano e o bloco. Considerando o momento de inércia da polia , calcule:
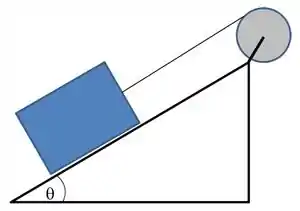
A aceleração angular da polia.
a tração no cabo e o torque na polia.
O módulo da aceleração linear de um ponto na borda na polia após de iniciado o movimento.
Ver solução completaQuestão 2
Dois discos de mesmo raio e de massa diferentes, onde , estão presos ao teto por fios ideais e enrolados em suas bordas. Liberados a partir do repouso eles caem verticalmente onde é o módulo da aceleração local da gravidade; o momento de inércia de um disco em torno do seu eixo de rotação que passa pelo seu centro é igual . Os módulos das trações nos fios em cada disco são e e as acelerações dos seus centros de massa são e , respectivamente, a opção correta abaixo é:
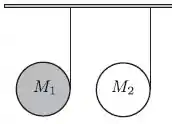
- ;
- e
Questão 3
Considere dois discos um de raio e de massa e outro de raio e de massa unidos concentricamente formando um sistema (disco composto) rígido, cujo momento de inércia vale quando gira livremente em torno do eixo fixo e perpendicular ao plano dos discos passando pelo centro. Duas massas, e , presas a cordas finas e inextensíveis enroladas na periferia dos discos de raios e respectivamente, fazem girar o disco composto quando soltas; considere que é o módulo da aceleração local da gravidade.
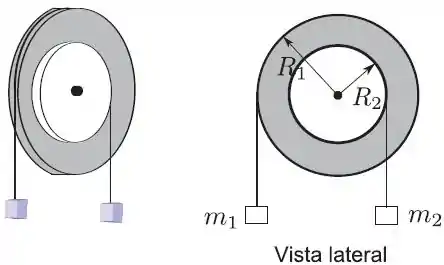
- Isole os blocos e o disco composto e represente em um diagrama de corpo livre todas as forças, identificando-as, que atuam em cada um deles; use como referência a vista lateral do sistema.
- Escreva as equações do movimento de rotação do disco composto e de translação dos blocos.
- Determine a aceleração angular, , do disco composto.
- Determine matematicamente a condição para que o sistema esteja em equilíbrio
Questão 4
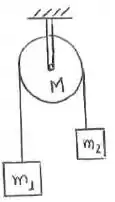
Uma máquina de Atwood possui massas , e uma polia maciça uniforme de massa M =2,0kg. O módulo da aceleração linear da massa vale:
a)
b)
c)
d)
e)
Questão 5
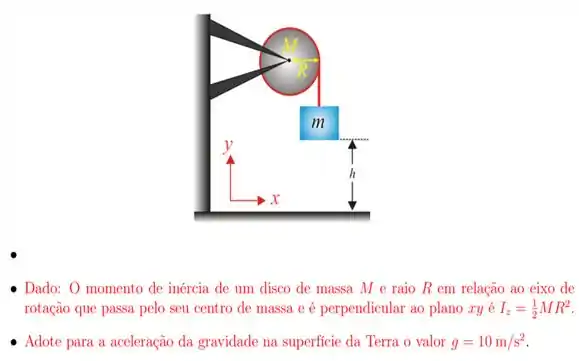
17. Uma polia homogênea, que possui o formato de um disco com raio e massa está fixa em um suporte podendo girar livremente, sem atrito, em volta de um eixo que passa pelo seu centro e é perpendicular ao plano . Uma corda leve (de massa desprezível), que está enrolada nessa polia, prende um bloco de massa , como mostra a figura. À medida que a polia gira, o bloco se movimenta para baixo, sem que a corda escorregue sobre a polia. O sistema é solto do repouso, quando m está a uma altura acima do chão horizontal. O módulo do vetor velocidade com que o bloco de massa m chega ao chão, em metros por segundo, é aproximadamente:
Questão 6
Considere dois discos um de raio e de massa e outro de raio e de massa unidos concentricamente formando um sistema (disco composto) rígido, cujo momento de inércia vale quando gira livremente em torno do eixo fixo e perpendicular ao plano dos discos passando pelo centro. Duas massas, e , presas a cordas finas e inextensíveis enroladas na periferia dos discos de raios e respectivamente, fazem girar o disco composto quando soltas; considere que é o módulo da aceleração local da gravidade.
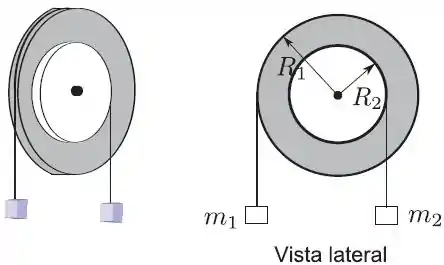
- Isole os blocos e o disco composto e represente em um diagrama de corpo livre todas as forças, identificando-as, que atuam em cada um deles; use como referência a vista lateral do sistema.
- Escreva as equações do movimento de rotação do disco composto e de translação dos blocos.
- Determine a aceleração angular, , do disco composto.
- Determine matematicamente a condição para que o sistema esteja em equilíbrio
Questão 7
Uma roldana com de raio está montada num eixo horizontal sem atrito. O momento de inércia da roldana em relação ao eixo de rotação é . Uma corda de massa desprezível está enrolada na roldana e presa a um bloco de que desliza sobre uma superfície horizontal sem atrito. A corda não desliza em relação à roldana. Se uma força horizontal de módulo é aplicada ao bloco, qual é o módulo da aceleração angular da roldana?
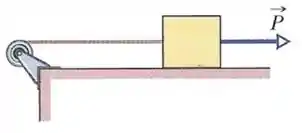
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 8
Uma roldana tem a forma de um disco uniforme de massa e raio (ver figura). A roldana está presa ao teto e gira livremente ao redor do seu centro. Um fio ideal passa pela roldana sem deslizar. Este fio está preso aos blocos e , de modo que os módulos das tensões indicadas valem, respectivamente, e
Dados: Considere e utilize que o momento de inércia de um disco uniforme de massa e raio em relação ao eixo que passa no seu centro de massa e é perpendicular à sua superfície é .
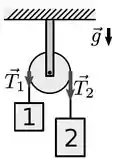
Calcule
- O módulo do torque devido à , em relação ao centro de massa da roldana
- O módulo da aceleração angular que a roldana está sujeita
Questão 9
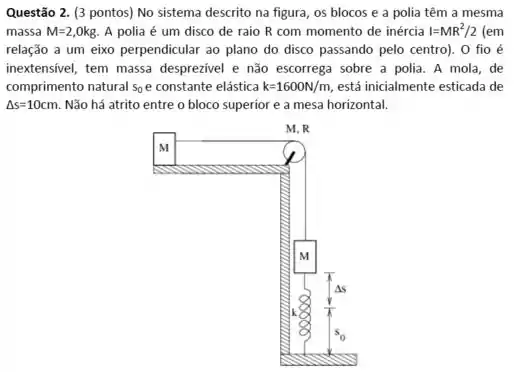
Um bloco de massa está preso a uma mola por uma corda inextensível e sem massa que passa por uma roldana de massa e raio , conforme mostrado na figura abaixo. A constante elástica da mola é . Trate a roldana como um disco maciço e homogêneo, despreze o atrito no eixo da roldana e assuma que o sistema parte do repouso com a mola não distendida.
Dado: Momento de inércia da roldana:
- A velocidade do bloco após ele cair
- A distensão máxima da mola.

Questão 10
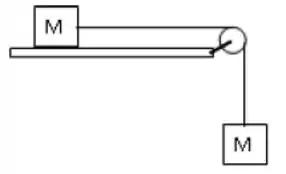
Dois blocos de massas e , como mostrado na figura, estão ligados por um fio e massa desprezível passando sobre uma polia de raio e massa . A polia é um disco uniforme e a corda não desliza sobre a polia. Desconsidere atrito no plano inclinado.
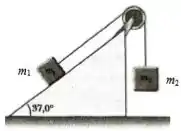
- Desenhe o diagrama de corpo livre para cada bloco e a polia.
- Determine a aceleração de cada bloco.
- Determine as tensões no cabo.
Questão 11
Na figura, um fio sem massa e inextensível passa sem escorregar ao redor da polia. Numa extremidade do fio é pendurado um bloco de massa m2 = 500 g, na outra, um bloco de massa m1 = 400 g, e a polia, que é um disco homogêneo montado num eixo horizontal sem atrito, tem um raio de 5,00 cm. Quando o sistema é abandonado a partir do repouso, o bloco de massa maior cai 75,0 cm e adquire uma velocidade linear de 30,0 cm/s.
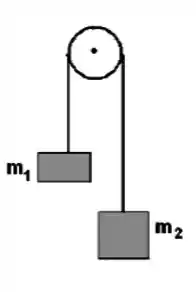
a) Faça os diagramas de força para cada bloco e polia.
b) Utilizando a conservação de energia mecânica determine a inércia rotacional da polia.
c) Determine o módulo e sentido da aceleração angular da polia.
d) Determine as tensões no fio e o vetor reação do eixo de rotação sobre a polia.
e) Qual é o vetor torque resultante em torno do eixo de rotação ? Faça dois cálculos, um utilizando a equação e outro .
f) Qual a força de atrito entre a corda e a polia?
Ver solução completaQuestão 12
Os blocos de massas e estão conectados por uma corda sem massa que passa por uma polia, como mostrado na figura. A polia é um disco homogêneo que pode girar em torno do seu eixo sem atrito. A massa desliza sem atrito sobre uma superfície horizontal. Os dois blocos estão em repouso quando a massa é liberada.
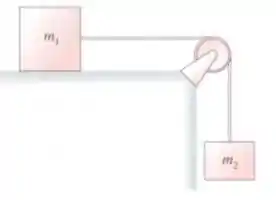
a) suponha que a massa da polia seja desprezível. Encontre as acelerações dos blocos e e a tensão na corda.
b) Suponha agora que a massa da polia é e seu raio é R. Encontre a aceleração de e as tensões nas partes vertical e horizontal da corda. Verifique que seus resultados condizem com os obtidos no item a) quando você faz =0
Ver solução completaQuestão 13
Um corpo de massa está suspenso por um fio de massa desprezível enrolado numa polia de raio . A polia consiste em um disco rígido do qual foi retirado um pedaço, como mostra a figura. A polia tem massa e gira sem atrito em torno de um eixo que passa pelo seu centro. Se a massa desce com aceleração de módulo , o momento de inércia da polia é:
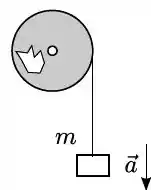
- ;
- ;
- ;
- ;
- ;
Questão 14
Uma máquina de Atwood possui massas , e uma polia maciça uniforme de massa M =2,0kg. O módulo da aceleração linear da massa vale:
a)
b)
c)
d)
e)
Questão 15
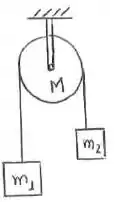
Um fio inextensível de massa desprezível é enrolado diversas vezes em torno da periferia de um cilindro maciço de raio , segue horizontalmente até a periferia de outro cilindro de raio , pela qual passa e segue verticalmente, até sua extremidade, na qual está suspenso um bloco de massa . Os cilindros, cada um também de massa , são homogêneos e podem girar sem atrito, cada um em torno de seu eixo fixo. O bloco desce verticalmente puxando o fio que fica tenso e faz os cilindros girarem, sem deslizar sobre suas periferias. (O momento de inércia de um cilindro homogêneo de massa e raio relativo ao seu eixo é )
- Faça um diagrama das forças externas que agem sobre o cilindro de raio
- Calcule o módulo da aceleração com que desce o bloco.
- Obtenha o módulo da aceleração angular de cada cilindro.
- Calcule o módulo da tensão no trecho vertical do fio e o módulo da tensão no trecho horizontal do fio.
Questão 16
(Capítulo 9.1 – Exercício 72) No sistema do problema 71, o bloco de é largado do repouso. (a) Determine a rapidez do bloco depois de ele ter caído uma distância de . (b) Qual é a rapidez angular da polia neste instante?
Ver solução completaQuestão 17
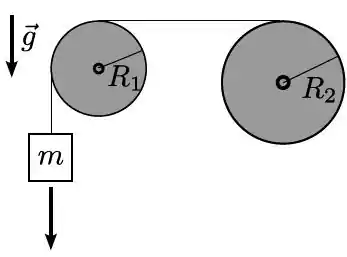
Um engenheiro monta um sistema que se constitui de dois cilindros de raios e unidos de forma que o centro da face circular do primeiro cilindro coincida com o centro da face circular do segundo. Em cada um dos cilindros com diferentes raios é enrolado um fio ideal. Este sistema pode girar sem atrito em torno de um eixo colocado no centro da face circular dos cilindros. O sistema pode ser observado nas figuras abaixo com visão lateral e frontal. A massa do cilindro menor de raio vale e a massa do cilindro de maior raio vale . O raio é igual ao dobro de . Para a aceleração da gravidade adote .
O momento de inércia de um disco girando em torno do seu centro de massa vale .
a) Escreva o momento de inércia deste sistema envolvendo os dois cilindros girando em torno do eixo apresentado na figura em termos de suas massas e dos seus raios.
b) Duas massas e são colocadas nos fios enrolados em cada um dos cilindros conforme a figura do enunciado. Faço o diagrama de corpo livre representando as forças que atuam na massa A, na massa B e no cilindro.
c) Em termos dos dados apresentados, escreva qual deve ser a relação entre as massas e para o sistema ficar em repouso em função das variáveis do problema dadas no enunciado.
d) Suponha que seja igual a e lembrando que . Nesta condição o sistema entrará em movimento. Calcule a aceleração angular dos cilindros em termos das variáveis dadas no enunciado.
e) Na condição dada no item (d), com e , sabe-se que o sistema se encontra inicialmente em repouso. Após o sistema ser liberado ele entra em movimento. Determine a velocidade angular dos cilindros após a massa A se deslocar de uma altura (a massa B irá se deslocar de ) em termos das variáveis dadas no enunciado utilizando a conservação de energia mecânica.
Ver solução completaQuestão 18
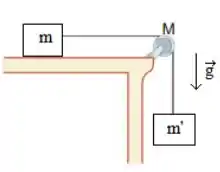
Considere o sistema mostrado na figura abaixo. A massa , que desliza sem atrito, está ligada à massa suspensa pelo fio que passa sem deslizar sobre uma polia homongênea de massa e raio . A polia gira sem atrito sobre um eixo horizontal, perpendicular ao plano da polia, que passa por seu centro de massa. A aceleração da gravidade é dada por e o momento de inércia da polia em relação ao eixo mencionado vale . A aceleração da massa , em termos de , , e é:
Questão 19
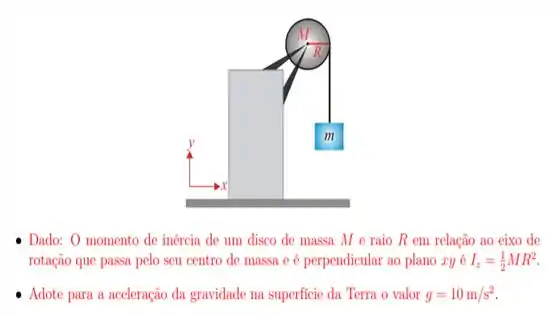
16. Uma polia homogênea, que possui o formato de um disco com raio e massa , está fixa em um suporte podendo girar livremente, sem atrito, em volta de um eixo que passa pelo seu centro e é perpendicular ao plano . Uma corda leve (de massa desprezível), que está enrolada nessa polia, prende um bloco de massa como mostra a figura. À medida que a polia gira, o bloco se movimenta para baixo, sem que a corda escorregue sobre a polia. O módulo do vetor aceleração de queda do bloco, em , vale aproximadamente:
Questão 20
(Capítulo 9.1 – Exercício 76) O sistema da figura 9-57 é largado do repouso quando o bloco de está acima da prateleira. A polia é um disco uniforme de com um raio de . Justo antes de o bloco de atingir a prateleira, determine (a) sua rapidez, (b) a rapidez angular da polia e (c) a tensão nos fios. (d) Determine o tempo de queda do bloco de . Suponha que o fio não deslize na polia.
Ver solução completaQuestão 21
Um bloco de massa encontra-se suspenso por uma corda ideal que passa por uma roldana de raio , com momento de inércia . A corda encontra-se enrolada ao cilindro central de um carretel na outra extremidade. O bloco é liberado a partir do repouso. A roldana e o carretel podem girar livremente (sem atrito) em torno de seus eixos fixos. Os centros de massa dos carretéis estão em repouso, não transladam.
- Considere os três carretéis abaixo feitos de materiais diferentes, com formas diferentes, de modo a terem a mesma massa. As distribuições de massa são homogêneas nas partes sólidas. Os três carretéis possuem o mesmo cilindro central. Com qual dos carretéis o bloco teria o menor valor da aceleração? Justifique sua resposta.
- Calcule o momento de inércia do carretel , considerando que cada uma das hastes é delgada, tem massa 𝑀 e comprimento . Os anéis são finos com massa 𝑀 e raio 𝑅. O cilindro central possui massa e raio .
- Sabendo-se que o carretel utilizado foi o . Qual a aceleração adquirida pelo bloco durante sua queda? Admita , , , , e .
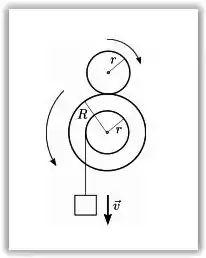
Questão 22
Duas polias dentadas estão conectadas sem que ocorra deslizamento entre elas. A polia menor possui raio r e a maior, raio R. A polia maior está conectada a um objeto através de um fio ideal e uma engrenagem interna de raio r, conforme a figura. Em um dado instante, o objeto desce verticalmente com velocidade v. Nesse instante, a velocidade angular da polia menor é dada por:
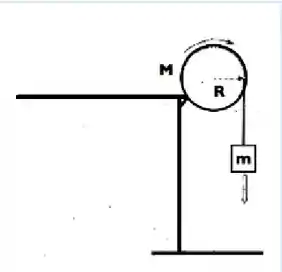
Questão 23
Um bloco de massa , suspenso por uma polia de raio e massa , é solto a partir do repouso. Considere a polia como um disco de densidade uniforme. Qual é a aceleração do bloco?
a)
b)
c)
d)
e)
Ver solução completaQuestão 24
Dois blocos de massas e , com estão ligados por uma corda de massa desprezível que passa, sem deslizar, por uma polia de massa e raio , como mostrado na figura. A polia gira sem atrito sobre um eixo que atravessa seu centro de massa. Julgue as afirmações abaixo:
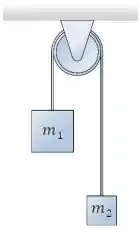
() O módulo da tração exercida pela corda sobre o bloco 1 é igual ao módulo da tração exercida pela corda no bloco 2.
() O módulo da tração exercida pela corda sobre o bloco 1 é maior que o módulo da tração exercida pela corda sobre o bloco 2.
() A aceleração angular da polia é diretamente proporcional à diferença entre as trações exercidas pela corda nos blocos 1 e 2.
Qual opção abaixo contém todas as afirmações que estão corretas?
(A)
(B)
(C) e
(D) e
(E) e
Ver solução completaQuestão 25
Um elevador pode ser representado esquematicamente como um bloco de massa para indicar a cabine (caixa de metal + carga), um bloco de massa representa um contra-peso para a cabine e uma polia de raio cujo momento de inércia é . Um motor está acoplado a polia e pode realizar um torque para tracionar os cabos (considerados ideais). O módulo da tração sobre a massa é , enquanto é a tração sobre . Considere que os cabos não deslizam sobre a polia e utilize .
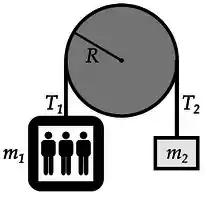
(a) Represente diagramaticamente todas as forças que atuam sobre as massas e e os torques sobre a polia.
(b) Escreva a segunda lei de Newton as massas , e a polia em termos da aceleração a da massa .
(c) Considere que a polia move-se com velocidade angular constante, de módulo . Qual é o módulo da potência que deve ser aplicada ao motor?
Ver solução completaQuestão 26
Dois blocos de massas e estão conectados por um fio ideal, como mostrado na figura. Se o raio da polia é de e seu momento de inércia em relação ao eixo de rotação é igual a , qual é o módulo da aceleração de cada um dos blocos (em função da aceleração da gravidade )?
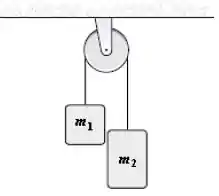
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 27
Um bloco de inércia e um bloco de inércia são conectados por uma corda com inércia desprezível sobre uma polia em forma de um disco sólido com raio e inércia . A rampa faz um ângulo de . O coeficiente de atrito cinético é para ambos os blocos. Use .
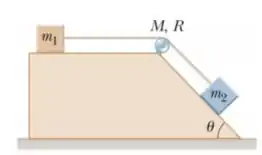
a) Desenha diagramas de corpo livre para o bloco 2 e o diagrama de corpo livre estendido para a polia.
b) Determine a aceleração dos dois blocos.
c) Calcule as tensões na corda, presa no bloco 1 e presa no bloco 2.
d) Qual a aceleração angular da polia?
Ver solução completaQuestão 28
Uma corda ideal está enrolada na periferia de uma casca esférica (massa e raio ) que gira em torno de um eixo vertical. A corda conecta a casca a uma roldana ( e ) e finalmente a um bloco pendurado de massa . A corda não desliza sobre a casca nem sobre a roldana e a casca e a roldana giram sem atrito em torno de seus eixos. Considere , e .
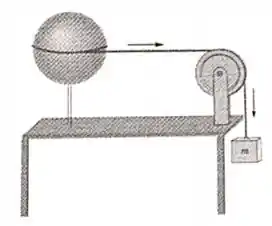
Com o sistema partindo do repouso, o bloco desce com aceleração e a roldana sofre deslocamento angular até que o bloco esteja na iminência de tocar o solo.
a) Calcule o tempo de queda do bloco e a velocidade angular final da casca.
b) Para o bloco, represente num diagrama de forças as forças relevantes para seu movimento de translação e escreva a Segunda Lei de Newton associada.
c) Para a casca, represente num diagrama de forças as forças relevantes para seu movimento de translação e escreva a Segunda Lei de Newton associada.
d) Para a roldana, represente num diagrama de forças as forças relevantes para seu movimento de translação e escreva a Segunda Lei de Newton associada.
e) Determine o valor da massa do bloco.
Ver solução completaQuestão 30
Dois cilindros de raios diferentes são unidos conforme a figura, sendo o raio do cilindro menor e do cilindro maior . Fios ideais, que não escorregam, são enrolados em cada um dos cilindros e na outra extremidade de cada um dos fio é pendurada uma massa . Este sistema é colocado para girar ao redor de um eixo de rotação horizontal, sem atrito. O momento de inércia deste sistema torno do eixo vale . O sistema inicialmente se encontra em repouso. Após deixarmos os pesos cair, determine a aceleração angular deste sistema utilizando as leis de Newton em termos de , a aceleração da gravidade, e de . NÃO substitua por valores numéricos.
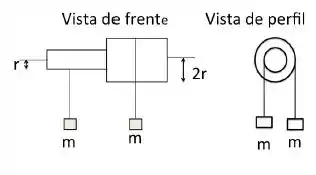
Questão 31
Um fio inextensível e de massa desprezível é enrolado em torno de uma polia de raio 0,40m. Um bloco amarrado na ponta deste fio é liberado do repouso, descendo 1,5 m em 2,0 segundos e fazendo a polia girar sem deslizamento do fio. Se a tensão na corda durante a descida do bloco vale 20 N, o momento de inércia da polia vale:
(A)
(B) 3.7 kg ·
(C) 3.9 kg ·
(D) 4.1 kg ·
(E) 4.3 kg ·
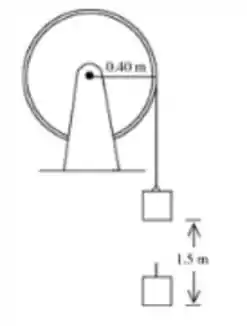
Questão 32
(Capítulo 9.1 – Exercício 75) Um carro de está sendo retirado da água por um guincho. No momento em que o carro está acima da água, a caixa de engrenagens quebra e o tambor do guincho gira livremente enquanto o carro cai. Durante a queda do carro, não existe deslizamento entre a corda (sem massa), a polia e o tambor. O momento de inércia do tambor do guincho é e o momento de inércia da polia é . O raio do tambor é e o raio da polia é . Suponha o carro partindo do repouso. Determine a rapidez com que ele atinge a água.
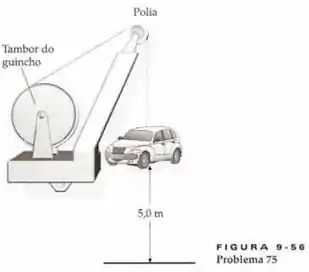
Questão 33
Dois blocos de massa e são conectados por uma corda inextensível sem massa por uma polia de massa e momento angular e raio , que gira em torno do seu eixo de simetria, em um plano inclinado com atrito dinâmico . O conjunto se move com se movendo para baixo e se movendo para cima. Considerando que a segunda lei de Newton fornece as equações do movimento de um corpo:
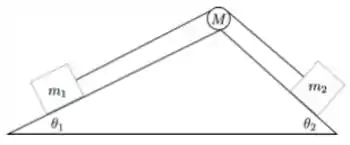
a) (1 ponto) Escreva a equação de movimento para os blocos de massa e ;
b) (1 ponto) Escreva a equação de movimento para a polia de massa ;
c) (1 ponto) A partir dos seus resultados nos itens anteriores, calcule a aceleração linear do sistema e as trações no fio;
Ver solução completaQuestão 34
(Capítulo 9.1 – Exercício 71) O sistema mostrado na figura consiste em um bloco de colocado sobre uma prateleira horizontal sem atrito. Este bloco está preso a um cordão que passa por uma polia e tem sua outra extremida presa a um bloco pendente . A polia é um disco uniforme de de raio e de massa. Determine a aceleração de cada bloco e as tensões no cordão.

Questão 35
Em uma exposição para vendas, um carro de massa é mantido a uma certa altura do solo através de um cabo ligado a um guindaste. Em um dado instante a trava que mantém o carro elevado falha e ao mesmo tempo começa a cair, fazendo o cabo desenrolar do tambor (cilindro maciço de raio e massa ) e girar a polia superior de raio e massa .
Após cair por uma distância o sistema de segurança da máquina é acionado, fazendo com que o carro pare. Durante a queda, pode-se desprezar deslizamentos no movimento do cabo pelo tambor e pela polia.
Responda as perguntas abaixo desprezando a massa do cabo e apresente as respostas em função de , , , , , e .
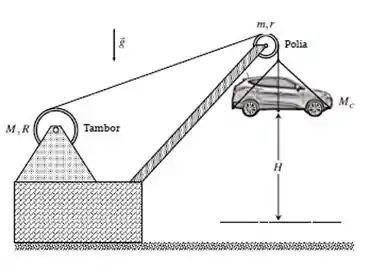
(a) Calcule o módulo da velocidade do carro no instante imediatamente anterior ao acionamento do sistema de segurança.
(b) Calcule o módulo da aceleração do carro durante sua queda
(c) Calcule o módulo da tensão no cabo no trecho entre o tambor e a polia durante a queda do carro
Ver solução completaQuestão 36
Um bloco de massa está pendurado por um fio ideal que está enrolado em uma polia fixa, mas que pode girar em torno de um eixo que passa pelo seu centro e é perpendicular ao plano da polia. À medida que o bloco desce, o fio vai se desenrolando e a polia vai adquirindo uma velocidade de rotação cada vez maior, como sugere a figura abaixo. Suponha que o fio não deslize sobre a periferia da polia. A polia tem raio e observa-se que o bloco desce com aceleração constante de módulo . As respostas devem ser dadas em termos dos dados do problema: , , e da aceleração da gravidade .
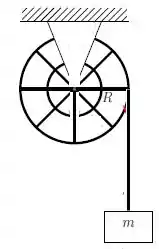
a) Supondo que o sistema parte do repouso, quanto tempo leva para que a polia dê a primeira volta completa em torno do eixo de rotação.
b) Faça um diagrama das forças que atuam sobre o bloco e sobre a polia.
c) Qual o momento de inércia da polia em relação ao seu eixo de rotação?
Ver solução completaQuestão 37
Um cabo ideal está enrolado em volta de uma polia de raio e massa e tem sua outra extremidade ligada a um bloco de . O bloco se encontra apoiado sobre um plano inclinado de em relação a horizontal. O sistema é solto a partir do repouso. Não existe atrito entre o plano e o bloco. Considerando o momento de inércia da polia calcule:
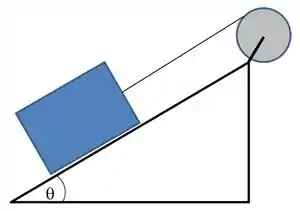
A aceleração angular da polia.
a tração no cabo e o torque na polia.
O módulo da aceleração linear de um ponto na borda na polia após de iniciado o movimento.
Ver solução completaQuestão 38
(Capítulo 9.1 – Exercício 74) No sistema mostrado na figura, o bloco de está sobre a prateleira horizontal. O coeficiente de atrito cinético entre a prateleira e o bloco é . O bloco está preso a um cordão que passa pela polia e tem sua outra extremidade presa a um bloco pendente de . A polia é um disco uniforme de de raio e de massa. Determine a aceleração de cada bloco e as tensões no cordão.

Questão 39
(Cap 10 – Ex 69) Na Fig. 10-49, dois blocos de estão ligados por uma corda de massa desprezível que passa por uma polia de de raio e momento de inércia . A corda não escorrega na polia; não se sabe se existe atrito entre a mesa e o bloco que escorrega; não há atrito no eixo da polia. Quando o sistema é liberado a partir do repouso, a polia gira de em e a aceleração dos blocos é constante. Determine
a) o módulo da aceleração angular da polia,
b) o módulo da aceleração de cada bloco,
c) a tensão , da corda e
d) a tensão da corda.
Ver solução completaQuestão 40
. Os cilindros mostrados na Figura têm raios e , massas e e momentos de inércia em relação a seus centros de massa determinados pela relação geral . Os cilindros são livres para girar em torno de eixos horizontais fixos, perpendiculares à figura e que passam pelos respectivos centros de massa. O fio de massa desprezível passa sem deslizamento pelos cilindros e suas pontas livres estão presas a corpos de massas e , em repouso na mesma altura. Determine a aceleração dos corpos e a velocidade do corpo quando este se deslocou . Adote .
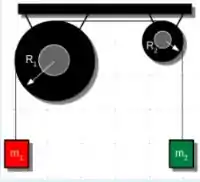
Questão 41
2) A figura a seguir ilustra um dispositivo conhecido como máquina de Atwood, onde dois corpos estão conectados por meio de um fio que passa por uma polia fixa. Considere que as massas dos corpos e valem, respectivamente, e , que a polia pode girar sem atrito em torno do seu eixo e que o fio leve e inextensível não desliza sobre a polia de massa e raio , cujo momento de inércia em relação ao seu eixo de rotação é
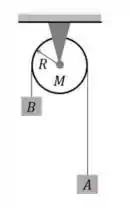
Quando os blocos e são liberados a partir do repouso, em um local onde a aceleração gravitacional
é igual a , a polia adquire uma aceleração angular de módulo igual a:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 42
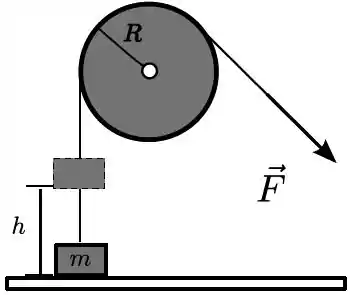
Um disco de raio e massa encontra-se fixado a uma parede vertical em um pino que passa pelo seu centro. Um cabo de massa desprezível passando pela sua periferia tem na sua extremidade um bloco de massa sobre uma superfície horizontal. O cabo é puxado por uma força constante , ergendo o bloco de uma altura , como mostra a figura. Desprezando-se o efeito de atrito entre o pino e o disco e considerando que o bloco e o disco estavam em repouso no momento em que a força começou a agira calcule:
- A aceleração com que o bloco é erguido;
- O módulo da tração que age sobre o trecho do cabo entre o disco e o bloco;
- A energia cinética adquirida pelo disco imediatamente após o bloco ser erguido da altura .
Dado: o momento de inércia do disco para um eixo que passa perpendicularmente ao disco e pelo seu centro é .
Questão 43
Uma roldana de massa e raio está montada num eixo horizontal sem atrito. O momento de inércia da roldana em relação ao eixo de rotação é . Uma corda de massa desprezível está enrolada na roldana. Na extremidade livre da corda está suspenso um bloco de massa . A corda não desliza em relação à roldana. O sistema é liberado a partir do repouso. Enquanto o bloco desce qual é a tensão na corda?
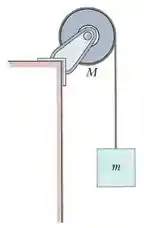
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 44
Duas massas e estão penduradas por fios inextensíveis e de massas desprezíveis a uma polia. A polia é formada por discos, ligados de maneira que formam um corpo único. Considere o momento de inércia total da polia em relação ao seu centro de massa como sendo . O fio ligado a está enrolado no disco externo de raio e o fio ligado a está enrolado no disco interno de raio . Despreze o atrito.
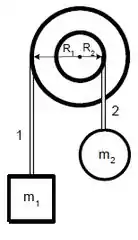
- Escreva as equações de movimento (2ª Lei de Newton) para o sistema de forma que fosse possível determinar a aceleração angular da polia .
- Suponha agora que e . Se , e , o sistema se encontra em equilíbrio estático. Calcule os torques e que os fios realizam sobre o corpo.
- Suponha que uma massa de seja adicionada no topo da massa dada no item anterior e que o sistema entre em movimento. No instante de tempo em que a massa tiver alcançado em módulo uma velocidade , calcule o módulo da velocidade da massa neste mesmo instante.
Escreva os torques primeiro em notação literal para então substituir os valores dados. Utilize o sistema de coordenadas indicado.
Questão 47
O objeto ilustrado ao lado é composto por um cilindro de raio , uma haste rígida e dois discos afastados do eixo de rotação. O objeto tem momento de inércia . Ao longo do perímetro do cilindro está enrolada uma corda inextensível de massa desprezível. Outra parte desta corda está enrolada em uma roldana de raio e momento de inércia . Na extremidade da corda está uma pequeno cubo de massa , distante de um suporte. Não há deslizamento na corda. Inicialmente o sistema é mantido em repouso através de um freio. No instante o freio é retirado e o sistema inicia seu movimento. Utilize para a aceleração da gravidade.
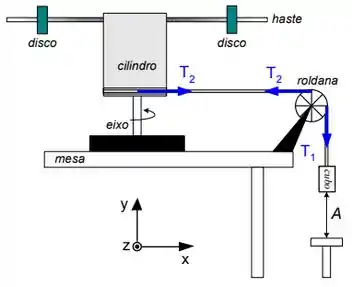
b) Determine a razão entre os módulos das acelerações angulares da roldana e do objeto .
c) Determine o módulo da aceleração linear com que o cubo cai em função dos parâmetros dados.
Ver solução completa