Na Fig. 13-33, três esferas de 5,00 kg estão localizadas a distâncias de e . Qual é (a) o módulo e (b) a orientação (em relação ao semieixo x positivo) da força gravitacional a que está sujeita a esfera B?
Passo 1
Bom, como as massas A e C puxam B, a direção da resultante vai ficar inclinada com relação ao semieixo x.
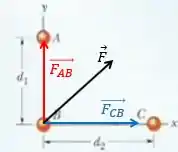
é a força que exerce em B.
é a força que exerce em B.
é a força que resultante em B.
Neste problema a gente vai usar a equação da força gravitacional pra calcular as componentes da força resultante e, depois, calculamos o módulo dela e a sua direção. Nada que uma trigonometria boa não resolva ;)
Passo 2
Vamos calcular primeiro as componentes do vetor força resultante, que são a atração gravitacional exercida por C no eixo x e por A no eixo y.
Passo 3
Agora que já temos as componentes, podemos usar trigonometria em um triângulo retângulo, para achar o módulo e o ângulo dela com o semieixo x.
E o , vamos usar tangente:
Resposta
(a)
(b)