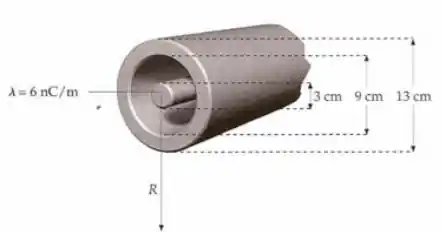
A Figura 22-42 mostra uma porção da seção transversal de um cubo concêntrico infinitamente longo. O condutor interno tem uma densidade linear de carga de e o condutor externo não tem carga resultante. (a) Determine o campo elétrico para todos os valores de , onde é a distância perpendicular ao eixo comum do sistema cilíndrico. (b) Quais são as densidades superficiais de carga nas superfícies do lado de dentro e do lado de fora do condutor externo?
Passo 1
Eai galera. Temos mais um problema de simetria cilíndrica! Aqui também devemos usar o conceito de indução total. Sejam: o raio do cilindro interno; o raio da parte interna do cilindro externo e o raio da parte externa do cilindro externo.
Passo 2
- Para , temos pois ele estará no interior de um condutor em equilíbrio eletrostático. Assim, não pode haver campo elétrico.
- Para , poderemos usar a lei de Gauss. Veja a figura abaixo
- Para , segue que o campo elétrico é nulo, pois estamos no interior de um condutor em equilíbrio eletrostático.
- Para toda a carga resultante na lei de Gauss será a carga do cilindro interna, pois o cilindro externo não está carregado. Logo, o campo terá exatamente a mesma forma do calculado para :
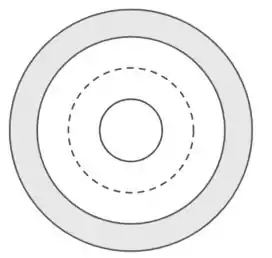
Na figura acima o círculo tracejado representa o cilindro gaussiano. Dessa forma, temos que
Logo,
Passo 3
Para a parte externa, temos
Resposta
Ei, a resposta está no passo a passo :)