Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.4 - Ex. 48
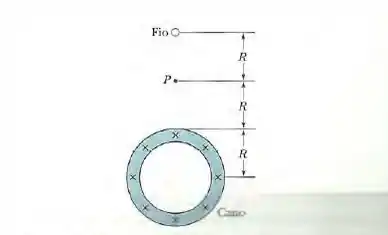
Na figura 29-71, um cano circular longo de raio externo conduz uma corrente (uniformemente distribuída) para dentro do papel. Existe um fio paralelo ao cano a uma distância de do eixo do cano. Determine (a) o valor e (b) o sentido (para dentro ou para fora do papel) da corrente no fio para que o campo magnético no ponto tenha o mesmo módulo que o campo magnético no eixo do cano e o sentido oposto.
Passo 1
Fala aí! tudo certinho? 😇
Nesse problema temos um cano circular longo de raio externo conduz uma corrente (uniformemente distribuída) para dentro do papel. Existe um fio paralelo ao cano a uma distância de do eixo do cano e nosso objetivo é determine o valor e o sentido (para dentro ou para fora do papel) da corrente no fio para que o campo magnético no ponto tenha o mesmo módulo que o campo magnético no eixo do cano e o sentido oposto.
Tem ideia de como fazer isso? 🤔
A lei de Àmpere é utilizada para determinar o campo magnético total de uma região que apresente algum tipo de simetria. De acordo com ela:
O círculo do sinal de integral indica que a integração do produto escalar deve ser realizada para uma curva fecahda, conhecida como amperiana.
A corrente é a corrente total envolvida pela curva fechada. Essa corrente tamém pode ser escrita como:
onde é a densidade de corrente na curva fechada.
Bora começar! 😉
Passo 2
Por simetria, o cmapo magnético no eixo do cano se deve apenas ao fio, e o módulo desse campo é:
Como o campo produzido pelo fio no ponto é maior que o campo produzido pelo fio no eixo do cano, para que o campo total no ponto seja igual ao campo no eixo do cano é preciso que o campo produzido pelo cano no ponto tenha o sentido oposto ao do campo produzido pelo fio. Assim:
Fazendo , obtemos
O sentido da corrente é para dentro do papel.
E aí! entendeu tudo? Responde Aí! 😎
Resposta
a) ;
b) O sentido da corrente é para dentro do papel.