Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são = 10,0 μF, = 5,00 μF e = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica e passa a se comportar como um condutor, determine
(a) o aumento da carga do capacitor 1;
(b) o aumento da diferença de potencial entre as placas do capacitor 1.
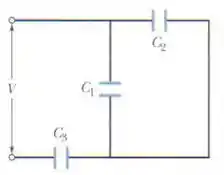
Passo 1
Vamos calcular a capacitância equivalente antes da ruptura:
e estão em paralelo e eles estão em série com , então fica assim:
Passo 2
Agora podemos nos livrar de . O circuito fica assim:
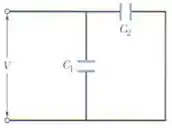
Vamos calcular o potencial de . A ideia é conservar a carga do sistema inteiro. Antes a carga era
e depois passou a ser
é a capacitância equivalente depois, ou seja, . Agora é só igualar, já que carga do sistema se conserva (veja bem, do sistema, não em cada capacitor)
Passo 3
Substitua os valores:
Vamos responder a (b) primeiro. A voltagem em 1 era de 100,0 V, e agora é 21,1 V. Então:
Passo 4
Agora vamos para a letra (a):
Agora é substituir os valores:
Resposta
Letra (a):
Letra (b):