Exercícios de Capacitância Equivalente - Lista de Exercícios Resolvida
Questão 1
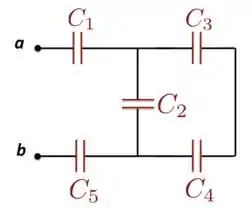
Dado o circuito abaixo:
- Calcule a capacitância de em função da capacitância ;
- Calcule a capacitância equivalente do circuito todo em função da capacitância ;
Questão 2
Um capacitor é formado por duas placas condutoras planas e paralelas de área cada uma, separadas por uma distância muito menor que as suas dimensões. Um material isolante de constante dielétrica é inserido no capacitor de forma a ocupar metade do volume entre as placas, como mostrado na figura abaixo, ficando completamente em contato com uma delas, enquanto a outra metade permanece no vácuo. A seguir, uma diferença de potencial é aplicada entre as placas. Em termos de e , determine para esse sistema:
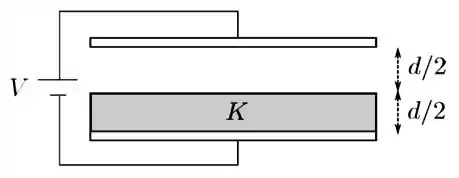
- A capacitância do sistema.
- Os módulos do campo elétrico na metade vazia () e na metade com dielétrico ().
Questão 3
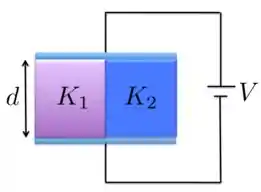
Um capacitor com placas paralelas possui o espaço entre as placas preenchido com duas camadas de dielétricos, uma com constante dielétrica e a outra com a constante dielétrica , como mostra a Figura abaixo. Cada camada possui espessura igual à distância entre as placas e cada camada preenche o espaço entre as placas. Se as placas são mantidas à uma diferença de potencial fixa , então mostre que capacitância é dada por
Questão 4
Na Figura abaixo, e . A diferença de potencial aplicada é .
- Qual é a capacitância equivalente do circuito entre os pontos e ?
- Calcule a carga de cada capacitor e a diferença de potencial através de cada capacitor.
Questão 5
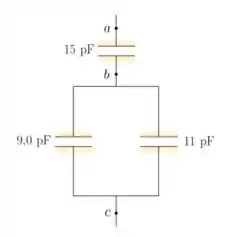
Para o sistema de capacitores mostrado na figura abaixo, encontre a capacitância equivalente
(a) entre e ; e
(b) entre e .
Questão 6
Três placas condutoras de área são espaçadas de por vácuo (região ) e de por um material de constante dielétrica (região ), como indicado na figura. A carga total na placa superior é igual a , na placa do meio é igual a zero e na placa inferior é igual a . Desconsidere a não uniformidade do campo elétrico perto das bordas.
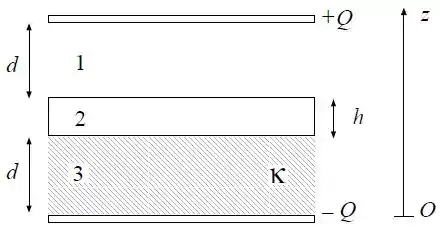
Indique numa figura e calcule as densidades de carga nas superfícies das placas condutoras. Calcule o vetor campo elétrico nas regiões e . Expresse suas respostas em termos de e.
Calcule a capacitância do sistema de três placas.
Calcule a densidade de carga de polarização no dielétrico.
Ver solução completaQuestão 7
Um capacitor de placas planas e paralelas, de área , a distância , é “recheado” por uma chapa condutora, também de área , e espessura .

A capacitância de tal capacitor é:
Questão 8
A figura mostra um capacitor de placas paralelas com uma área das placas e uma distância entre as placas .
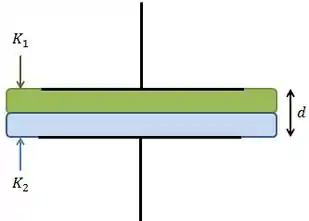
A metade superior do espaço entre as placas é preenchida por um material de constante dielétrica .
A metade inferior é preenchida por um material de constante dielétrica .
Qual é a capacitância?
Ver solução completaQuestão 9
Um capacitor de capacitância é conectado inicialmente a uma bateria e carregado até armazenar uma carga . A seguir, o capacitor é desconectado da bateria e conectado a dois outros capacitores, inicialmente descarregados, de capacitâncias e , como mostrado na figura abaixo. Nessa nova configuração, após restabelecido o equilíbrio eletrostático, o capacitor armazena uma carga . Nessa situação, as cargas armazenadas nos capacitores e valem, respectivamente:
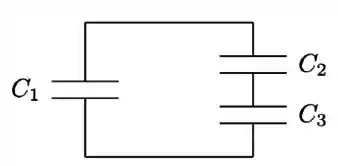
- e
- e
- e
- e
- e
- e
Questão 10
Dois capacitores, de capacitâncias e , são ligados em série a uma bateria que fornece uma voltagem ao sistema. A razão entre as cargas armazenadas nos capacitores e , e a razão entre as diferenças de potencial entre as placas dos dois capacitores são, respectivamente:
- e
- e
- e
- e
- e
Questão 11
Três placas condutoras de área são espaçadas de por vácuo (região ) e de por um material de constante dielétrica (região ), como indicado na figura. A carga total na placa superior é igual a , na placa do meio é igual a zero e na placa inferior é igual a . Desconsidere a não uniformidade do campo elétrico perto das bordas.
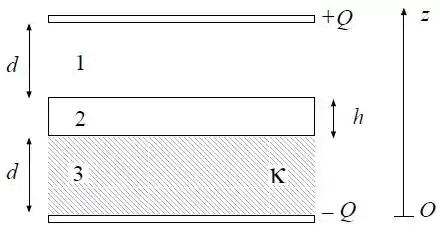
Indique numa figura e calcule as densidades de carga nas superfícies das placas condutoras. Calcule o vetor campo elétrico nas regiões e . Expresse suas respostas em termos de e.
Calcule a capacitância do sistema de três placas.
Calcule a densidade de carga de polarização no dielétrico.
Ver solução completaQuestão 12
Um capacitor de placas planas e paralelas de área , separadas por uma distância , possui uma capacitância quando há vácuo entre as placas. Por erro do fabricante, foi inserido no capacitor um material condutor, como mostrado na figura abaixo. Sabendo que a largura do material condutor vale e que os efeitos de borda podem ser desprezadas, a capacitância do sistema com o condutor dentro vale:
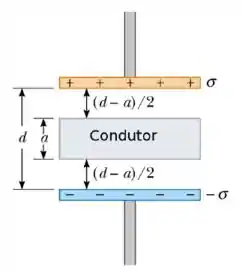
- 0
Questão 13
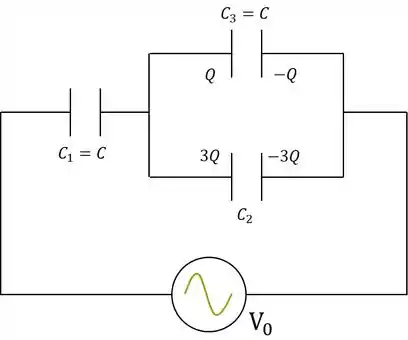
No circuito da figura abaixo uma bateria fornece uma diferença de potencial e os capacitores todos possuem a mesma capacitância .
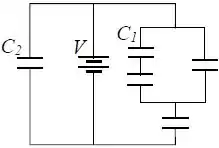
As cargas dos capacitores e são respectivamente:
; .
; .
; .
; .
; .
; .
Ver solução completaQuestão 14
Um capacitor é formado por duas placas condutoras planas e paralelas de área cada uma, separadas por uma distância muito menor que as suas dimensões. Um material isolante de constante dielétrica é inserido no capacitor de forma a ocupar metade do volume entre as placas, como mostrado na figura abaixo, ficando completamente em contato com uma delas, enquanto a outra metade permanece no vácuo. A seguir, uma diferença de potencial é aplicada entre as placas. Em termos de e , determine para esse sistema:
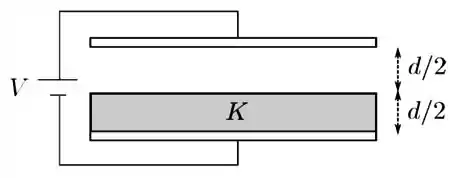
- A capacitância do sistema.
- Os módulos do campo elétrico na metade vazia () e na metade com dielétrico ().
Questão 15
(Cap 25 Ex- 28) A Fig. abaixo mostra uma bateria de e três capacitares descarregados de capacitâncias , e . A chave é deslocada para a esquerda até que o capacitar 1 esteja totalmente carregado. Em seguida, a chave é deslocada para a direita. Determine a carga final (a) do capacitar 1; (b) do capacitar 2; (c) do capacitar 3.
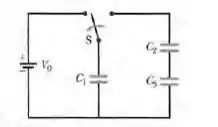
Questão 16
(Cap 25 Ex- 15) Na Fig. 25-31 , uma bateria de 20,0 V é ligada a um circuito constituído por capacitores de capacitâncias e . Determine (a) a capacitância equivalente do circuito; (b) a carga armazenada por ; (c) e (d) do capacitor 1; (e) e (f) do capacitor 2; (g) e (h) do capacitor 3.
Ver solução completaQuestão 17
a) Determine a capacitância associada a um capacitor de placas paralelas, quadradas, de lado , separadas por uma distância (onde ) para o caso em que o espaço entre as placas está ocupado pelo vácuo.
b) Suponha agora que o capacitor é preenchido com dois materiais diferentes cujas constantes dielétricas são e , respectivamente, na configuração mostrada na figura abaixo. Calcule a nova capacitância.
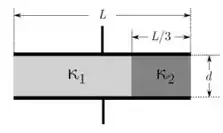
Questão 18
Usa-se uma bateria para carregar uma combinação de dois capacitores indênticos ligados em paralelo. Se a diferença de potencial nos terminais da bateria é e uma carga total flui pela bateria durante o processo de carga, então a carga em cada capacitor e a diferença de potencial através de cada um são:
a) e , respectivamente
b) e , respectivamente
c) e , respectivamente
d) e , respectivamente
e) e , respectivamente
Ver solução completaQuestão 19
Deseja-se conectar um capacitor de a outro de . Com qual tipo de ligação o capacitor de terá uma diferença de potencial maior através dele do que o capacitor de ? Com qual tipo de ligação o capacitor de terá um módulo de carga maior em cada placa do que o capacitor de ?
- Em série. Em série.
- Em paralelo. Em paralelo.
- Em série. Em paralelo.
- Em paralelo. Em série.
- Em série. Nem em série nem em paralelo.
Questão 20
Sobre capacitores e dielétricos, considere as afirmativas abaixo:
Numa associação em série de capacitores, a diferença de potencial em cada capacitor da associação é a mesma diferença de potencial atuando no capacitor equivalente.
Numa associação em paralelo de capacitores, a carga do capacitor equivalente é a soma das cargas em cada um dos capacitores da associação.
Um material dielétrico é inserido em um capacitor de placas planas e paralelas de forma a ocupar todo o volume entre as placas. Se o capacitor for mantido isolado durante a inserção, a energia potencial elétrica armazenada nele será maior do que antes da inserção.
São VERDADEIRAS as afirmativas:
e
e
e
, e
Nenhuma delas.
Ver solução completaQuestão 21
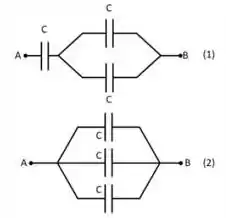
Considere os dois circuitos mostrados na figura abaixo. Todos os capacitores são idênticos e tem capacitâncias iguais a . A diferença de potencial entre os terminais e também é a mesma. Sejam e as capacitâncias equivalentes dos circuitos 1 e 2 entre os terminais e , respectivamente. Nessa situação, podemos afirmar que a razão vale:
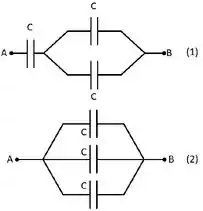
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 22
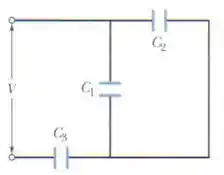
(Cap 25 Ex- 17) Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são = 10,0 μF, = 5,00 μF e = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica e passa a se comportar como um condutor, determine
(a) o aumento da carga do capacitor 1;
(b) o aumento da diferença de potencial entre as placas do capacitor 1.
Questão 23
(Cap 25 Ex- 14) Na Fig. 25-30, a bateria tem uma diferença de potencial V = 10,0 V e os cinco capacitores têm uma capacitância de 10,0 μF. Determine a carga (a) do capacitor 1; (b) do capacitor 2.
Ver solução completaQuestão 24
O capacitor é carregado separadamente por uma bateria até atingir uma carga de . Então ele é removido da bateria e ligado a dois outros capacitores e , como mostrado.
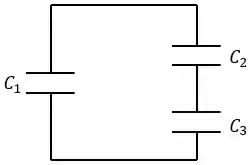
Agora a carga na placa positiva de é . As cargas nas placas positivas de e são:
e ;
e ;
e ;
e ;
e ;
Ver solução completaQuestão 25
(Cap 25 Ex- 9) Os três capacitores da Fig. 25-27 estão inicialmente descarregados e têm uma capacitância de 25,0 μF. Uma diferença de potencial V = 4200 V entre as placas dos capacitores é estabelecida quando a chave é fechada. Qual é a carga total que atravessa o medidor A?
Ver solução completaQuestão 26
Sobre capacitores, considere as afirmativas abaixo:
Numa associação em paralelo de capacitores, a diferença de potencial no capacitor equivalente é a soma das diferenças em cada um dos capacitores da associação.
Em uma associação em série de capacitores, a capacitância do capacitor equivalente é sempre menor que qualquer uma das capacitâncias de cada capacitor da associação.
A capacitância de um capacitor cilíndrico depende da carga elétrica contida no mesmo.
São VERDADEIRAS as afirmativas:
e
e
e
, e
Nenhuma delas.
Ver solução completaQuestão 27
(Cap 25 Ex- 13) Um capacitor de 100 pF é carregado com uma diferença de potencial de 50 V e a bateria usada para carregar o capacitor é desligada. Em seguida, o capacitor é ligado em paralelo com um segundo capacitor, inicialmente descarregado. Se a diferença de potencial entre as placas do primeiro capacitor cai para 35 V, qual é a capacitância do segundo capacitor?
Ver solução completaQuestão 28
Um capacitor esférico é formado por uma esfera interna de raio e uma camada esférica concêntrica de raio interno , conforme a figura.
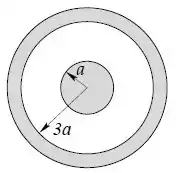
- Calcule a capacitância deste capacitor no vácuo a partir da definição.
- Como se altera a capacitância se o espaço entre os condutores for preenchido com um material de constante dielétrica ?
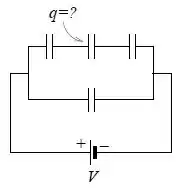
- Quatro capacitores de capacitância , inicialmente descarregados, foram associados e uma diferença de potencial foi aplicada, conforme a figura. Determine a carga na placa indicada na figura. Dê sua resposta em termos de e .
Questão 29
Um capacitor de placas planas e paralelas, de área , a distância , é “recheado” por uma chapa condutora, também de área , e espessura .

A capacitância de tal capacitor é:
Questão 30
Uma bateria de está conectada a dois capacitores, conforme a figura abaixo.
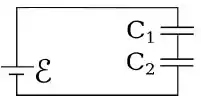
Nesta configuração, a capacitância e a carga do capacitor vale . Quanto vale a capacitância do capacitor ?
Ver solução completa
Questão 31
Um capacitor de e um de , quando carregado separadamente por uma bateria, adquirem cargas e , respectivamente. Quando são ligados em série e carregados pela mesma bateria, eles adquirem cargas e , respectivamente.
Então:
;
;
;
;
;
Ver solução completaQuestão 32
Um capacitor de placas paralelas e área , possui o espaço entre as placas preenchido por materiais dielétricos de diferentes constantes dielétricas ( e ), arranjados em diferentes espessuras ( e , respectivamente), como mostra a figura.
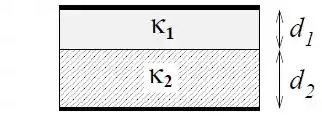
Calcule a capacitância de um capacitor de placas paralelas de área e distância entre placas, onde há vácuo, igual a . Dado: o campo elétrico entre as placas do capacitor é .
Calcule a capacitância do capacitor da figura.
A placa superior do capacitor está a um potencial 0 em relação à placa inferior. Determine a densidade de cargas livres na placa superior deste capacitor, e a densidade de cargas ligadas (ou induzidas) na face do dielétrico em contato com esta placa.
Ver solução completaQuestão 33
Considere os dois circuitos mostrados na figura abaixo. Todos os capacitores são idênticos e tem capacitâncias iguais a . A diferença de potencial entre os terminais e também é a mesma. Sejam e as capacitâncias equivalentes dos circuitos e entre os terminais e respectivamente. Nessa situação, podemos afirmar que a razão vale: