Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 6.Exercícios e Problemas - Ex. 15

A interação entre dois átomos idênticos para formar uma molécula diatômica pode ser descrita com boa aproximação pelo potencial de Lennard-Jones

Onde é a distância entre os núcleos dos dois átomos. Por simplicidade consideramos os dois átomos situados sobre o eixo dos . A) Determine a distância de equilíbrio , entre os dois átomos na molécula. B) Determine a energia de dissociação da molécula, isto é, a diferença de energia potencial entre as coordenadas e . C) Faça um gráfico do potencial, usando os dados referentes à molécula de . , .

Passo 1

Salve pessoas, tudo certo? Vamos lá! Primeiro, vamos entender como se dá essa distancia de equilíbrio! Significa que o potencial seja igual a . Aplicando pra equação:

Simplificando:

Podemos olhar assim: a única forma em que satisfaz a equação, é se:

E a única forma de potencias de razões serem iguais com potências diferentes, é se as razões forem , ou seja:

Logo,

Passo 2

Para achar essa é mais simples! Se a energia de dissociação da molécula é dada pela diferença de energia potencial usando: e , temos então que:

Quando um número é dividido por infinito, ou algo que se aproxima do infinito, o numero aproxima-se de 0, logo:

Aplicando agora o valor de , temos que:

Logo,

Fazendo a diferença,

Logo,

Passo 3

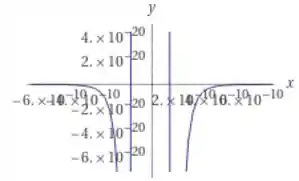
Para o gráfico, com os dados que a questão nos dá, temos:

Plotando o grafico,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você vence uma amiga, em uma corrida. No início, os dois têm a mesma energia cinética. mas ela está mais rápida do que você. Quando você eleva sua rapidez em 25 por cento, vocês passam a ter a mesma r

Uma partícula de 3,0 kg, que se move ao longo do eixo x, tem uma velocidade de +2,0 m/s quando passa pela origem. Ela está sujeita a uma força única, F x , que varia com a posição como mostrada na fig

Uma partícula de massa m move-se em uma dimensão com energia potencial U(x) representada pela curva da Fig.( as beiradas abruptas são idealizações de um potencial rapidamente variável. Inicialmente a

Uma partícula move-se ao longo da direção x sob o efeito de uma força F x =- k x + K x 2 , onde k = 200N / me K = 300N / m 2 . a) Calcule a energia potencial U(x) da partícula, tomando U(0) = 0, e faç

Um oscilador harmônico tridimensional isotrópico é definido como uma partícula que se move sob a ação de forças associadas à energia potencial U x , y , z = 1 2 k ( x 2 + y 2 + z 2 ) Onde k é uma cons