Exercícios de Força, Energia Potencial e Deslocamento - Lista de Exercícios Resolvida
Questão 1
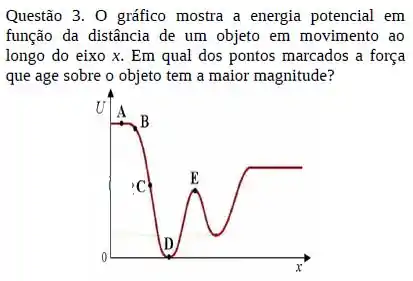
Uma única força conservativa atua em uma partícula paralela ao eixo horizontal de um sistema de coordenadas. A energia potencial desta força é dada pela figura abaixo. Qual opção representa corretamente os vetores (direção, intensidade e sentido) das forças que atuam sobre a partícula nos pontos e respectivamente.
![]()
- diagrama 4
- diagrama 1
- diagrama 5
- diagrama 2
- diagrama 3
Questão 2
A força sobre um corpo é dada por . Em , sabe-se que a força aponta no sentido e tem a magnitude de . Determine a energia potencial associada a esta força como função de , atribuindo um valor de referência de em para a energia potencial.
Ver solução completaQuestão 3
A energia potencial de um corpo restrito ao eixo é dada por , onde está em joules e está em metros. Determine a força associada a esta função energia potencial.
Ver solução completaQuestão 4
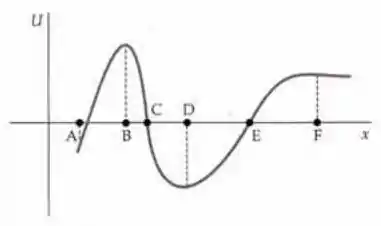
A figura mostra o gráfico de uma função energia potencial .
- Para cada ponto indicado, informa se a componente x da força associada a esta função é positiva, negativa ou zero.
- Em que ponto a força tem a maior magnitude?
Questão 5
Uma única força conservativa atua em uma partícula paralela ao eixo horizontal de um sistema de coordenadas. A energia potencial desta força é dada pela figura abaixo. Qual opção representa corretamente os vetores (direção, intensidade e sentido) das forças que atuam sobre a partícula nos pontos e respectivamente.
![]()
- diagrama 4
- diagrama 1
- diagrama 5
- diagrama 2
- diagrama 3
Questão 6
Um corpo de massa move-se ao longo de um eixo , em um movimento unidimensional, sob a ação exclusiva de uma força conservativa . Essa força conservativa está associada à função energia potencial dada por (as unidades são o joule e o metro):
a) Esboce o gráfico da função energia potencial.
b) Uma energia mecânica de é fornecida ao corpo. Encontre os pontos de retorno à esquerda, , e à direita, . Encontre também a velocidade escalar do corpo quando ele está na posição
c) A velocidade escalar do corpo vale no ponto . Qual a energia mecânica associada ao sistema? E em que ponto a velocidade do corpo assumirá o valor ?
Ver solução completaQuestão 7
Uma partícula de massa está submetida a um campo de força conservativa em uma dimensão conforme o gráfico abaixo. A energia potencial nesse campo, :
- É constante e igual a para ;
- Decresce linearmente entre e, onde seu valor é (trecho linear);
- Permanece constante entre e (trecho constante);
- É dada por: para (trecho parabólico);
Sendo a partícula abandonada em repouso no ponto :
- Calcule a energia mecânica da partícula e superponha seu gráfico como função
de ao gráfico do potencial.
b) Calcule o máximo valor de alcançado pela partícula em seu movimento subsequente
e indique no gráfico.
c) Obtenha a expressão para a energia cinética em função de e faça seu gráfico no espaço
apropriado entre os limites inferior e superior que a partícula pode atingir.
d) Obtenha a expressão e faça o gráfico da componente da força que age sobre a partícula
devido a esse potencial em função da posição entre os limites inferior e superior que a partícula
pode atingir.
e) Suponha agora que, ao ser abandonada a partícula nesse campo, seja adicionada uma
força de atrito de módulo constante , contrária ao movimento (por exemplo, atrito
com uma superfécie paralela ao eixo x). Faça o gráfico de para esta nova situação (superposto ao de U(x)), e determine o novo valor máximo de alcançado pela partícula.
Ver solução completaQuestão 8
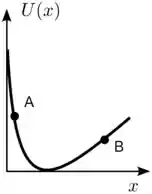
Uma partícula de massa se move sob a ação de um potencial unidimensional . Vide figura. Sabe-se que em a velocidade da partícula é . Determine a velocidade da partícula em .
Questão 9
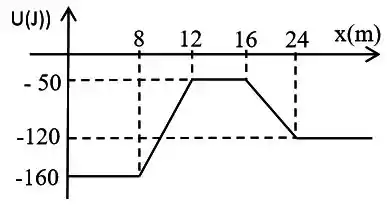
2 – Considere uma partícula que se move no eixo sob ação de uma força e que possui energia potencial em função da posição que varia de acordo com o gráfico abaixo. A energia mecânica da partícula é constante. Classifique as afirmações como verdadeiras ou falsas e justifique sucintamente, com apenas uma frase.
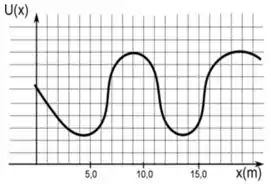
a) A força que atua na partícula em é positiva.
b) Em torno de , a força que atua na partícula é atrativa.
c) A energia cinética da partícula em é menor que a energia cinética da partícula em .
d) A força que atua na partícula em é não conservativa.
Ver solução completaQuestão 10
Uma partícula de massa 1,00 kg move-se ao longo do eixo x na região em que a energia potencial U(x) varia conforme a figura. Quando a partícula se encontra em x =20,0 cm, sua velocidade é de -2,00 m/s.
Determine o intervalo onde ocorre o movimento da partícula.
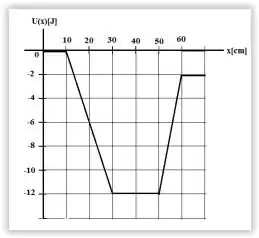
A) 12 ≤ x(cm) ≤ 60
B) 20 ≤ x(cm) ≤ 55
C) 16 ≤ x(cm) ≤ 57
D) 23 ≤ x(cm) ≤ 54
E) 16 ≤ x(cm) ≤ 24
Ver solução completaQuestão 11
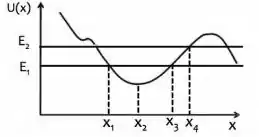
A figura mostra a energia potencial U(x) de uma partícula que se move ao longo do eixo x sob a ação da força resultante associada a U(x). Sabendo-se que a energia mecânica E é maior que U() e menor que U(), a alternativa FALSA é:
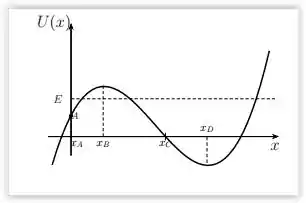
- o sentido da força na posição é positivo
- o sentido da força na posição é positivo
- na posição a força é nula
- caso a partícula passe pela posição , sua energia cinética nesse ponto é máxima
- a partícula não pode estar na posição
- caso a partícula passe pelo ponto , no deslocamento do ponto para o ponto , o trabalho realizado pela força é positivo.
(b) na posição a força é nula
(c) caso a partícula passe pela posição , sua energia cinética nesse ponto é máxima
(d) a partícula não pode estar na posição
(e) caso a partícula passe pelo ponto , no deslocamento do ponto para o ponto , o trabalho realizado pela força é positivo
Passo 1
Vamos analisar cada uma das afirmativas:
Começando pela primeira alternativa:
A gente sabe da relação entre força externa e energia potencial:
Na posição , nós vemos que a derivada do gráfico é positiva, logo é negativa, o que implica num sentido negativo.
Afirmativa é falsa.
Passo 2
Vamos aplicar novamente
No caso da posição , a derivada é nula, logo .
Afirmativa verdadeira,
Passo 3
Vamos entender essa afirmativa por meio do conceito de conservação da energia mecânica. A energia potencial se transforma em energia cinética e vice-versa, mas a soma das duas que é a energia total do sistema se conserva.
No ponto , a partícula está no ponto mínimo de energia potencial, logo é o ponto de energia cinética máxima.
Afirmativa verdadeira.
Passo 4
A energia mecânica total de se um sistema se dá pela soma da energia cinética com a energia potencial.
A energia potencial do ponto é maior do que a energia mecânica total, o que não pode acontecer devido à equação mostrada acima.
Afirmativa verdadeira.
Passo 5
Pelo teorema trabalho energia cinética, a gente sabe que:
Já vimos também quanto maior a energia potencial, menor a energia cinética, logo no ponto a energia cinética é menor do que no ponto .
Assim, sabemos que e, portanto, o trabalho é positivo.
Afirmativa verdadeira.
Ver solução completaQuestão 12
(Cap 6 – Ex 24) Uma caixa de 6,0 kg é levantada de uma altura de 3,0 m, a partir do repouso, por uma força aplicada vertical de 80 N. Encontre (a) o trabalho realizado sobre a caixa pela força aplicada, (b) o trabalho realizado sobre a caixa pela gravidade e (c) a energia cinética final da caixa.
Ver solução completaQuestão 13
Uma partícula de massa se movendo no eixo está sujeita a uma única força, cuja energia potencial é dada na figura abaixo. Quando passa pela posição , a velocidade da partícula é .
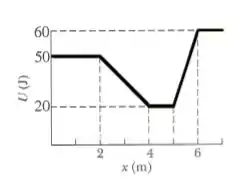
(a) Qual é o módulo e o sentido da aceleração da partícula no ponto ?
(b) A partícula chega ao ponto ? Em caso afirmativo, qual é a velocidade da partícula nesse ponto? Caso contrário, qual é o ponto de retorno entre e ?
(c) Considere agora que a partícula se move de até . Qual é o trabalho realizado pela força?
Ver solução completaQuestão 14
Uma partícula de massa se move ao longo de um eixo sob a ação de uma única força que é conservativa. A energia potencial associada a essa força está representada no gráfico ao lado. No ponto , a velocidade da partícula é .
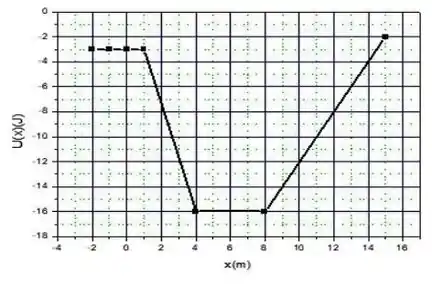
(a) Encontre o módulo e o sentido de em .
(b) Obtenha a energia mecânica dessa partícula.
(c) Determine a energia potencial no ponto. NOTA: .
Ver solução completaQuestão 15
Uma partícula se desloca sobre o eixo sob ação de uma força resultante conservativa, cuja energia potencial está representada no gráfico a seguir. No instante inicial a partícula está no ponto . Considere duas situações distintas: na primeira ela possui energia mecânica e na segunda energia mecânica e sua velocidade inicial é no sentido positivo do eixo .
Comparando sempre as situações em que a energia mecânica é ou , qual das seguintes frases a seguir é verdadeira?
(a) Quando a partícula está na posição a força sobre ela é a mesma nos dois casos.
(b) Quando a partícula está na posição a sua velocidade é a mesma nos dois casos.
(c) Em ambos os casos, a posição é um ponto de retorno.
(d) Na posição a força sobre a partícula é nula apenas no caso em que a energia mecânica é .
(e) A posição é uma posição em que a energia cinética é máxima, no caso em que a energia mecânica é .
Ver solução completaQuestão 16
O movimento de uma partícula é descrito pela seguinte energia potencial:
onde é medido em Joules e em metros. A força sobre a partícula é nula nos pontos:
(a) e .
(b) e .
(c) e .
(d) e .
(e) e .
Ver solução completaQuestão 17
Uma partícula de massa m = 2,0 kg move-se ao longo do eixo x sujeita a uma única força F. A dependência de F com a posição x da partícula é mostrada na Figura 1. A energia potencial associada à forçaa F é U. Quando a partícula está em x = 0, ela tem velocidade = 2,0 m/s no sentido positivo do eixo x.
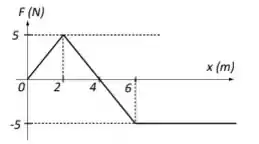
Em qual posição a partícula para momentaneamente antes de retornar?
a) 2,0 m
b) 2,8 m
c) 3,8 m
d) 4,0 m
e) 5,8 m
f) 6,0 m
g) 7,0 m
h) 7,8 m
i) 8,0 m
Ver solução completaQuestão 18
Se investigarmos o movimento dos átomos de uma molécula diatômica como o , veremos que eles executam um movimento vibracional. Porém, esse movimento não acontece para qualquer valor da energia mecânica, , dos átomos já que é possível dissociar a molécula. Levando em conta essas informações, podemos dizer que o movimento desses átomos pode ser descrito muito bem por uma energia potencial (sendo distância relativa entre os átomos), onde para e para , como a mostrada na figura abaixo.
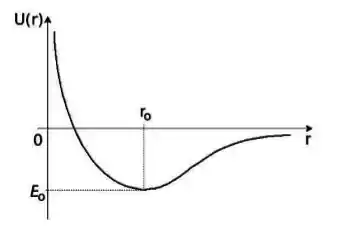
Considerando a energia potencial, podemos dizer que a força entre os átomos da molécula de é
Negativa quando e positiva para .
Positiva para e negativa quando .
Negativa para e positiva para .
Positiva sempre que .
Negativa sempre que .
Ver solução completaQuestão 19
Um objeto de massa igual a 2 kg apoiado em uma superfície horizontal sem atrito está preso a uma mola de massa desprezível que não obedece á Lei de Hooke. Ao ser comprimida ou esticada de uma posição x (em relação à sua posição de equilíbrio), a mola exerce uma força restauradora , onde k = 60 N/m e b = 18N/m². O objeto é puxado para a direita (na direção de x positivo), esticando a mola até uma distância de e a seguir é liberado. A energia mecânica E do objeto é dada por
a) E = 39 J
b) E = 78 J
c) E = 36 J
d) E = 18 J
e) E = 72 J
Ver solução completaQuestão 22
Na figura abaixo é apresentado o comportamento de uma curva de energia potencial (cuja unidade é o ) como função da posição. Além disso, quando . Se uma partícula se encontra em repouso no único ponto de equilíbrio estável, qual energia mínima deve ser fornecida para que a partícula descreva um movimento não confinado?
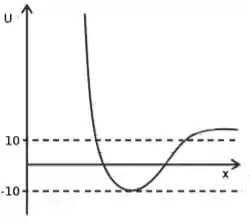
Ver solução completa
Questão 23
Uma partícula está submetida ao potencial mostrado.
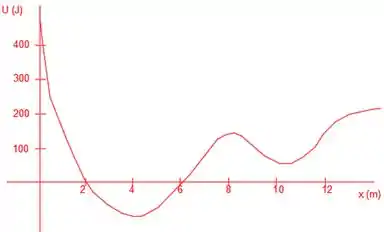
a) Faça o gráfico da força associada a esse potencial no intervalo de a.
b) Quais são os pontos de equilíbrios estável e instável? Justifique.
c) Se a partícula possui energia mecânica total igual a zero, em que intervalo no espaço ela pode ser encontrada? E se a sua energia total for ? Justifique.
d) Se sua energia total for de , qual sua velocidade no ponto ? Justifique.
Ver solução completaQuestão 24
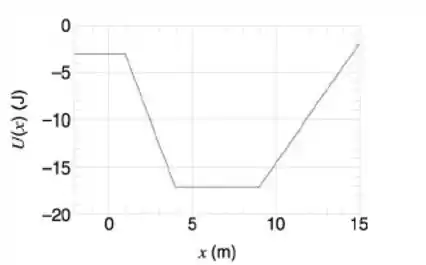
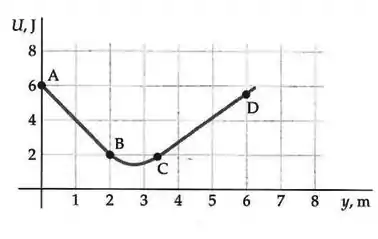
O gráfico abaixo mostra a energia potencial em função da distância de um objeto em movimento ao longo do eixo x. Em qual dos pontos marcados a força que age sobre o objeto tem a maior módulo?
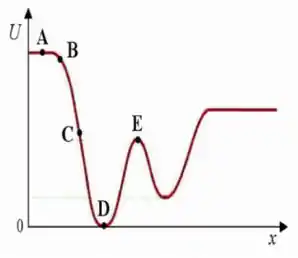
a) ponto A
b) ponto B
c) ponto C
d) ponto D
e) ponto E
Ver solução completaQuestão 25
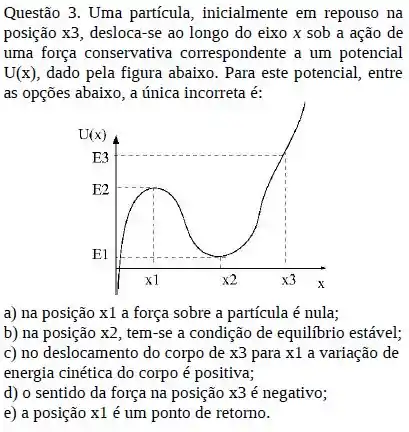
Um potencial unidimensional é mostrado na figura abaixo. Uma partícula sujeita a este potencial tem energia mecânica total E. Assinale a alternativa incorreta.
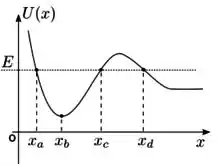
- A força agindo no ponto é negativa.
- A velocidade da partícula se anula em
- A força agindo na partícula no ponto é nula.
- A energia cinética da partícula é máxima entre e
- A posição é um ponto de retorno.
Questão 26
Uma partícula de massa se move sob a ação de várias forças conservativas e de uma força não conservativa. A energia potencial total em Joules associada às forças conservativas em função da posição em metros é dada pelo gráfico abaixo. Na posição a velocidade da partícula é . No trecho entre e , a força não conservativa realiza trabalho de .
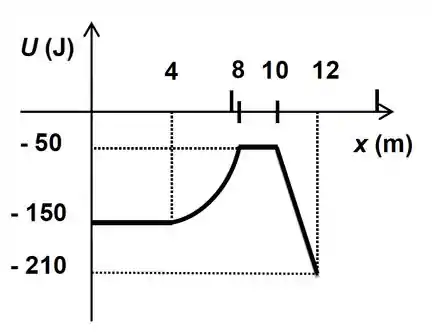
Obtenha a velocidade da partícula em .
Ver solução completaQuestão 28
Ainda sobre o gráfico da questão anterior, determine o sentido e a intensidade da força sobre a partícula na posição x = 20,0 cm.
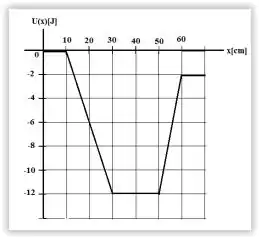
A) 6 N no sentido negativo.
B) 60 N no sentido negativo.
C) 6 N no sentido positivo.
D) 60 N no sentido positivo.
E) 12 N no sentido positivo.
Ver solução completaQuestão 29
. Dada uma função de energia potencial , a força correspondente está na direção
positiva do eixo x se:
é positiva
é negativa
é uma função crescente de
é uma função decrescente de
é impossível obter a direção de a partir de
Ver solução completaQuestão 30
Uma mola exerce uma força restauradora em um bloco de massa , da forma , onde e é a distância ao ponto de equilíbrio da mola. Se a mola for comprimida em , a velocidade com que o bloco passa pelo ponto de equilíbrio é:
Ver solução completa
Questão 31
A figura mostra a energia potencial U(x) de uma partícula que se move ao longo do eixo x sob a ação da força resultante associada a U(). Sabendo-se que a energia mecânica E é maior que U() e menor que U(), a alternativa incorreta é:
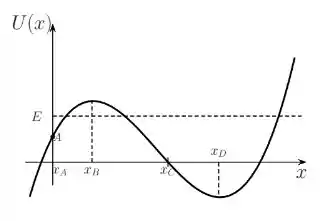
a) O sentido da força na posição é positivo
b) Na posição a força é nula
c) Caso a partícula passe pela posição , sua energia cinética nesse ponto é máxima
d) A partícula não pode estar na posição
e) caso a partícula passe pelo ponto , durante o deslocamento do ponto até o ponto , o trabalho realizado pela força é positivo
Ver solução completaQuestão 32
Uma força atuando sobre uma partícula varia de acordo com o gráfico abaixo. Calcule o trabalho realizado sobre a partícula quando ela se move de até .
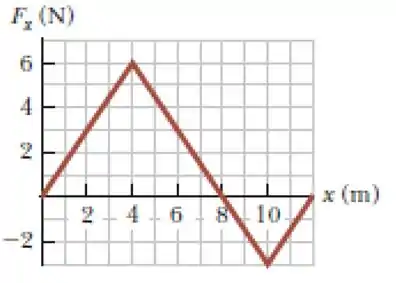
Ver solução completa
Questão 34
(Cap 6 – Ex 23) Encontre a energia cinética de (a) uma bola de beisebol de 0,145 kg movendo-se a uma velocidade de ; e (b) um corredor de 60,0 kg correndo a um ritmo constante de .
Ver solução completaQuestão 35
(Cap 6 – Ex 25) Uma força constante de 80 N atua sobre uma caixa de 5,0 kg. A caixa está, inicialmente, se movendo a 20 m/s no sentido da força e, 3,0 s depois, ela se move a 68 m/s. Determine o trabalho realizado por esta força e a potência média por ela desenvolvida durante o intervalo de 3,0 s.
Ver solução completaQuestão 36
Indique o ponto do gráfico ao lado, onde a força que atua sobre a partícula é negativa.
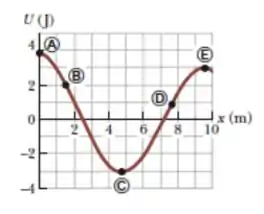
Ver solução completa
Questão 37
(Cap 6 – Ex 27) Uma partícula de 3,0 kg, que se move ao longo do eixo x, tem uma velocidade de +2,0 m/s quando passa pela origem. Ela está sujeita a uma força única, , que varia com a posição como mostrada na figura abaixo. (a) Qual é a energia cinética da partícula quando ela passa pela origem? (b) Qual é o trabalho realizado pela força, enquanto a partícula se move de x = 0,0 m até x = 4,0 m? (c) Qual é a rapidez da partícula quando ela está em x = 4,0 m?
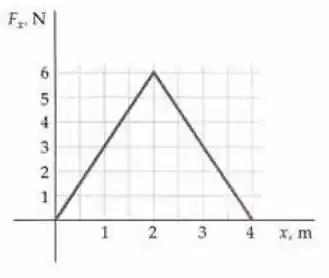
Questão 38
(Capítulo 7 – Problemas Adicionais – Exercício 54) Um bloco de é deixado cair em uma mola vertical, inicialmente relaxada, cuja constante elástica é (Fig. 7-44). O bloco fica acoplado à mola, comprimindo-a em até parar momentaneamente. Nessa compressão, que trabalho é realizado sobre o bloco (a) pela força gravitacional e (b) pela força elástica? (c) Qual é a velocidade do bloco imediatamente antes de se chocar com a mola? (d) Se a velocidade no momento do impacto é duplicada, qual é a compressão máxima da mola?
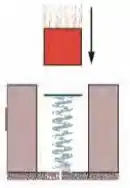
Questão 39
. Considere que uma bola de massa é abandonada do repouso de uma altura , e
retorna, após quicar no chão, a uma altura . Considerando a altura referência para o cálculo da energia potencial como sendo a superfície do planeta terra, o trabalho exercido pelas forças dissipativas neste problema é igual a
Um quarto da energia potencial gravitacional inicial
Metade da energia potencial gravitacional inicial
Três quartos da energia potencial gravitacional
Um terço da energia potencial gravitacional
Todas as outras alternativas estão incorretas
Ver solução completaQuestão 40
A energia potencial de uma partícula de massa numa dada posição é descrita pela função (em Joules, sendo em metros), mostrada na figura abaixo.
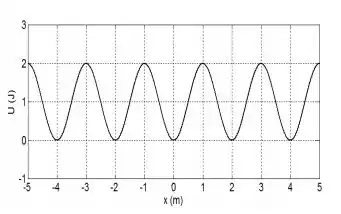
- Calculo a força que atua na partícula para todo .
- Calcule a frequência angular de pequenas oscilações em torno de .
- A posição em função do tempo.
- A velocidade em função do tempo da partícula, .
- O módulo da velocidade da partícula quando esta se encontra na posição .
Considerando que a partícula é colocada em repouso na posição no instante de tempo e realiza pequenas oscilações em torno de , determine:
Sugestão: utilize a série de Taylor de em torno de .
Ver solução completaQuestão 41
3) Uma partícula se move ao longo do eixo sob a ação de uma força total dependente apenas da posição e cujo gráfico está ilustrado na figura. Em , a partícula está na origem e tem velocidade . Ao atingir a posição , ela tem velocidade nula. Nessas condições, ao obtermos o módulo da velocidade da partícula na origem em termos de e encontraremos:
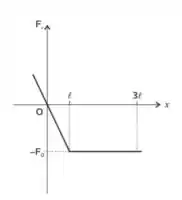
a)
b)
c)
d)
e)
Ver solução completaQuestão 42
Um corpo descreve um movimento retilíneo ao longo do eixo sob ação de uma única força conservativa. O gráfico da energia potencial do corpo em função de é mostrado na figura .
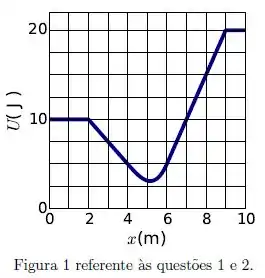
Pode-se concluir que a componente da força que age sobre o corpo em é igual a:
Questão 43
Dada uma função de energia potencial U(x), a força correspondente está na direção positiva do eixo x se:
a) é impossível obter a direção de a partir de U
b) U é uma função crescente de x
c) U é uma função decrescente de x
d) U é positiva
e) U é negativa
Ver solução completaQuestão 44
Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força conservativa, cuja energia potencial é mostrada na Figura 1. Inicialmente, a partícula encontra-se na posição com velocidade . Não existem forças dissipativas.
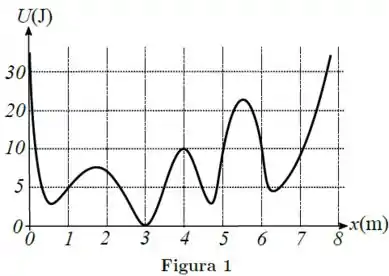
Ao passar pela posição , a velocidade da partícula é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 46
Um corpo é submetido a uma força conservativa cuja energia potencial associada apresenta o comportamento apresentado no gráfico
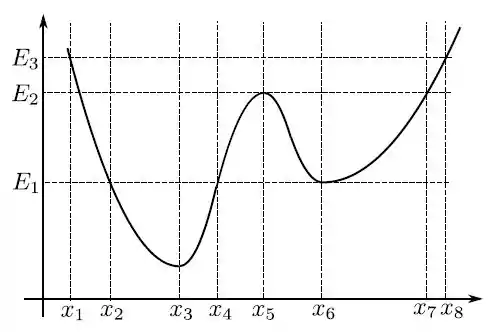
A respeito deste sistema são feitas as seguintes afirmações:
I. , e são pontos de equilíbrio estável.
II. Para uma partícula abandonada em , os pontos e são pontos de retorno.
III. Nos pontos de retorno a velocidade é nula, logo são pontos de equilíbrio.
IV. Uma partícula que parte de com energia se move apenas entre os pontos e .
Marque a opção que indica aquelas que são CORRETAS:
(a) Somente II
(b) Somente II e IV
(c) Somente II, III e IV
(d) Somente I, II e IV
(e) Somente I, III e IV
(f) Todas
Ver solução completaQuestão 47
Uma partícula move-se ao longo do eixo x sob a ação de uma única força conservativa, que dá origem à energia potencial
onde é medido em metros e é medido em joules. O trabalho, em Joules, realizado pela
força quando a partícula se movimenta de até é:
Ver solução completaQuestão 48
Se a energia potencial relacionada a uma força aplicada em um bloco pode ser expressa por , onde e são constantes, podemos dizer que a força tem a forma:
constante
nenhuma das outras respostas.
Ver solução completaQuestão 49
Considere o gráfico de energia de uma partícula em função de sua posição , onde é a energia total e é a energia potencial. A região do gráfico onde o movimento da partícula é possível é:
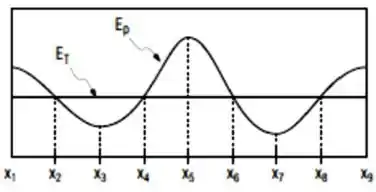
Ver solução completa
Questão 50
Considere que um corpo percorrendo uma trajetória retilínea no sentido positivo do eixo , cuja energia potencial em função de é mostrada na figura abaixo, tenha, em , energia cinética igual a .
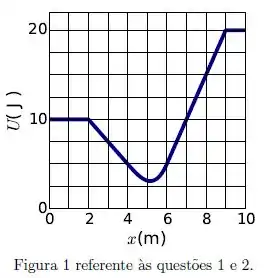
O ponto de retorno do corpo se encontra no intervalo:
Questão 51
Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força conservativa, cuja energia potencial é mostrada na Figura 1. Inicialmente, a partícula encontra-se na posição com velocidade . Não existem forças dissipativas.
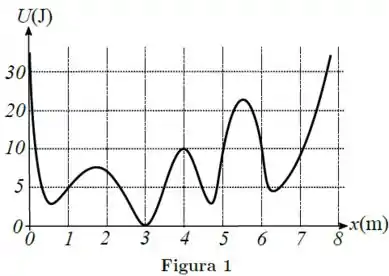
Considere as afirmativas abaixo:
(I) A força em é positiva (isto é, no sentido positivo do eixo ).
(II) O trabalho realizado pela força entre e é positivo.
(III) A variação da energia mecânica entre e é negativa.
Marque a alternativa que contém apenas afirrmativa(s) verdadeira(s).
(a) I
(b) II
(c) III
(d) I e II
(e) I e III
(f) II e III
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 52
Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força conservativa, cuja energia potencial é mostrada na Figura 1. Inicialmente, a partícula encontra-se na posição com velocidade . Não existem forças dissipativas.
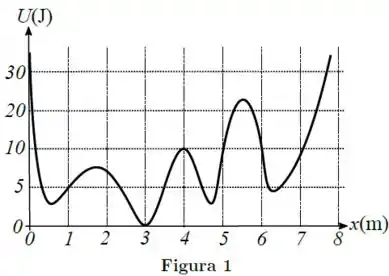
Além de um ponto de retorno no intervalo, em que a energia cinética da partícula é nula, há também um outro ponto de retorno no intervalo (em metros):
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 53
Considere uma partícula de massa que pode se mover somente ao longo do eixo , sujeita a apenas uma força conservativa , nessa direção, com energia potencial representada no gráfico abaixo. Não existem forças dissipativas. Inicialmente a partícula se encontra na origem, movendo-se no sentido negativo de , com velocidade . O trabalho realizado pela força quando a partícula se desloca de um ponto até um ponto é denotado por .
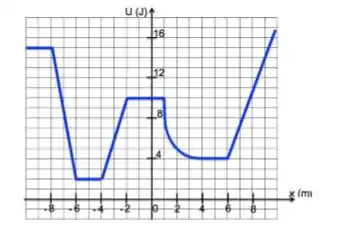
Assinale a alternativa correta:
(a) Em e.
(b)
(c) Em , e .
(d)
(e) Em , e .
(f) Em , e .
(g) Em , e independe de .
(h) Em , e .
Ver solução completaQuestão 54
Uma partícula se move sobre o eixo sob a ação exclusivamente de uma força conservativa, cuja energia potencial associada está indicada na figura. A reta pontilhada horizontal indica a energia mecânica da partícula. É INCORRETO afirmar que
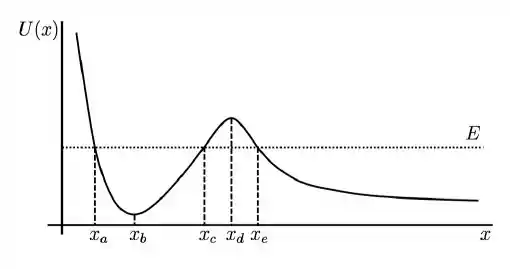
a) Se a partícula está inicialmente no ponto , seu movimento é oscilatório entre os ponto e
b) A velocidade da partícula é nula nos pontos , e
c) Os pontos e são pontos de equilíbrio estável e instável, respectivamente
d) A força que atua sobre a partícula aponta no sentido positivo de se a partícula se encontra à direita do ponto
e) O trabalho realizado sobre a partícula em um deslocamento de para é negativo.
Ver solução completaQuestão 55
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força , cuja energia potencial associada, , está representada no gráfico ao lado. Os trechos e s’ao retos. A energia da partícula é . Quando a partícula passa pela posição , sua rapidez e a força sobre ela valem
(a) ;
(b) ;
(c) ;
(d) ;
(e) ;
Questão 56
Uma partícula de massa m = 2,0 kg move-se ao longo do eixo x sujeita a uma única força F. A dependência de F com a posição x da partícula é mostrada na Figura 1. A energia potencial associada à forçaa F é U. Quando a partícula estáa em x = 0, ela tem velocidade = 2,0 m/s no sentido positivo do eixo x.
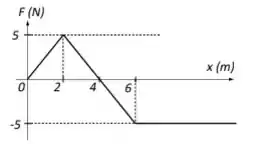
Considere as afirmativas:
I. No intervalo 0 ≤ x ≤ 4,0 m, a velocidade da partícula é máxima em x = 2,0 m.
II. A variação da energia potencial ∆U entre x = 0 e x = 2,0 m é positiva.
III. O trabalho realizado pela força F entre x = 2,0 m e x = 4,0 m é negativo.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
a) I
b) II
c) III
d) I e II
e) I e III
f) II e III
g) Todas
h) Nenhuma
Ver solução completa