Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 70

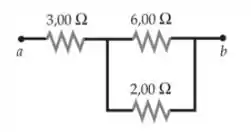
Se a queda de potencial entre os pontos a e b (Figura 25-53) é 12   V , determine a corrente em cada resistor.

Passo 1

Faaaaaaaala meu caro, tudo certinho?

Vamos simplificar o problema substituindo primeiro os resistores que estão em paralelo por sua resistência equivalente.

Podemos então adicionar essa resistência (conjunto) e a resistência de 3,00 Ω para encontrar a resistência equivalente entre os pontos a e b.

Marcamos as correntes através de cada resistor correspondentes à resistência através da qual a corrente acontece, aplicaremos a lei de Ohm para encontrar essas correntes.

A resistência equivalente dos dois resistores em paralelo e resolva para R e q , 1 :

1 R e q , 1 = 1 R 6 + 1 R 2 = 1 6 Ω + 1 2 Ω

R e q , 1 = 1,50   Ω

Como o resistor de 3,00 Ω está em série com R e q , 1 :

R e q = R 3 + R e q , 1 = 3 Ω + 1,5 Ω

R e q = 4,5   Ω

Aplicando a lei de Ohm à rede para encontrar I 3 :

I 3 = V a b R e q = 12 V 4,5 Ω = 2,667   A

I 3 = 2,667   A

Encontrando a diferença de potencial entre os resistores paralelos:

V 6 & 2 = V a b - V 3

V 6 & 2 = 12 V - ( 2,667 A ) ( 3 Ω )

V 6 & 2 = 3,997   V

Use a diferença de potencial comum entre os resistores em paralelo para encontrar a corrente através de cada um deles:

I 6 = V 6 R 6 = 3,999   V 6   Ω = 0,667 A  

I 6 = V 6 & 2 R 6 = 3,999   V 2   Ω = 2   A

Resposta

I 6 = 0,667   A

I 2 = 2   A

I 3 = 2,67   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o circuito mostrado na Figura 25-65, encontre a diferença de potencial entre o ponto a e o ponto b.
No circuito da Figura 25-61, a leitura do amperímetro é a mesma quando ambas as chaves estão abertas e quando ambas as chaves estão fechadas. Qual é a resistência desconhecida R?
Duas baterias idênticas, cada uma tendo um emf ε e uma resistência interna r, podem ser conectadas através de uma resistência R com as baterias conectadas em série ou em paralelo. Em cada situação, de
No circuito mostrado na Figura 25-63, as baterias têm resistência interna desprezível. Encontre (a) a corrente em cada ramificação do circuito, (b) a diferença de potencial entre o ponto a e o ponto b
No circuito mostrado na Figura 25-62, as baterias têm resistência interna insignificante. Encontre (a) a corrente em cada ramal do circuito, (b) a diferença de potencial entre o ponto a e o ponto b, e