Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.Problemas Adicionais - Ex. 103
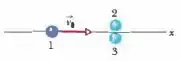
As três bolas vistas de cima na Fig. 9-76 são iguais. As bolas 2 e 3 estão se tocando e alinhadas perpendicularmente à trajetória da bola 1. A velocidade da bola 1 tem módulo e está dirigida para o ponto de contato das bolas 2 e 3. Após a colisão, quais são (a) o módulo e (b) a orientação da velocidade da bola 2, (c) o módulo e (d) a orientação da velocidade da bola 3 e (e) o módulo e (f) a orientação da velocidade da bola 1? (Sugestão: sem atrito, cada impulso está dirigido ao longo da reta que liga os centros das bolas envolvidas
na colisão e é perpendicular às superfícies que se tocam.)
Passo 1
Então galera , bora dar uma olhada na figura que ilustra o problema :
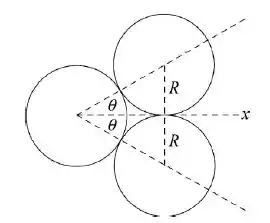
A bola incidente exerce um impulso de mesmo módulo sobre as outras duas bolas, ao longo da reta que liga o centro da bola incidente ao centro da bola que sofre o choque. As bolas que sofrem o choque se afastam ao longo dessas retas, enquanto a bola incidente continua a se mover ao longo do eixo . Analisando a figura , observamos que os ângulos assinalados na figura valem . Como a componente do momento total do sistema de três bolas é conservada, temos que :
Passo 2
Bom pessoal , como a energia cinética total é conservada, temos que :
A primeira equação nos dá ; elevando ao quadrado, obtemos que:
Substituindo na segunda equação e explicitando , obtemos
De acordo com o cálculo acima, o módulo da velocidade da bola 2 é .
Passo 3
Bom galera , como percebemos no item anterior , sabemos que a velocidade da bola 2 faz um ângulo de no sentido anti-horário com o semieixo x positivo.
Passo 4
A velocidade da bola 3 , por sua vez , é o mesmo da bola 2 e vale .
Passo 5
Bom galera , usando um raciocício análogo aos dos itens anteriores , sabemos que a velocidade da bola 3 faz um ângulo de no sentido horário com o semieixo positivo.
Passo 6
Então pessoal , podemos usar a equação do momento para calcular a velocidade final da bola 1:
Assim, o módulo da velocidade da bola 1 é .
Passo 7
Reparem que o sinal negativo mostra que, após o choque, a bola 1 se move no sentido negativo do eixo .
Resposta
Respectivamente :
a velocidade da bola 2 faz um ângulo de no sentido anti-horário com o semieixo x positivo.
a velocidade da bola 3 faz um ângulo de no sentido horário com o semieixo x positivo.
Após o choque a bola 1 se move no sentido negativo do eixo .
Tranquilo galera? Bora resolver mais questões então