Lei de Biot-Savart Geral
Produzido por Bruno SoaresTeoria
A Lei de Buit-Savart é utilizada para calcular o campo magnético
Agora vamos ver quem é essa tal de Lei de Biot-Savat e como que ela pode cair em exercícios! 😉
Lei de Biot-Savat: Fórmula
Vamos direto ao que interessa, a fórmula da Lei de Biot-Savat! Ela tem essa carinha aqui:

Na prática o que essa lei diz pra a gente?!
Uma corrente elétrica gera um campo magnético e cada carguinha da corrente elétrica contribui um pouco para o campo magnético gerado, certo?
Então a Lei de Biot-Savat soma o campo magnético infinitesimal gerado por cada carga elétrica e no final a gente tem o campo elétrico gerado pela nossa corrente!
Agora vamos ver quem é quem na Lei de Biot-Savat:
é a permeabilidade magnética no vácuo, igual a ; é a corrente elétrica; é a distância entre o corpo e o ponto onde estamos calculando o campo magnético ; - O vetor
é tangente ao fio, sempre no sentido da corrente; - O vetor unitário
aponta do fio para o ponto onde estamos calculando o campo magnético.
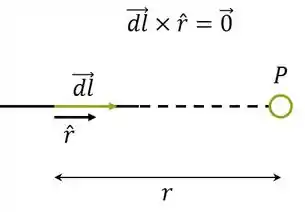
Pra ficar mais claro, vamos considerar esse fio semicircular, percorrido por uma corrente
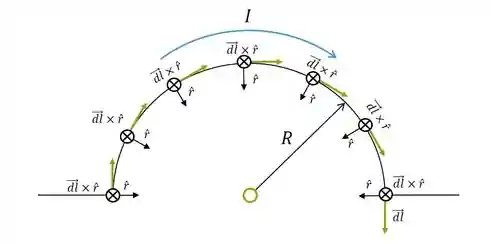
Reparou como o produto vetorial
📢 Clique para ver mais:
Beleza, mas como eu uso a Lei de Biot-Savat?!
Pra responder isso e muito mais, se liga nesse vídeo super completo que o Responde Aí preparou pra você! 🧡 👇
Exemplo: Calcule o Campo Magnético do segmento semicircular do fio no ponto P
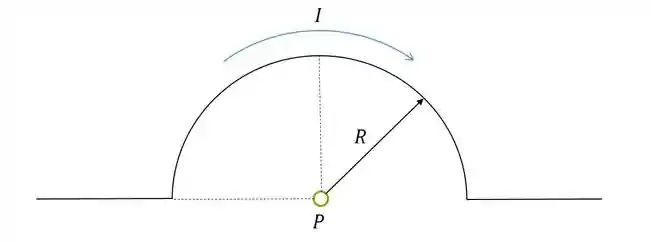
Primeiro vamos definir as coordenadas:
Aplicamos a Lei de Biot-Savat:
O vetor
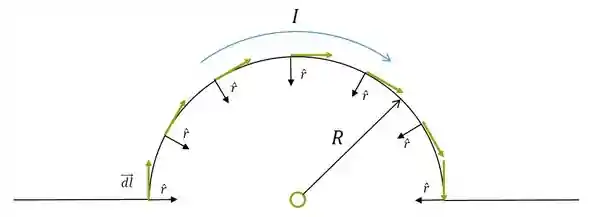
Temos a direção do produto vetorial:
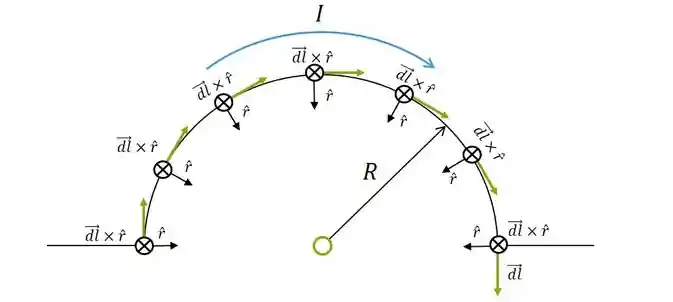
O ângulo
Substituindo na integral:
Sabemos que
Integrando temos:
Prontinho! Agora vamos praticar com exercícios?!
Exemplo: Calcule o Campo Magnético do segmento semicircular do fio no ponto P
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ – Prova 2 – 2012.1 – Múltipla Escolha nº9.
Considere o circuito da figura abaixo, constituído por segmentos retilíneos (I, III, V e VI) e segmentos de arco de círculos (II, IV e VII) concêntricos com o ponto , percorridos por uma corrente estacionária , com sentido assinalado. Indique quais de tais segmentos dão uma contribuição não nula para o campo magnético resultante no ponto .
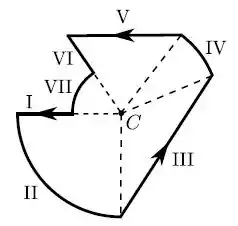
- II, III, IV, V e VII
- I, III, V e VI
- II, IV e VII
- I, II, IV, VI e VII
- Todos criam campo magnético não nulo em
Passo 1
O campo magnético de uma distribuição continua de corrente é dado pela Lei de Biot-Savart:
Para sabermos quais segmentos dão uma contribuição não nula para o campo magnético resultante do ponto C precisamos analisar o produto vetorial para cada segmento.
Passo 2
Para o segmento I os vetores e são antiparalelos, ou seja, formam um ângulo de e nesse caso:
Para o segmento VI os vetores e são paralelos, ou seja, formam um ângulo de 0° e nesse caso:
De maneira geral, podemos mostrar que segmentos retilíneos que estão alinhados na direção não contribuem para o campo, pois:
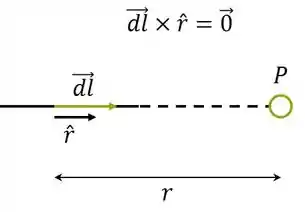
Desse modo, temos que os segmentos I e VI possuem contribuições NULAS para o campo no ponto C, assim já eliminamos as alternativas b, d, e.
Passo 3
Para os demais segmentos (II, III, IV, V e VII) os vetores e não estão alinhados de modo que:
Assim, o campo produzido por esses segmentos no ponto C é não nulo. Desse modo, eliminamos a letra c e já temos nossa resposta. =)
Resposta
Letra a
Exercício Resolvido #2
UFRJ – Prova 2 – 2012.2 – Múltipla Escolha nº8.
Dois fios muito longos são percorridos por correntes elétricas estacionárias de mesma intensidade. Cada um de tais fios é constituído por dois segmentos retilíneos (muito longos) e por um arco circular intermediário (com abertura de ); os raios de tais arcos são tais que . Qual dos segmentos dá maior contribuição para o campo magnético resultante no ponto central ?
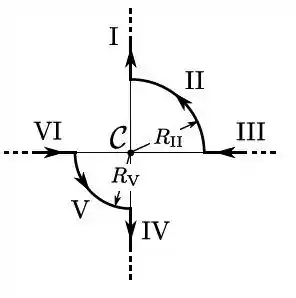
- II
- V
- I e III
- IV e VI
- Todos contribuem igualmente para .
Passo 1
Pela lei de Biot-Savart:
Primeiramente fazemos os produtos vetoriais dos fios retilíneos e mostramos que eles fazem campo nulo:
Passo 2
Agora vamos fazer os segmentos circulares. Sabemos que em cada um deles temos constante e a corrente também:
Seja o sentido saindo da tela. Fazendo o produto vetorial para um segmento semicircular genérico:
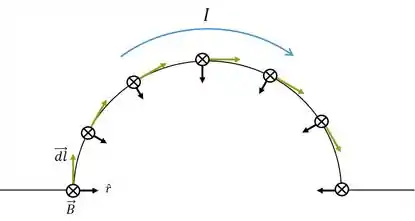
Temos:
O comprimento é um quarto de circunferência:
Passo 3
Portanto, para cada um dos segmentos temos:
Agora queremos saber quem dá mais. Como:
Segue:
Passo 4
Multiplicando ambos os lados por :
Ou seja, o segmento V é quem dá mais.
Resposta
Letra b
Exercício Resolvido #3
UFRJ – Prova 2 – 2013.1 – Múltipla Escolha nº2.
Uma corrente estacionária, de intensidade , flui ao longo de um segmento retilíneo que se divide, igualmente, em quatro meridianos de uma esfera de raio , perpendiculares (dois a dois) entre si, e reencontrando-se num outro segmento retilíneo. Qual é o módulo do campo magnético no centro da esfera?
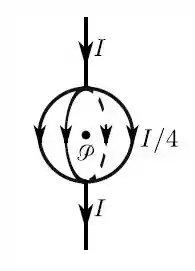
Passo 1
É a Lei de Biot-Savart que nos dá a fórmula para calcular campo magnético produzido por uma corrente né?
É ela que vamos usar!!
Mas pera, vamos analisar primeiro os segmentos retilíneos e depois os segmentos semicirculares, beleza?
Passo 2
Então bora analisar os segmentos retilíneos.
Para os dois segmentos retilíneos os vetores e , para o cálculo do campo no ponto P, estão alinhados, ou seja, o ângulo entre eles é ou . Para esses casos podemos mostrar que:
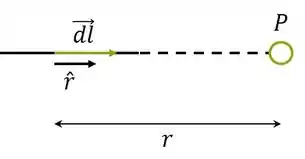
Então, os segmentos retilíneos não contribuem para o campo no ponto P.
Passo 3
Agora, nos resta analisar os segmentos semicirculares. Para achar o campo produzido por cada um desses segmentos no ponto P precisamos calcular essas quatro integrais.
SÉRIO?? :/
Calma! O truque neste caso é se aproveitar da simetria.
Vamos analisar primeiro o campo produzido por um par de segmentos semicirculares que estão um frente ao outro. Podemos aplicar a lei de Biot-Savart sobre todo o comprimento dos dois segmentos e teremos esse resultado:
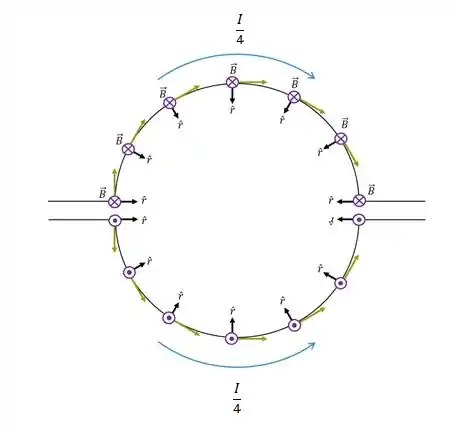
Pela figura podemos perceber que os campos produzidos por cada segmento possuem a mesma direção, mas sentidos opostos.
Note também que a corrente que passa pelos dois segmentos é a mesma, o comprimento dos dois segmentos é o mesmo e a distância dos segmentos para o ponto P também é a mesma, pois o ponto P é o centro da semicircunferência. Então nós temos que o módulo dos campos produzidos é o mesmo.
Então os campos se anulam e o campo resultante desse par será zero no ponto P.
Analogamente, o outro par vai zerar também.
Logo, o campo total é:
Resposta
Letra c
Exercício Resolvido #4
UFRJ – Prova 2 – 2014.1 – Múltipla Escolha nº2.
Calcule o campo magnético no ponto devido ao circuito com corrente estacionária de intensidade .
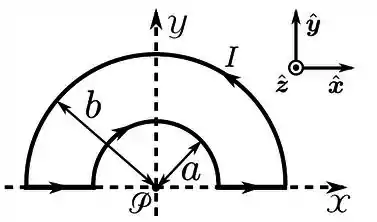
Passo 1
Bom, fio circular é com Biot-Savart. Enunciando a Lei:
Mostramos que os segmentos retilíneos não contribuem com campo pois o produto vetorial de dois vetores paralelos é nulo:
Passo 2
Agora vamos fazendo o produto vetorial para cada um dos segmentos semicirculares
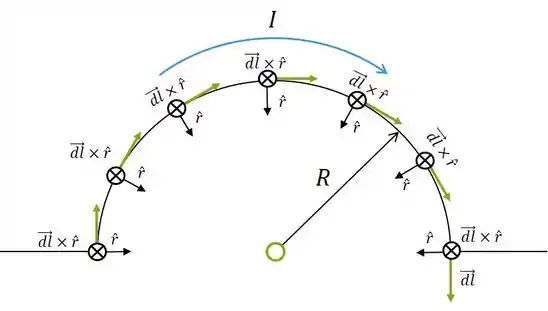
O menor fica:
Passo 3
Analogamente o maior fica:
Passo 4
Somando:
Arrumando:
Resposta
Letra a
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 262-88
Mostre que o módulo do campo magnético produzido no centro de uma espira retangular de comprimento e largura , percorrida por uma corrente é dado por:
Passo 1
A espira tem mais ou menos essa cara aqui:
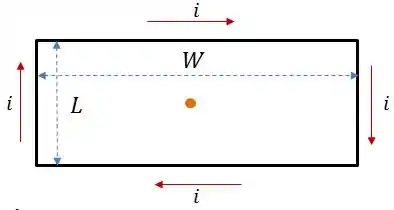
Pra resolver a nossa vida aqui, vamos usar a Lei de Biot-Savart, que nos diz que:
Vamos fazer o seguinte então... vamos calcular um campo magnético para o fio vertical e um campo magnético para o fio horizontal. Feito isso, é só multiplicarmos por dois.
Passo 2
Vou começar pelo fio vertical de comprimento . Vamos adotar a seguinte orientação:
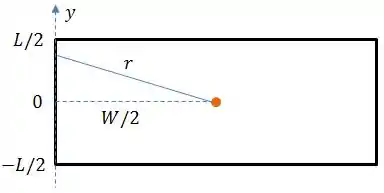
Dessa forma:
Agora precisamos resolver a parte do :
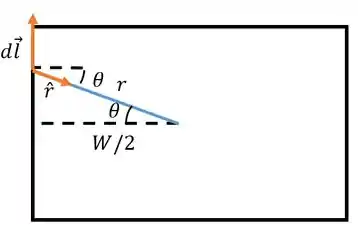
Vamos quebrar um pouco a cabeça aqui...
Ah! Como chamamos a direção vertical de , ao invés de usar , vou usar .
Geometricamente falando:
Ou seja:
Agora sim... montando a integral da Lei de Biot-Savart:
O módulo do campo vai ser então
Ajeitando isso aqui...
Passo 3
Então, agora nós faríamos para o fio horizontal... mas concorda que o raciocínio seria o mesmo? Trocando apenas o pelo ...
Seguindo o pensamento, para o fio horizontal:
Passo 4
Como se tratam de dois fios verticais e dois horizontais, o campo magnético resultante é dado por:
Vamos colocar o que der em M.M.C. pra tentar organizar essa bagaça...
Por último...
ACABOU!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Site do Prof. A. F. Guimarães, lista 09 de Física 3
O fio que aparece na figura abaixo é percorrido por uma corrente . Qual é o valor da contribuição para o campo magnético no centro da semicircunferência devido
(a) a cada segmento retilíneo de comprimento ;
(b) à semicircunferência de raio ; e
(c) a todo fio?
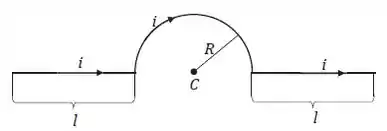
Passo 1
(a) Contribuição dos segmentos retilíneos de comprimento .
Aqui, vamos aplicar a lei de Biot-Savart, que é dada por:
Bem, vamos começar olhando para a figura abaixo:
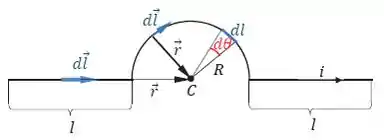
Daí a gente já consegue concluir que, tanto para o segmento retilíneo da esquerada, como para o da direita, temos que:
já que esses vetores são paralelos entre si. Isso significa que esses segmentos não contribuem para o campo magnético em .
Passo 2
(b) Contribuição da semicircunferência de raio .
Já para a semicircunferência, podemos concluir da figura que:
Substituindo na expressão de , temos:
Integrando:
Se usarmos a regra da mão direita para determinar direção e sentido do campo, vemos que ele é perpendicular ao plano da folha e aponta para dentro dela.
Passo 3
(c) Contribuição de todo o fio.
A contribuição total é a soma de todas as contribuições. Mas como o campo em gerado pelos dois segmentos de reta é nulo, o campo magnético total em vai ser aquele calculado no item (b), dado por:
Resposta
(a)
(b)
(c)
Exercício Resolvido #7
Site do Prof. A. F. Guimarães, lista 09 de Física 3
Determine o módulo do campo magnético de um fio retilíneo de comprimento , por onde passa uma corrente , num ponto situado a uma distância do fio. Dê a resposta em função dos ângulos e formados entre a normal ao fio baixada do ponto e pelas retas que unem o ponto com as extremidades do fio considerado.
Passo 1
A figura abaixo representa a configuração dada no enunciado.
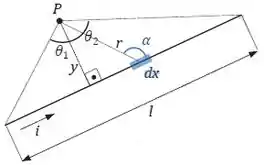
Vamos utilizar a lei de Biot-Savart para encontrar o campo magnético . Temos que:
já que o ângulo entre os vetores e é igual a .
Passo 2
Precisamos, agora encontrar uma relação de com o ângulo , já que os dois estão variando com . Para isso, vamos olhar para o triângulo retângulo abaixo:
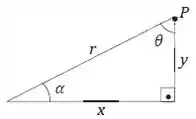
Da figura, a gente pode concluir que
E também que
Agora, precisamos relacionar o ângulo com o raio . Temos que:
Passo 3
Vamos substituir todas as relações encontradas no Passo 2 na expressão de :
Passo 4
Agora, já podemos integrar a expressão do Passo 3 para encontrar o módulo do campo magnético . Mas antes vamos checar os limites de integração. Se a gente olhar para as duas figuras, vemos que o ângulo varia, na verdade, de até . Serão esses, então, os nossos limites. Vamos lá:
Resposta
Exercício Resolvido #8
PUC Rio – Prova 2 – 2017.2 – Questão 2
Considere a espira da figura formada pelo arco de circunferência centrado em e raio , pelo segmento de comprimento sobre o eixo e pelo segmento paralelo ao eixo . A espira é percorrida por uma corrente de intensidade com sentido mostrado na figura (anti-horário).
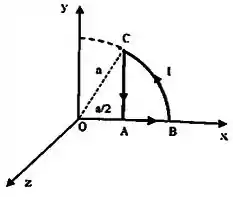
Nestas condições, utilizando explicitamente a Lei de Biot-Savart e justificando as suas afirmações, determine:
(a) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
(b) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
(c) O campo magnético (módulo, direção e sentido) na origem devido ao arco .
(d) O campo magnético total (módulo, direção e sentido) na origem .
Passo 1
(a) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
Bom, vamos lá. Para começar, vamos relembrar o que a lei de Biot-Savart nos diz. Temos:
onde o vetor aponta na direção da corrente e aponta para onde queremos medir o campo, respectivamente. Além disso, é a distância até o ponto no qual o campo será medido. Beleza? Vamos adiante.
Passo 2
No item (a), queremos medir o campo na origem gerado pelo segmento . Vamos olhar para a figurinha abaixo.
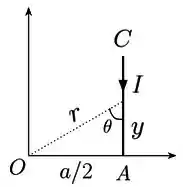
Bem, da figura, podemos concluir que a distância à origem de um elemento de corrente infinitesimal é dada por:
Vamos calcular também o seno de , para quando fizermos o produto vetorial . Temos:
Pra finalizar, vemos que é, na verdade, .
Passo 3
Agora podemos reescrever a equação de Biot-Savart com as informações que a gente obteve acima. Saca só:
O sentido e direção de podem ser obtidos pela regra da mão direita! Bem, como aponta para baixo e tem a direção da reta tracejada da figura, apontando para a origem, irá apontar para dentro da página, ou seja, no sentido negativo do eixo .
Passo 4
Por fim, para obter , integramos a equação acima. Lembrando que varia de até , que é o comprimento de . Temos:
Agora precisamos resolver essa integral! Para isso, fazemos a seguinte substituição de variáveis:
Para , e para , .
A integral resultante vai ser:
Passo 5
(b) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
Agora, vamos para o item (b). Nesse caso, os vetores e tem a mesma direção. Isso significa que , pois o seno do ângulo entre eles é nulo. Isso significa que
Passo 6
(c) O campo magnético (módulo, direção e sentido) na origem devido ao arco .
Agora só falta calcular a contribuição do arco , certo? Estamos quase lá! Nesse caso, a distância à origem é sempre constante e igual a . Além disso, o ângulo entre e é reto. Pela regra da mão direita, o campo na origem aponta para fora, no sentido positivo de .
Temos:
Passo 7
(d) O campo magnético total (módulo, direção e sentido) na origem .
O campo magnético total na origem será:
Resposta
(a)
(b)
(c)
(d)