Pêndulo Físico
Produzido por Leonardo de BemTeoria
Fala aii! Seja muito bem vindo ao RespondeAí, a gente esta aqui pra te ajudar a aprender tudo sobre as matérias de exatas, sem complicação!
Então bora bater um papo sobre o Pêndulo Físico?!
Muito provavelmente você já ouviu falar de pêndulo simples, mas hoje vamos aprender sobre um pêndulo um pouco diferente, o pêndulo físico!
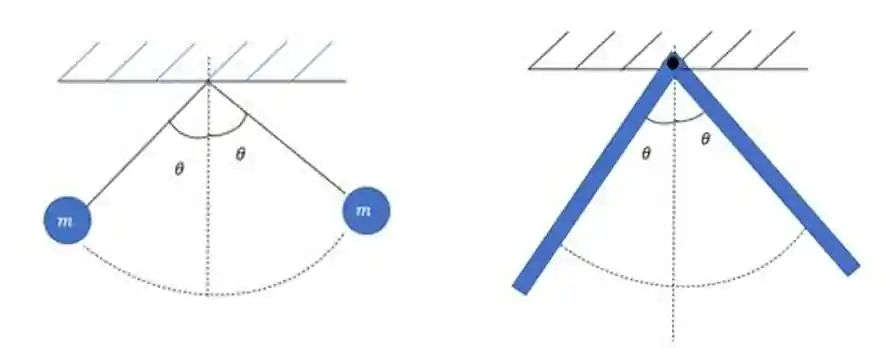
Na imagem a cima a gente tem dois pêndulos, um simples e um pêndulo físico. Eles são bem parecidos, mas qual é a principal diferença entre eles?
No caso do pêndulo simples a concentração de massa era em um ponto único, no caso da figura na bolinha. Já no pêndulo físico a barra tem massa distribuída ao longo do corpo, temos um corpo de massa
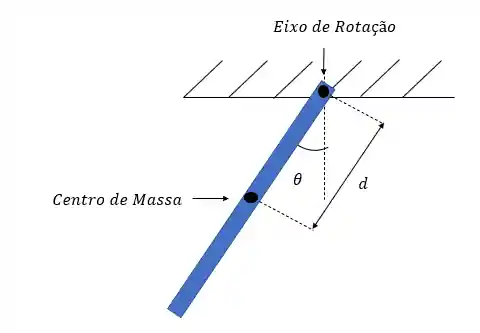
Aqui consideraremos toda a massa distribuída como uma massa resultante que colocaremos no centro de massa. Nas barras homogêneas o centro de massa está localizado no centro da barra nos outros casos a posição será dada ou calculada.
Beleza, entrou toda essa galera, mas e agora como eu calculo o período de um pêndulo físico com toda essa gente?
A gente vai usar essa equação aqui:
Mas, da onde saiu essa equação?! E como usamos ela?!
Calma...a gente já vai ver isso juntinho. E quando terminarmos você pode praticar nessa lista de exercício que preparamos especialmente pra você! 🧡
Período do Pêndulo Físico
O nosso objetivo aqui é encontrar a equação do período do pêndulo Físico!
Então vamos para um passo a passo!
Passo 1: Desenhar o diagrama de corpos livres
A primeira coisa que faremos é desenhar e analisar o diagrama de corpos livre com as forças atuantes.
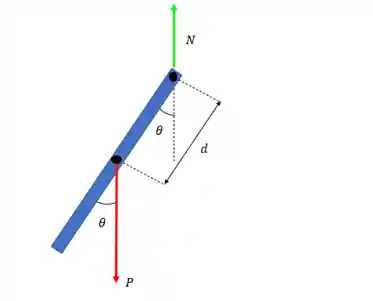
E usamos a segunda lei de newton pra rotação:
Onde
Vamos calcular o torque em relação ao ponto do eixo, ou seja, o ponto que não se move. Mas antes vamos decompor o peso em duas direções pois apenas em uma delas o peso vai gerar algum torque.
Vamos definir como
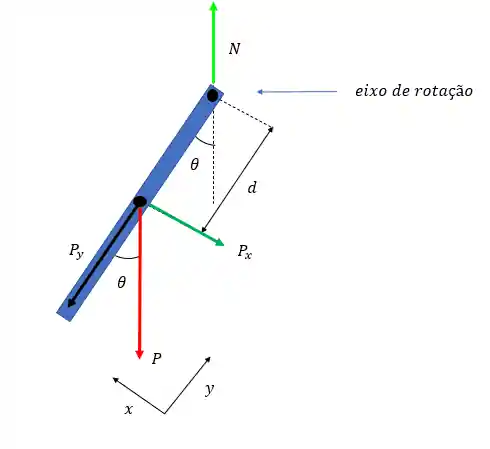
Passo 2: Encontrar torque resultante
Para isso vamos analisar o esquema a cima. Nele podemos perceber que a força normal está atuando em cima do eixo de rotação portanto pra ela a distância do eixo é
A força
E a única força que gera algum torque é o
O sinal negativo é dado pelo nosso referencial adotado.
Enfim podemos dizer que o torque gerado pela força peso em
Passo 3: Aplicar a Segunda Lei de Newton da rotação.
Que é já vimos lá em cima, mas relembrando:
Como
Para pequenos valores de
Então:
Pronto! Já está no formato da equação do MHS, lembra dela?
E como o sinal deu positivo, acertamos de primeira.
Comparando com a equação do MHS, a gente pode ver que:
Como a frequência angular que a gente conhece é dada por:
E enfim isolamos o período:
Exemplo:
Bom a gente aprendeu como calcular o período e a frequência angular do pêndulo físico, vamos ver se aprendemos mesmo?
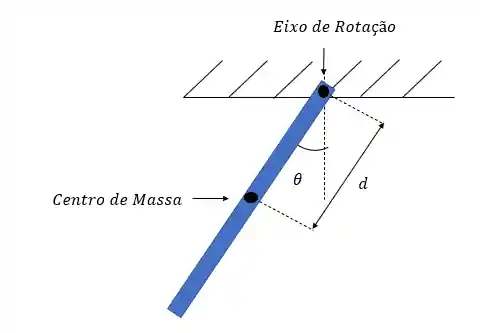
Se a nossa barra do exemplo for homogênea, possuir massa
Bom, aqui a gente já analisou a situação e vimos que a frequência angular é dada por:
Mas quem é a distância,
E o peso
Enfim falta pra nós o momento de inércia que para uma barra é dado por:
Porém no nosso caso o eixo do centro de massa está deslocado do eixo de rotação de uma distância
Então o momento de inércia fica:
Organizando e substituindo:
Substituindo na equação da frequência temos:
E como o período é dado por:
Encontramos o período de oscilação!
Poderíamos também fazer também com as equações e desenvolver mais um pouco para achar uma solução que não dependa da massa:
E enfim temos, pra esse caso a frequência angular independente da massa:
E o período também é independe da massa, basta usarmos:
Lembrando que essas equações independentes da massa foram deduzidas a partir do momento de inércia desse tipo de barra com o centro de massa no meio da largura
Pra encerrar eu vou te deixar com uma vídeo aula desse tópico!
Vamos exercitar?