Regime Transitório, Permanente e Ressonância
Produzido por Leonardo de BemTeoria
Vamos ver agora o que acontece quando além da força externa oscilatória ainda temos atrito!
Observe o sistema abaixo:
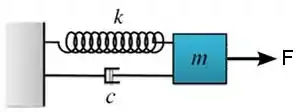
Existe uma força , externa, afetando o movimento, e um sistema que fornece atrito.
Então como ficaria a equação do movimento nesse caso?
Vamos, novamente, usar a segunda Lei de Newton. Antes disso, calculamos a força resultante:
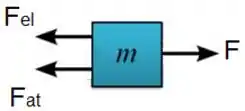
onde:
Então:
Segunda Lei de Newton:
Logo:
Fazendo as substituições de sempre, e , temos:
Não confunda , a frequência natural da mola (de valor constante ) com , a frequência da força externa, que tem valor variável!!
Show? Até aí tudo bem. No entanto, solucionar essa EDO não é tão simples.
Mas a gente pode tirar uma conclusão rápida: A solução da equação homogênea é uma equação de um MHA (que pode ser crítico, supercrítico ou subcrítico).
Pra se obter a solução particular a gente tem que usar uns métodos bizarros envolvendo números complexos. Porém isso não importa muito, é importante que você saiba que ela será do tipo:
Com:
E como você pode ver, a amplitude oscilação depende da frequência externa.
Eita! E o que isso nos diz? Nos diz que a solução particular é uma função oscilatória que oscila de acordo com a frequência da força externa, porém com uma diferença de fase, !
Então, a solução será:
Sendo que é a solução da equação homogênea, que é a solução de um MHA, ou seja, pode ser do tipo crítico, subcrítico ou supercrítico.
Regime Transiente e Regime Permanente
Mas o que será que acontece com esse sistema após um longo tempo de oscilação?
É o seguinte: Lembra que as equações dos MHA sempre tendiam ao zero, após um longo tempo? Ou seja, sistema com amortecimento tendem a parar uma hora. E na nossa solução geral nós temos que o termo é a solução de um MHA.
Você pode perceber isso notando que as soluções dos MHA sempre tinham um fator assim:
E o limite disso tendendo a infinito dá quanto? Zero! Então, se tendermos a solução geral para um tempo suficientemente grande, um tempo que não precisa ser infinito, vamos perceber que:
Pronto! Ou seja: Após um longo tempo, o sistema vai passar a oscilar apenas em função da força externa, de acordo com a equação acima.
Dizemos que o sistema está no regime transiente quando o tempo é menor que , e permanente quando for maior que . Mas geralmente se diz que o regime permanente acontece após “um longo tempo” ().
Olha aí um gráfico que representa bem isso:
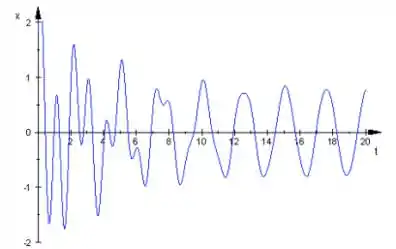
Perceba que antes de o movimento era bem irregular. Isso acontece por causa da soma da equação homogênea com a particular. No entanto, após esse tempo, o sistema passa a oscilar com uma amplitude constante, como um MHS.
É importante saber:
- No regime permanente, o sistema oscila com amplitude constante e dada por
- O regime permanente não depende das condições iniciais () pois a parte que dependia disso era a solução da equação homogênea, que já “morreu” nesse regime. Logo, tudo que ocorrer no regime permanente também não vai depender das condições iniciais.
Ressonância
Ressonância é quando um movimento harmônico forçado atinge o seu máximo de amplitude. Na ausência de amortecimento, a gente já viu que isso ocorre quando a da força externa oscila com a frequência natural do sistema.
No MHA, a primeira coisa que você precisa saber é: ela ocorre no regime permanente.
Como vimos é dada por:
A amplitude máxima pode ser calculada quando
Derivando e resolvendo isso aí, teremos que a amplitude máxima será em:
CUIDADO!! Super comum eles dizerem nas provas que a amplitude máxima é sempre em . Isso não acontece quando a oscilação tem um amortecimento considerável.
Mas se o amortecimento é fraco (), então podemos aproximar a frequência de ressonância para .
Opa! Olha que interessante: Nesse caso, o limite não dá infinito. Isso quer dizer que quando há amortecimento, a ressonância gera uma amplitude máxima na oscilação, porém finita.
Fator de Qualidade ou de mérito
Um tema que costuma cair é o tal fator de qualidade ou fator de mérito. Ele pode ser definido por:
E a relação acima mostra a representação física desse fator. O que podemos tirar disso? Que quanto maior for a dissipação da energia em um ciclo, menor será o fator
É de se esperar, portanto, que seja inversamente proporcional ao E é por isso que pode ser dado por:
E quem é É a chamada largura de banda. Como calcular isso? Bom, quando temos um gráfico :
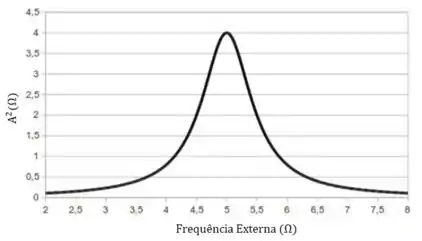
Pra calcular a largura de banda vamos ao eixo em e traçamos uma reta horizontal. A partir do cruzamento dessa reta com o gráfico, descobrimos, rebatendo no eixo , dois valores de . A diferença desses dois valores nos dá a largura de banda:
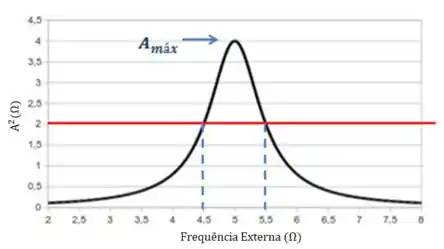
Sacou? No caso desse exemplo:
Observação: As fórmulas acima deduzidas só valem para o caso em que o amortecimento é fraco (
Resumindo
Juntando os conceitos importantes, temos que:
- Se o sistema for amortecido, vai ter um regime transiente, que é o movimento nos primeiros instantes, e um regime permanente, que vai ser um MHS, tendo uma amplitude fixa e frequência da força aplicada. O regime permanente acontece após um longo tempo;
- O regime permanente não depende das condições iniciais, ou seja: e ;
- Amplitude do movimento no regime permanente vai depender de e ;
- Apenas se for pedido, você resolve a EDO não homogênea, do mesmo modo que se faz em Cálculo.
Já sobre ressonância, fique ligado com:
- Não depende das condições iniciais (pois acontece em regime permanente);
- Quanto maior a constante de amortecimento , menor a amplitude de ressonância;
- Para pequenos amortecimentos ou nenhum amortecimento, a ressonância acontece para ;
- Para amortecimentos consideráveis, a ressonância acontece quando
Se liga então! Entendo que estes conceitos não são simples, mas com um pouco de prática eu tenho certeza que você vai ficar craque. VAMO QUE VAMO!
