Exercícios de Intensidade de uma Onda Sonora - Lista de Exercícios Resolvida

Uma fonte pontual de emite ondas sonoras isotropicamente. Supondo que a energia da onda é conservada, determine a intensidade (a) a e (b) a da fonte.

Na figura abaixo, duas fontes sonoras e , separadas por uma distância , estão em fase e emitem ondas isotropicamente com potências e , respectivamente. Um ouvinte se encontra a uma distância da fonte , como mostra a figura. Considere a velocidade do som no ar igual a .

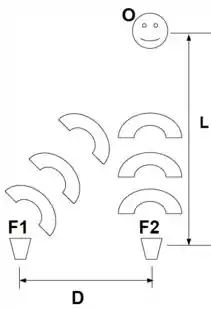
Calcule as intensidade e os níveis sonoros detectados pelo ouvinte , devidos a cada uma das fontes e , separadamente.

O nível sonoro de uma certa fonte sonora é aumentado em . Por que fator é multiplicada (a) a intensidade do som e (b) a amplitude da pressão do ar?

A diferença entre os níveis sonoros de dois sons é . Qual é a razão entre a intensidade maior e a intensidade menor?

Durante uma aula, um professor emite um som com uma potência sonora de . Dado que o limiar de audibilidade corresponde a e admitindo que o som se distribua uniformemente em todas as direções:

1. Calcule o nível sonoro (em ) que um aluno situado a de distância do professor detecta.
2. Qual a distância entre o professor e o aluno, a partir da qual, se o aluno se afastar, ele certamente não ouvirá a voz do professor.
3. Explique o que aconteceria com o valor encontrado no item a) se a frequência da voz do professor duplicasse, mantendo-se a mesma amplitude na posição do aluno. Seja esse novo nível sonoro. Calcule a diferença entre os níveis sonoros.

II-A uma distância de de uma fonte sonora, o nível de um som é de .

c) Determine a que distância a fonte deve estar para que o nível do som caia para .

Duas fontes sonoras ( e), quando ligadas, emitem isotropicamente sons de frequência de no ar. A potência acústica emitida por é igual a Considere um ponto a de e a de .(velocidade do som no ar é igual a ).

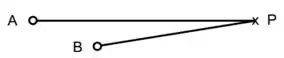
1. A fonte , atuando sozinha, produz em um som de mesma intensidade que a fonte (também atuando sozinha). Calcule a potência acústica de
2. Encontre a diferença de fase das duas ondas que chegam em ( deixei em função de . Diga, justificando, se ocorre interferência construtiva ou destrutiva.
3. Encontre a amplitude dos deslocamentos da onda resultante no ponto.
4. Considere agora que a frequência do som emitido pelas fontes seja . Diga, justificando, que interferência irá ocorrer.
5. Calcule, na situação do item d), a razão entre a intensidade do som em quando e estão ligadas e a intensidade em quando apenas uma fonte está ligada.

II-Considere agora a onda sonora de produzida pelo violino com potência média de ). (Suponha que o som seja emitido isotropicamente).

Dados:

1. Calcule o comprimento de onda, a intensidade e o nível sonoro da onda sonora na posição de um ouvinte a 10 m de distância do violino.
2. Escreva a função , que descreve o deslocamento doselementos de ar na posição desse ouvinte.

O nível sonoro num ponto é abaixo do nível sonoro num ponto a de uma fonte pontual. A distância da fonte ao ponto é:

a)

b)

c)

d) Nenhuma das demais alternativas

e)

Durante uma aula, um professor emite um som com uma potência sonora de . Dado que o limiar de audibilidade corresponde a e admitindo que o som se distribua uniformemente em todas as direções:

1. Calcule o nível sonoro (em ) que um aluno situado a de distância do professor detecta.
2. Qual a distância entre o professor e aluno, a partir da qual, se o aluno se afastar, ele certamente não ouvirá a voz do professor.
3. Explique o que aconteceria com o valor encontrado no item a) se a amplitude da voz do professor aumentasse um fator . Seja esse novo nível sonoro. Calcule a diferença entre os níveis sonoros.

Durante uma aula, um professor emite um som com uma potência sonora de . Dado que o limiar de audibilidade corresponde a e admitindo que o som se distribua uniformemente em todas as direções:

1. Calcule o nível sonoro (em ) que um aluno situado a de distância do professor detecta.
2. Qual a distância entre o professor e o aluno, a partir da qual, se o aluno se afastar, ele certamente não ouvirá a voz do professor.
3. Explique o que aconteceria com o valor encontrado no item a) se a frequência da voz do professor duplicasse, mantendo-se a mesma amplitude na posição do aluno. Seja esse novo nível sonoro. Calcule a diferença entre os níveis sonoros.

Um microfone é colocado no meio da linha que une dois alto-falantes de que podem ser considerados fontes pontuais isotrópicas. Os dois alto-falantes estão separados de uma distância de e emitem uma onda sonora em fase numa frequência de . Despreze as ondas sonoras refletidas na montagem. Dados:

1. Calcule o nível sonoro em medido pelo microfone se apenas um alto-falante estiver ligado.
2. Calcule a intensidade do som em se os dois alto-falantes estiverem ligados.
3. Qual a menor distância que podemos mover o microfone ao longo da linha que une os alto-falantes de modo que a intensidade sonora detectada se torne mínima.

Durante uma aula, um professor emite um som com uma potência sonora de . Dado que o limiar de audibilidade corresponde a e admitindo que o som se distribua uniformemente em todas as direções:

1. Calcule o nível sonoro (em ) que um aluno situado a de distância do professor detecta.
2. Qual a distância entre o professor e aluno, a partir da qual, se o aluno se afastar, ele certamente não ouvirá a voz do professor.
3. Explique o que aconteceria com o valor encontrado no item a) se a amplitude da voz do professor aumentasse um fator . Seja esse novo nível sonoro. Calcule a diferença entre os níveis sonoros.

Um observador A está a 3,0 m de uma lâmpada e um outro observador B está a 12,0 m da mesma lâmpada. Assuma que a luz emitida pela lâmpada se espalha uniformemente e que não sofre nenhuma reflexão ou absorção apreciável. Se o observador B vê a luz com intensidade I , a intensidade observada por A vale

Um médico louco acredita que a calvície pode ser curada esquentando-se o couro cabeludo com ondas sonoras. Seus pacientes sentam-se embaixo de alto-falantes , onde suas cabeças são “banhadas” por 93 dB de ondas sonoras com frequência de 800 Hz. Suponha que uma cabeça calva possa ser considerada um semi-hemisfério de 16 cm de diâmetro. Se uma quantidade de energia sonora de 0,10 J fosse uma dose apropriada para uma seção de terapia, quanto tempo deveria durar uma seção?

1. 42min
2. 30min
3. 15min
4. 12min
5. 21min

Um certo bebê chorando emite som com uma intensidade de . Qual é o nível de intensidade devido a um conjunto de cinco bebês, todos chorando com a mesma intensidade e a mesma distância de você? Você pode negligenciar qualquer absorção, reflexão, ou interferência do som. A menor intensidade detectável é

1. 79 dB
5. 56 dB

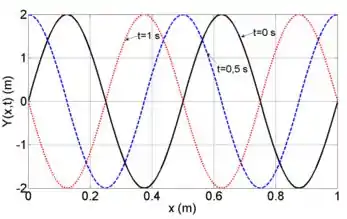
Na figura ao lado, são mostradas três instantes de tempos diferentes ( ) da função que descreve uma onda harmônica propagando-se em uma corda no sentido negativo de

Com base nas informações do gráfico:

1. Calcule o comprimento de onda, o período e a velocidade da onda ( Justifique).
2. Se a tensão na corda é , calcule a densidade linear de massa da corda.
3. Escreva a expressão para o perfil da onda
4. Calcule a velocidade e a aceleração transversais máximas de um elemento da corda.
5. Calcule a intensidade (ou seja, a potência média) da onda na corda.

Um fogo de artifício é detonado muitos metros acima do solo. A uma distância da detonação, o nível de intensidade sonora medida por uma pessoa vale em decibéis. Outra pessoa, a uma distância da detonação, mede um nível de intensidade sonora em decibéis. Supondo que o som se propague isotropicamente, a diferença é igual a:

. Uma fonte sonora pontual emite uma onda esférica que se propaga isotropicamente no ambiente onde existe um detector posicionado a uma distância da fonte. A área desse sensor é de e a potência da fonte é de . Qual a potência no detector?

.

.

.

.

.

Um espectador se encontra a de uma fonte sonora que produz ondas com frequência de e potência de .

a) Determine o nível sonoro percebido pelo espectador e localize (assinale) na figura abaixo o ponto correspondente à onda sonora produzida.

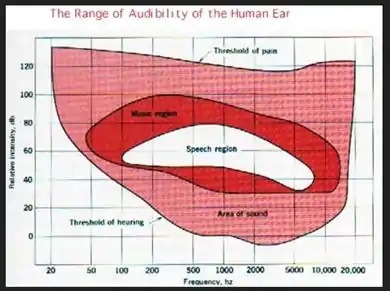
(b) Determine a potência da onda sonora recebida pelo espectador. Considere que o tímpano possui uma área de .

(c) Neste caso, qual a amplitude de vibração dos elementos do meio?

Dados: limiar de audibilidade:

Densidade do ar: .

Na primeira fileira de um show de rock você escutaria a música ser tocada com . O máximo nível de intensidade que um celular emite é . Quantos celulares (no volume máximo) você iria precisar para escutar música no mesmo volume que seria o show de rock?

a) .

b) .

c) .

d) .

e) .

f) .

g) nenhuma das respostas indicadas.

Num estádio de futebol com capacidade para torcedores lotado o microfone de uma emissora de rádio capta um som de de nível de intensidade quando um dos times faz um gol. Supondo que metade dos presentes torcem por este time, o nível de intensidade produzido por cada torcedor ao festejar o gol vale, em média:

(a)

(b)

(c)

(d)

Uma corda de densidade linear de massa m = 50 g cm􀀀1 é esticada sob uma tensão de 720 N. A corda tem de comprimento e, em uma das extremidades, introduzem-se oscilações de frequência com amplitude . Depois de quanto tempo após o início das oscilações, a frente de onda atinge a outra extremidade da corda?

1. 3 s
2. 30 s
3. 0,3 s
4. 0,25 s
5. 2,5 s

O nível de ruído (volume) de som a 4,0 m de uma grande serra elétrica é de 100 dB. A que distância o volume do som será de 80 dB ?

a) 400 m

b) 40 m

c) 5,0 m

d) 3,2 m

e) 0,4 m

Um jato voando a uma altitude de 100 m produz, no solo, um ruído com nível sonoro de 100 dB.Vamos supor que a fonte sonora é uma fonte pontual e isotrópica. Lembre-se que o limite inferior da faixa de audição humana é 10-12 W/m2.

(a) Calcule a potência (em W = J/s) do som produzido pelo jato. Deixe sua resposta em função de .

(b) Qual é a menor altitude que esse jato deve voar para que o ruído no solo não ultrapasse 120 dB, o limiar da dor?

Um estudante de física II foi assistir ao show do Guns and Roses no Rock in Rio. Ele estava se sentindo desconfortável com o barulho e usando um medidor de decibéis, verificou que o nível de intensidade do som atingia o limiar de sensação dolorosa de 120 db a uma distância d1 = 2 m do palco. Com o objetivo de aliviar o desconforto auditivo, o aluno resolveu se afastar a uma distância d2 do palco, até reduzir o nível de intensidade para 100 db. Sabendo que o limiar de audibilidade é , qual deveria ser a distância d2 do aluno em relação ao palco?

(a) d2 = 12 m

(b) d2 = 3 m

(c) d2 = 6 m

(d) Nenhuma da alternativas.

(e) d2 = 10 m

(f) d2 = 20 m

André está localizado a de uma britadeira. O nível de som que Ana ouve é abaixo do nível de som que André escuta. Qual a distância de Ana à britadeira?

De acordo com a legislação brasileira, a intensidade sonora máxima permitida em um turno de 4 horas é . Em uma certa fábrica, 32 máquinas iguais produzem uma intensidade sonora de . Quantas máquinas precisam ser desligadas para que a fábrica esteja de acordo com a legislação?

1. 8;
2. 12;
3. 2;
4. 16;
5. 24;

O limiar de audibilidade de uma onda sonora para uma frequência é dado por e o limiar de sensação dolorosa para a mesma frequência é , onde é a intensidade da onda sonora. Suponha que um alto-falante produza uma onda sonora de de potência com frequência . E que esta onda se propaga de forma esférica e uniforme em todas as direções. Logo, se uma pessoa quer ouvir o alto-falante sem ter sensação de dor deverá estar localizada a qual distância com relação à fonte:

entre e 2.

entre e .

entre e 1000.

entre e 100.

Uma certa onda transversal com amplitude e frequência transfere energia em uma corda a uma taxa média . Se a amplitude e a frequência são dobradas, a nova onda transferirá energia a uma taxa média de:

A intensidade sonora do som a de uma sirene de alerta contra tornados é . A intensidade mais fraca que será ouvida acima do ruído de fundo é . Estime a distância máxima, em quilômetros, a na qual a sirene pode ser ouvida.

A)

B)

C)

D)

E)

Um alto-falante, posicionado sobre um poste alto, emite ondas sonoras igualmente em todas as direções. Se a potência do som na saída do alto-falante é , a que distância dele o nível de intensidade é de ?

1. 5 m
2. 10 m
3. 15 m
4. 20 m
5. 30 m

Na figura abaixo, duas fontes sonoras e , separadas por uma distância , estão em fase e emitem ondas isotropicamente com potências e , respectivamente. Um ouvinte se encontra a uma distância da fonte , como mostra a figura. Considere a velocidade do som no ar igual a .

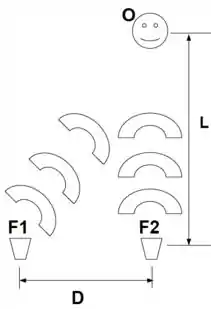
Calcule as intensidade e os níveis sonoros detectados pelo ouvinte , devidos a cada uma das fontes e , separadamente.

Com ambas as fontes ligadas, encontre a mais baixa frequência audível (ou seja, no intervalo de a ) para a qual a intensidade é mínima na posição do ouvinte.

Com ambas as fontes ligadas, encontre a mais baixa frequência audível para a qual a intensidade é máxima na posição do ouvinte.

Um sistema consiste de duas fontes emitindo, em fase, som com a mesma frequência angular dada por . A primeira fonte encontra-se a uma distância do observador, emite com potencia , e chega na posição do observador com amplitude . A fonte se encontra à distância do observador com a potencia vezes maior do que a primeira fonte. Considere que .

Calcule a razão entre as amplitudes e das ondas e, ao chegarem separadamente ao observador.

Calcule a diferença de fase entre as ondas na posição do observador e diga qual o tipo de interferência observado.

Seja uma onda sonora harmônica, com frequência igual a e intensidade . A velocidade do som no ar é e a densidade do ar é .Dado:

1. Calcule o nível sonoro, a amplitude do deslocamento e o valor máximo da variação de pressão.
2. Para essa onda se propagando na direção horizontal, no sentido negativo do eixo x, escreva a função que descreve a onda de deslocamento , especificando todos os valores numéricos, dado que em a camada de ar em está deslocada por , e se movimentando com a velocidade positiva.

Duas fontes pontuais, , estão localizados sobre o eixo à mesma distância da origem do sistema de coordenadas(ver figura). As fontes emitem ondas sonoras cujos deslocamentos são dados por:

é uma constante, são as distâncias de e ao ponto de observação, respectivamente, são medidos em metros e é medido em segundos.

Efetuando-se medidas de nível sonoro sobre pontos localizados sobre o semicírculo mostrado na figura, com centro na origem e raio observou-se que a intensidade é nula em , aumenta até atingir um valor máximo em e volta a ser nulo em

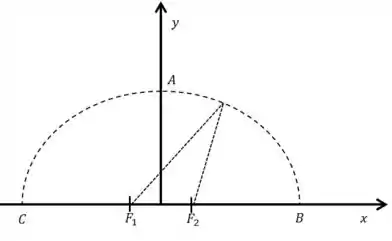
1. Obtenha o número de onda e o comprimento de onda.
2. Obtenha o valor da constante de fase, da onda emitida pela fonte
3. Obtenha a distância entre as duas fontes.
4. Sabendo que a potência sonora emitida por cada fonte é igual a , calcule a intensidade e o nível sonoro(em no ponto caso apenas uma das fontes esteja emitindo. Considere
5. Calcule a intensidade e o nível sonoro em no caso em que as duas fontes estão emitindo simultaneamente.

Dados:

A intensidade de uma onda sonora é 100 vezes a intensidade de outra onda sonora . Com relação ao nível de intensidade, o da onda A em comparação com o da onda B é:

1. maior.
2. maior.
3. maior.
4. maior.
5. maior.

O nível da intensidade sonora a de um alto-falante é (decibéis). Assumindo que a onda produzida pelo alto-falante se propague na forma de onda esférica, a que distância do alto-falante o nível da intensidade cai para ?

Dez trompetistas estão tocando a mesma nota musical com intensidades sonoras iguais. A intensidade sonora medida por um ouvinte na plateia é de 40 decibéis. Suponha que o ouvinte esteja a uma distância grande dos trompetistas, de forma que a diferença de posição entre eles possa ser desprezada. Se nove deles pararem de tocar, a nova intensidade sonora medida será de:

1. 20 decibéis.
2. 40 decibéis.
3. 30 decibéis.
4. 10 decibéis.
5. 4 decibéis.

(Capítulo 15.Problemas – Exercícios 49) Uma onda transversal senoidal com amplitude igual a 2,5 mm e comprimento de onda igual a 1,8 m propaga-se com velocidade de 36,0 m/s da esquerda para a direita ao longo de uma corda esticada horizontal. Considere a origem na extremidade esquerda da corda sem perturbação. No tempo t=0 a extremidade esquerda está sobre a origem e se move de baixo para cima. a) Ache a frequência, a frequência angular e o numero de onda desta onda. b) Qual é a função que descreve a onda? c) Qual é a função para uma partícula na extremidade esquerda da corda? d) Qual é a função para uma partícula situada a 1,35 m à direita da origem? e) Qual é o modulo máximo da velocidade transversal de qualquer partícula da corda? f) Ache o deslocamento transversal e a velocidade transversal de uma partícula situada a 1,35 m à direita da origem para o tempo .

(Capítulo 15.Problemas – Exercícios 50) Uma onda transversal sobre uma corda é dada por a) Ache a amplitude, o período, a frequência, o comprimento de onda e a velocidade de propagação da onda. b) Faça um desenho da corda para os seguintes valores de : e . c) A onda está se deslocando no sentido ou no sentido ? d) A massa por unidade de comprimento da corda é igual a . Ache a tensão e) Ache a potência média transportada por essa onda.

(Cap.16- Ex.18)Qual é o nível da intensidade sonora no ouvido quando a intensidade do som é igual a ? b) Qual é o nível da intensidade sonora nas proximidades de um bate-estacas quando a amplitude de pressão do som é de e a temperatura é igual a ?

(Cap.16 - Ex.21)A boca de um bebê está a de distância do ouvido do pai e a do ouvido da mãe. Qual é a diferença entre o nível de intensidade do som ouvido pelo pai e o nível de intensidade do som ouvido pela mãe?

Dois alto-falantes que emitem som com a mesma frequência, , são colocados ao longo de uma parede e separados por uma distância de 3,00 m. Uma pessoa está de pé a da parede, equidistante dos alto-falantes. Nesta situação ela não ouve som algum. Em seguida a pessoa caminha paralela à parede, ou seja, fica na mesma direção de um dos alto-falantes. Qual a intensidade do som que ela ouve nesta nova localização? Considere a intensidade de um único alto-falante e a velocidade do som no ar igual a .

1. 0

Dois alunos estão conversando em voz baixa em uma biblioteca. A potência do som que deixa a boca de um deles e se espalha uniformemente em todas as direções é 1,2x10-9 W. A que distância (aproximadamente) os alunos devem estar da bibliotecária para que ela mal consiga ouvi-los? O limiar de audição da bibliotecária é 1,0x10-12 W/m2.

a) 9,8 m;

b) 16 m;

c) 23 m;

d) 35 m;

e) 100 m;

Uma determinada linha de produção produz um nível sonoro médio de ruído de , criado por 35 máquinas idênticas. Qual seria o nível sonoro médio de ruído se apenas 4 máquinas estiverem operando?

a)

b) Nenhuma das demais alternativas

c)

d)

e)

Uma pessoa está a uma certa distância de uma fonte sonora que emite ondas isotropicamente. Nesta situação inicial, o indivíduo escuta o som emitido pela fonte com intensidade e um nível sonoro . Em um determinado instante ele se aproxima da fonte, ficando agora a uma distância e fazendo com que seja dez vezes maior que , e o nível sonoro seja . Assinale a alternativa que representa a razão / e a diferenc¸a em , respectivamente.

5 - Um alto-falante num show de música ao ar livre, posicionado no alto do palco, emite ondas sonoras em todas as direções. Se a intensidade sonora a de distância é qual é aproximadamente a potência de saída no alto-falante?

Qual das seguintes alternativas é verdadeira?:

1. A intensidade do som não pode ser negativa, mas o nível de intensidade (em dB) pode ser..
2. Tanto o nível de intensidade (em dB) quanto a intensidade do som não podem ser negativos..
3. O nível do som (em dB) obedece a uma lei do inverso do quadrado da distância, mas a intensidade do som [em energia/(área x tempo)] não
4. Tanto o nível de intensidade (em dB) quanto a intensidade [em energia/(área x tempo)] obedecem a lei do inverso do quadrado das distâncias.
5. Tanto o nível de intensidade em dB quanto a intensidade [em energia/(área x tempo)] do som podem ser negativos.

Uma fonte sonora emite uma onda esférica de modo que um pequeno detector, situado a uma distância da fonte, mede uma intensidade sonora de . Nessa posição, a amplitude da onda de pressão sonora é . Para uma distância do centro de emissão, esse mesmo detector mede uma intensidade e amplitude de pressão , respectivamente iguais a

(a) .

(b) .

(c) .

(d .

(e) .

b) Uma fonte puntiforme produz uma onda sonora esfericamente simétrica com uma potência de .Quanto valem a intensidade e o nível sonoro a uma distância de da fonte? Considere

Se a intensidade sonora em um ponto está abaixo da intensidade sonora em ponto situado a de uma fonte puntiforme. A distância entre o ponto e a fonte é: