Interferência de Ondas
Teoria
Fala Aí! Seja muito bem vindo ao Responde Aí! Bora bater um papo sobre Interferência de Ondas?!
Vamos começar esse papo lembrando da infância! Se você brincava de pular corda quando criança, você já deve ter “sacodido” a corda e criado ondas!
Mas se você sacode a corda de um lado e seu amiguinho sacode de outro, vão ser criado duas ondas que vão se encontrar e quando isso acontece temos uma interferência!
Acontece que interferência é um conceito super importante na física! E hoje a gente vai aprender sobre ele! 😁 Se liga só na imagem abaixo:
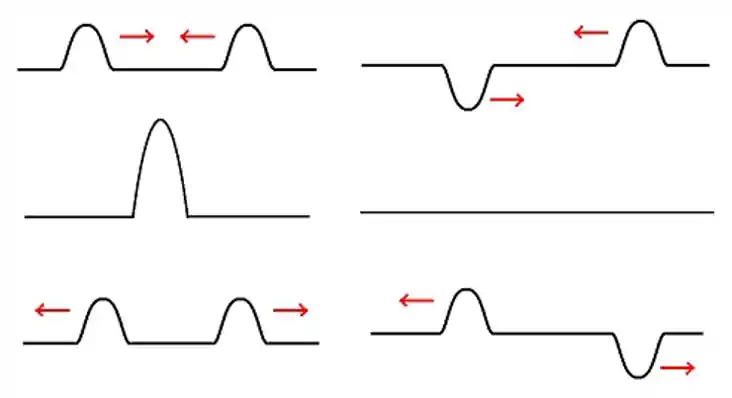
Como a gente pode ver na imagem acima, existem duas possibilidades! As ondas podem se somar, nesse caso a gente cria uma única onda grandona e chamamos esse fenômeno de interferência construtiva ou elas podem ter um efeito de aniquilação, nesse caso temos uma interferência destrutiva!
- Clique aqui para relembrar conceitos importantes de ondas!
Interferência de Ondas: Fórmula
Uma onda pode ser descrita matematicamente usando a seguinte fórmula:
Onde
Então podemos, por exemplo, vamos considerar duas ondas:
Então a onda resultante é dada por:
Logo:
Só somar mesmo! 😉
Interferência Construtiva
A interferência construtiva acontece quando as ondas estão em uma mesma fase
Nesse caso as amplitudes
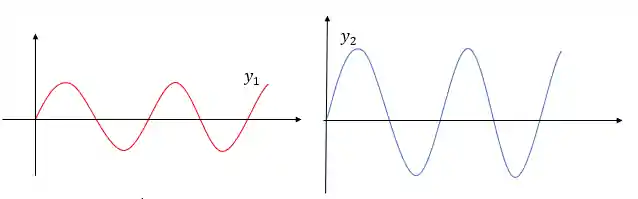
Matematicamente elas são descritas por:
Somando:
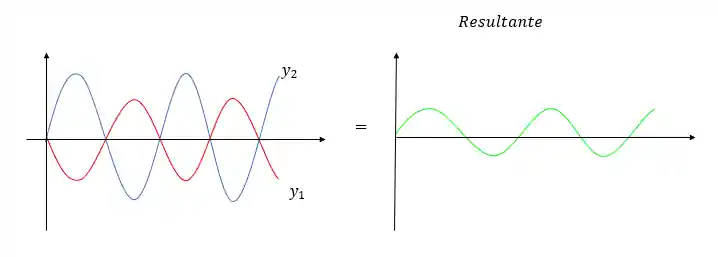
Podemos representar sua soma graficamente:
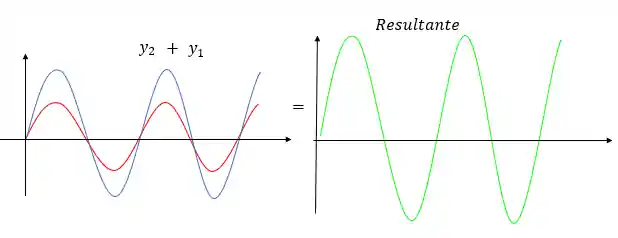
Se medirmos a amplitude da onda vermelha e azul, ela vai dar exatamente a amplitude da onda verde!
Interferência Destrutiva
Se em uma interferência construtiva as amplitudes
Na figura podemos entender melhor como isso funciona, temos um exemplo de duas ondas que sofrem interferência destrutiva:
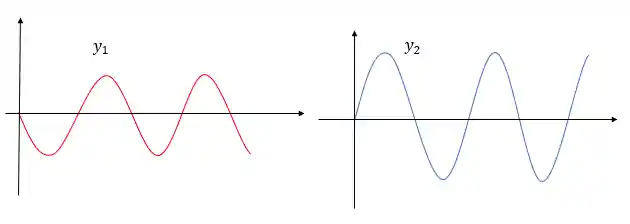
Escrevemos suas equações:
Nesse caso em que há diferença de fase igual a
Logo temos:
Somando:
Graficamente temos:
Acontece exatamente como prevíamos! Em uma interferência desstrutiva as amplitudes se subtraem!
Agora a gente já pode praticar com exercícios!
Interferência de Ondas: Fórmula
Interferência Construtiva
Interferência Destrutiva
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Física 2, Prova2, 2013.2 – Questão 2
Duas ondas harmônicas viajam ao longo da mesma corda. As ondas têm mesmas velocidade e frequência, porém constante de fase e amplitude diferentes. Sabendo que e usando o princípio da superposição, podemos concluir que a amplitude resultante será tal que:
Passo 1
Aqui temos uma interferência entre ondas mecânicas, onde as duas ondas tem constantes de fase diferentes. Não sabemos absolutamente nada dessas fases, então vamos olhar os extremos dessa situação. Qual o pior caso de interferência? A interferência destrutiva, a menor amplitude vai ser
Isso porque
O melhor caso de interferência vai ser a interferência construtiva, a maior amplitude vai ser
Como não sabemos nada das fases a amplitude resultante vai ficar entre um valor e outro
Resposta
Letra D
Exercício Resolvido #2
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 143-31
Duas ondas progressivas iguais, que se propagam no mesmo sentido, estão defasadas de rad. Qual é a amplitude da onda resultante em termos da amplitude comum das duas ondas?
Passo 1
Como elas são iguais e só apresentam defasem de onda, podemos dizer que , e são iguais.
Nesse caso, a amplitude resultante é dada pela fórmula:
onde é a diferença de fase.
Resolvendo:
Resposta
Exercício Resolvido #3
UERJ, Física 2, Lista para P1, Lista de Ondas, Extra - 4
Qual a diferença de fase entre duas ondas progressivas (que de outra forma seriam idênticas) que se movem na mesma direção ao longo de uma corda esticada, que fará com que a onda resultante tenha amplitude 1,5 vezes a da amplitude comum às duas ?
Passo 1
A questão nos diz que as ondas são progressivas e que, se não estivéssemos na situação do problema, elas seriam idênticas.
Logo, podemos deduzir que elas são a mesma onda transladada, ou seja, possuem o mesmo e .
O que isso quer dizer? Quer dizer que podemos usar a equação:
Mas como só estamos interessados na diferença de fase e vamos usar a amplitude resultante, para achá-la, podemos usar apenas:
Onde é a diferença de fase entre as ondas.
(:
Passo 2
Bom, o problema nos diz que a onda resultante tem amplitude 1,5 vezes maior que a onda original. Vamos escrever, então:
Passo 3
Temos quase o que precisamos! Agora basta apelarmos para a trigonometria. Usando a relação:
Logo:
Agora a gente tem que usar uma calculadora científica pra calcular o ! Calculando:
Resposta
Exercício Resolvido #4
UFRJ, Física 2, Prova 2, 2014.1 – Questão 3
Duas ondas harmônicas de mesmas frequências e número de onda interferem. A potência media de cada uma delas é . Qual deve ser a diferença de fase entre elas para que a onda resultante tenha potência média igual a ?
- Não há resposta, pois a potencia média resultante não pode ser maior que a soma das potencias medias individuais.
Passo 1
Queremos saber a diferença de fase entre as ondas.
Sabemos que elas tem o mesmo e o mesmo .
Então as equações das ondas são:
Não sabemos para onda elas se propagam mas isso não vai interferir.
Passo 2
O problema nos diz que as ondas tem o mesmo valor de potência média, separadamente.
Lembrando que potência média é dada por:
Para as duas ondas, temos os mesmos valores de e , pois as ondas tem comprimentos de onda iguais (mesmo valor de ).
Além disso, também é igual, pois as ondas se propagam na mesma corda.
Igualando as potências das ondas, temos:
Logo, as amplitudes também são iguais:
Passo 3
Como temos valores iguais de , e , então a onda resultante é dada por:
E a amplitude resultante é, portanto:
Agora, podemos calcular a potência da onda resultante e comparar com a potência de cada onda sozinha, para descobrir o valor de , que é o que queremos.
Passo 4
Calculando a potência da onda resultante:
Os valores de e são os mesmos que usamos para calcular a potência de cada onda sozinha, pois a onda resultante também tem número de onda e frequência angular .
Além disso, também tem o mesmo valor, pois a corda é a mesma.
Então, só o valor da amplitude muda.
O problema nos diz que:
Logo:
Passo 5
Substituindo fórmulas:
Simplificando:
Tirando a raiz quadrada nos dois lados:
Passo 6
Substituindo :
O ângulo cujo cosseno é é (ou ):
Resposta
Letra D
Exercício Resolvido #5
PUCRIO, Física 2, Prova Final, 2012.2 – Questão 3A
Um pulso numa corda é descrito pela função e um segundo pulso, na mesma corda, é descrito por onde são dados em e em segundos.
Em que direção cada pulso se propaga? Calcule a velocidade de cada pulso.
Determine em que instante os dois pulsos se cancelam totalmente.
Determine em que ponto os pulsos sempre se cancelam.
Passo 1
Para determinar a velocidade e a direção em que o pulso se propaga, podemos manipular a função dos pulsos para achar e então derivamos em relação ao tempo!
Simbora!
Para o pulso , temos:
Para o pulso , temos:
Portanto, temos que o pulso se desloca para a direita, com velocidade e o pulso se desloca para a esquerda com velocidade .
Passo 2
Para que os pulsos se cancelem, temos que , agora é só isolar o tempo para determinar o instante em que isso ocorre!
Passo 3
Para determinar os pontos em que os pulsos sempre se cancelam, precisamos novamente que , mas nesse caso, precisamos determinar . Vamos fazer o mesmo mimimi que fizemos no item anterior!
Show!
Resposta
,