Exercícios de Interferência de Ondas - Lista de Exercícios Resolvida
Questão 1
Qual a diferença de fase entre duas ondas progressivas (que de outra forma seriam idênticas) que se movem na mesma direção ao longo de uma corda esticada, que fará com que a onda resultante tenha amplitude 1,5 vezes a da amplitude comum às duas ?
Ver solução completaQuestão 2
Um pulso numa corda é descrito pela função e um segundo pulso, na mesma corda, é descrito por onde são dados em e em segundos.
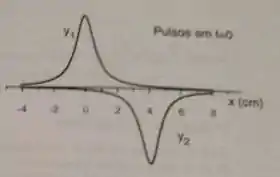
Em que direção cada pulso se propaga? Calcule a velocidade de cada pulso.
Determine em que instante os dois pulsos se cancelam totalmente.
Determine em que ponto os pulsos sempre se cancelam.
Ver solução completaQuestão 3
Duas ondas progressivas iguais, que se propagam no mesmo sentido, estão defasadas de rad. Qual é a amplitude da onda resultante em termos da amplitude comum das duas ondas?
Ver solução completaQuestão 4
Duas ondas harmônicas viajam ao longo da mesma corda. As ondas têm mesmas velocidade e frequência, porém constante de fase e amplitude diferentes. Sabendo que e usando o princípio da superposição, podemos concluir que a amplitude resultante será tal que:
Questão 5
Duas ondas harmônicas de mesmas frequências e número de onda interferem. A potência media de cada uma delas é . Qual deve ser a diferença de fase entre elas para que a onda resultante tenha potência média igual a ?
- Não há resposta, pois a potencia média resultante não pode ser maior que a soma das potencias medias individuais.
Questão 6
Duas ondas harmônicas viajam ao longo da mesma corda. As ondas têm mesmas velocidade e frequência, porém constante de fase e amplitude diferentes. Sabendo que e usando o princípio da superposição, podemos concluir que a amplitude resultante será tal que:
Questão 7
Duas ondas harmônicas se propagam em sentidos opostos na mesma corda com a mesma frequência. É correto afirmar que:
- As duas ondas possuem a mesma velocidade.
- Quando as ondas se encontrarem, haverá interferência construtiva se a diferença de fase entre elas for de
- Como possuem a mesma frequência, a onda que tem maior potência média é aquela que tem maior amplitude.
- Somente a primeira e a terceira alternativas estão corretas
- Todas as alternativas estão corretas.
Questão 8
Duas ondas descritas pelas equações: e , sendo e em , propagam-se em uma corda vibrante. A amplitude da onda resultante é:
Questão 9
Considere duas ondas sonoras, e , de mesma amplitude, , que se propagam da esquerda para a direita seguindo dois diferentes percursos (ver figura). As duas ondas têm o mesmo comprimento de onda, , e estão inicialmente em fase. A onda é refletida por 4 superfícies espaçadas por distâncias , como indica a figura, mas volta a se propagar na direção e no sentido original. No final, e se superpõem produzindo um fenômeno de interferência. Obtenha, em função de , os dois maiores valores de para que a interferência entre e seja:
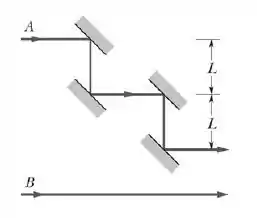
- completamente destrutiva;
- completamente construtiva;
- Obtenha a diferença de fase, , entre e no final dos percursos, em função de e .
- Escreva a amplitude da onda resultante, , em função da amplitude de cada onda e da diferença de fase .
- Calcule, em função de , o maior valor de para que a amplitude resultante seja igual à amplitude de cada onda, separadamente.
Questão 10
Dois pulsos em uma corda se aproximam com uma velocidade de 1m/s como mostrado na figura. Qual é a forma da corda em t = 6 s?
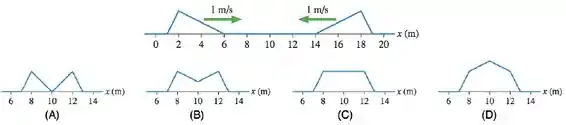
(a) Forma na Figura C.
(b) Forma na Figura A.
(c) Forma na Figura B.
(d) Forma na Figura D
(e) A forma resultante não está ilustrada em nenhuma das figuras.
Ver solução completaQuestão 11
As duas ondas a seguir se propagam em uma corda horizontal:
onde x está em metros e t em segundos.
a) Calcule o padrão de onda resultante na corda. Que tipo de padrão é este? Justifique.
b) Suponha que um antinó do padrão esteja localizado no ponto A. No intervalo de tempo que
este ponto leva para passar da posição de deslocamento máximo para cima para a posição de
deslocamento máximo para baixo, qual é o deslocamento de cada onda ao longo da corda?
Ver solução completaQuestão 12
Duas ondas descritas pelas funções , onde , interferem. Seja a intensidade de uma das ondas. Considere também e como os valores de interferência construtiva máximo e destrutiva mínimo. Em qual dos casos abaixo a intensidade da onda resultante NÃO é igual à ?
(a) , e .
(b.
(c) .
(d) .
(e) .
(f) .
(g) Nenhuma das respostas anteriores.
Ver solução completaQuestão 13
Suponha duas ondas progressivas transversais numa corda sob tensão de densidade linear de massa , dadas por
Com e em metros. A intensidade da onda resultante na corda é:
Questão 14
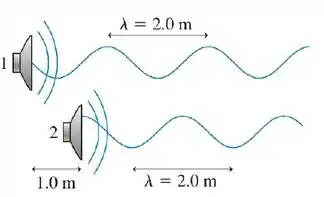
Um alto-falante emite ondas sonoras com intensidade e comprimento de onda . Um segundo alto-falante, idêntico, é colocado à frente do primeiro, mas fora de fase com ele da forma indicada na figura. Sem alterar o volume do som sendo emitido por cada alto-falante, o que se pode fazer para que o som produzido por ambos juntos tenha intensidade ?
A) Não é possível chegar a essa intensidade
B) Atrasar a fase do AF1 de
C) Adiantar a fase do AF1 de
D) Atrasar a fase do AF1 de
E) Adiantar a fase do AF1 de
Ver solução completaQuestão 15
Duas ondas senoidais, viajando em direções opostas, interferem para produzir uma onda estacionária descrita por , onde está em e está em . Qual é a distância (em ) entre os dois primeiros anti-nodos?
A)
B)
C)
D)
E)
Ver solução completaQuestão 16
Um pulso numa corda é descrito pela função e um segundo pulso, na mesma corda, é descrito por onde são dados em e em segundos.
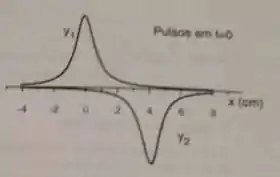
Em que direção cada pulso se propaga? Calcule a velocidade de cada pulso.
Determine em que instante os dois pulsos se cancelam totalmente.
Determine em que ponto os pulsos sempre se cancelam.
Ver solução completaQuestão 17
- Escreva, literalmente, a expressão de uma onda harmônica progressiva unidimensional, propagando-se no sentido positivo do eixo x, em termos da amplitude , da frequência e do comprimento de onda .
- A partir dessa expressão, determine a velocidade máxima com que um elemento do meio se movimenta.
- Suponha que esta onda se superponha a outra de mesma amplitude, mesma frequência e mesmo comprimento de onda, mas se propagando em sentido contrário. Use o Princípio da Superposição e mostre o aparecimento de nós ao calcular a expressão resultante da interferência das duas ondas.
- Se as duas ondas de mesma amplitude , mesma frequência e comprimento de onda se propagam no mesmo sentido, qual deve ser a diferença de fase entre elas para que a amplitude da onda resultante seja
Ver solução completaQuestão 18
Um fio muito longo é feito juntando-se (no ponto B) dois fios com densidades lineares diferentes e . A figura abaixo mostra uma porção do fio, centrada na junção. O fio é esticado sob uma tensão .

- No instante , é produzido um pequeno pulso transversal, localizado no ponto A. Considere as distâncias indicadas na figura. Em que instante de tempo o pulso atinge o ponto C?
- Parte do pulso do item (a) é refletida na junção (ponto B). Determine o instante de tempo em que essa parte do pulso volta ao ponto A?
- Some as duas ondas e obtenha a resultante da sua superposição.
- Caracterize o tipo de interferência resultante (construtiva ou destrutiva, total ou parcial), para cada um dos seguintes valores de e .
Em uma corda muito longa se propagam duas ondas progressivas harmônicas dadas por e .
Questão 19
14 - Em uma corda esticada e fixa nas duas extremidades, são produzidos, a partir do ponto médio entre elas, dois pulsos que se propagam mantendo a forma e a velocidade constantes, conforme a figura abaixo:
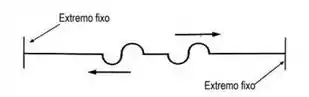
Cada pulso se propaga até ser refletido na respectiva extremidade fixa da corda, e então retorna. Há um determinado instante em que os dois pulsos se superpõem completamente. Nesse momento, a forma resultante na corda é:
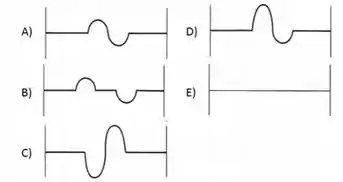
Questão 20
Duas ondas harmônicas de mesmas frequências e número de onda interferem. A potência media de cada uma delas é . Qual deve ser a diferença de fase entre elas para que a onda resultante tenha potência média igual a ?
- Não há resposta, pois a potencia média resultante não pode ser maior que a soma das potencias medias individuais.
Questão 21
Quando duas ondas interferem, a onda resultante apresenta sempre pelo menos uma mudança em relação às ondas componentes. Tal mudança se verifica em relação a(ao):
- Amplitude
- Comprimento de onda
- frequência
- fase
- período
Questão 22
A figura abaixo mostra dois alto-falantes separados por uma distância . Um microfone é posicionado a uma distância em frente a um dos alto-falantes. Um sistema de áudio alimenta os alto-falantes em fase com uma frequência fixa . A velocidade do som no local vale . A frequência é, então, varrida no intervalo audível de a .
- Se , em quantos valores de a intensidade sonora é mínima na posição do microfone?
- Determine o maior valor de , em metros, para o qual ocorre um máximo de intensidade na frequência .