Difração por Duas Fendas Simples
Teoria
Introdução
Se você chegou até aqui já deve ter ouvido falar em interferência por duas fendas pontuais e difração por fenda simples.
Mas e agora, se eu tiver duas fendas maiores que as pontuais, digamos que elas tenham uma largura da mesma ordem de grandeza de uma fenda simples de difração espaçadas numa distância da mesma grandeza da distância das duas fendas pontuais. Ao apontarmos um laser pra essas fendas como será a figura gerada pelo fenômeno?
Desse jeito aqui!
Tá, mas como se formou essa figura diferente que a gente vê na parede?
A figura é a composição dos dois fenômenos já conhecidos só que juntos, esses são:
Interferência por 2 fendas pontuais
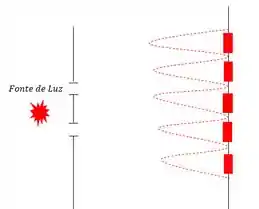
E Difração por fenda simples:
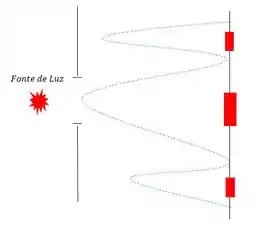
A união dos dois gera a figura de Difração por 2 fendas simples, e o esquema dela em desenho é mais ou menos assim:
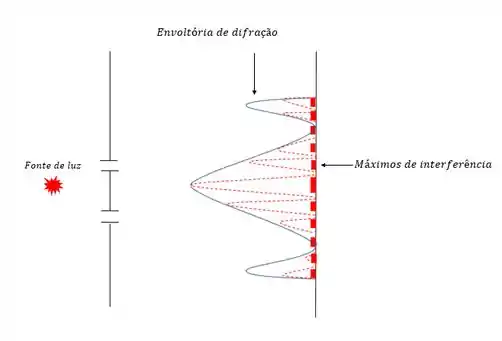
Agora os dois fenômenos agem em conjunto pra criar uma figura nova na parede, essa figura possui o máximo central aumentado como na difração em fenda simples e os máximos secundários pouco espaçados como na interferência em duas fendas.
A figura também possui pontos mínimos de difração e nesses pontos não costuma ter incidência de luz.
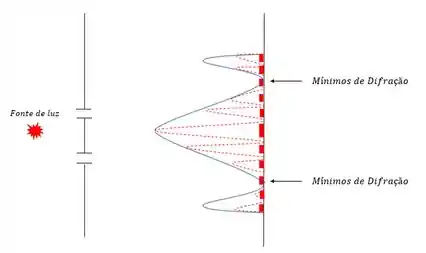
Posição dos máximos e mínimos
Aqui não teremos muitas diferenças os parâmetros continuam os mesmos, se liga na figura:
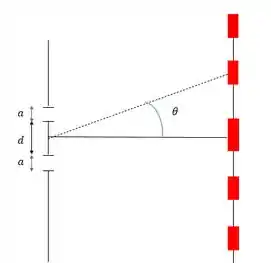
Onde é a largura da fenda, é a distância entre as fendas e é o ângulo a partir do meio do ponto que a gente quer analisar.
Se precisarmos calcular o ângulo de um máximo de interferência faremos como antes:
E de um mínimo de difração ainda é:
Mas agora esses carinhas podem coincidir como na figura que a gente mostrou pro fenômeno da difração em duas fendas, se liga:
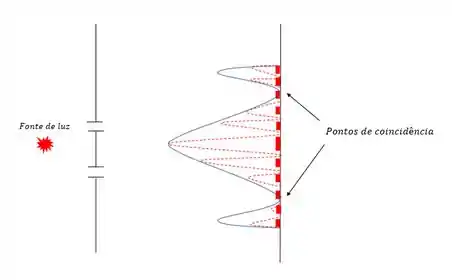
Vamos ver o que acontece? Vamos calcular a razão pra um caso de difração em duas fendas onde o primeiro mínimo de difração coincide com o quinto máximo de interferência e após isso vamos esboçar a figura mostrando quantos máximos de interferência estão compreendidos entre o primeiro e o segundo mínimo de difração.
Para o mínimo de difração temos:
E para o máximo de interferência temos:
E se liga, o comprimento de onda da luz não muda!
Sendo assim a razão é
Enfim:
Mas qual a importância dessa razão? A partir dela a gente sabe a cada quantos máximos vai aparecer um mínimo!
A gente sabe o seguinte, o primeiro mínimo tem um ângulo menor que o segundo pois quanto mais se afasta do centro maior é o ângulo e qualquer máximo compreendido ali terá um ângulo maior que o primeiro mínimo e menor que o maior mínimo se liga na imagem representando um máximo qualquer entre dois mínimos.
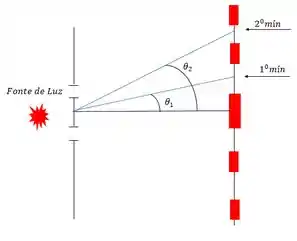
Daí a gente tira que:
E como o seno é aumenta com o ângulo, temos:
E usando a equação da posição dos mínimos de difração temos:
E dos máximos de interferência:
E a relação vai ficar:
Multiplicando tudo por
E enfim:
Mas a gente já encontrou o valor de antes certo? Vamos substituir ele?
Ou seja, entre o primeiro e o segundo mínimo de difração temos:
4 máximos de interferência.
E a figura vai ficar:
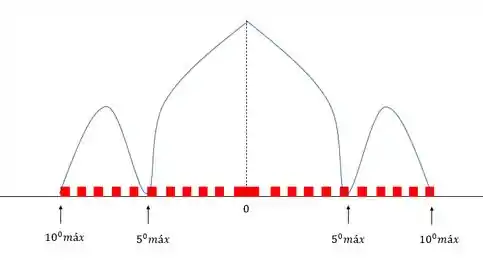
E olha o seguinte o máximo central é o marco 0, ele não conta como máximo nos múltiplos de
Outra coisa interessante é a simetria da figura, ela é idêntica para os dois lados, beleza?
Geralmente os problemas vão te pedir pra encontrar a quantidade de máximos contidos num mínimo e esboçar um gráfico, portanto focamos nisso aqui.
Outra coisa que podem te pedir é a intensidade, vamos ver como é?
Intensidade
Vamos começar olhando graficamente o que acontece, vimos algo parecido na introdução.
O gráfico pra interferência por duas fendas era:
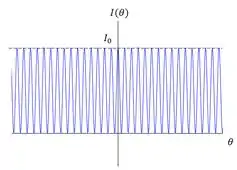
E da figura de difração era desse jeitinho aqui.
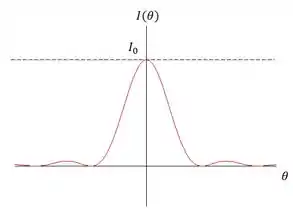
Interferência e difração juntos a gente tem o seguinte gráfico.
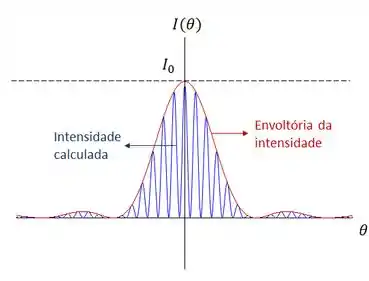
E esse camarada é definido pela equação da intensidade dada por:
Onde cada termo faz predominar um fenômeno, ou seja, cada um é responsável por um fenômeno.
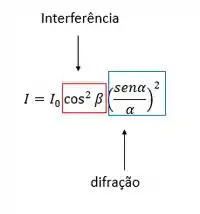
Uma coisa importante, como a equação é um produto de senos e cossenos ao quadrado a intensidade nunca será maior que Isso rola porquê essas funções são limitadas entre -1 e 1, e você pode ver também pelo gráfico.
E quem são os coeficientes que apareceram? Bom o dado em radianos se relaciona com a distância entre as fendas
Um outro jeito de ver esse cara é o seguinte, como:
Lembrando que o é um múltiplo do máximo de interferência aqui!
E o em radianos com a largura da fenda .
Podemos ver esse carinha de outro jeito também:
Lembrando que o é um múltiplo do mínimo de difração aqui!
Pra fixar isso vamos calcular a intensidade de uma luz com para a posição angular de 3. Se a largura das fendas e a distância entre elas é ,sabendo que .
Vamos olhar pra nossa equação da intensidade:
Precisamos de e .
Substituindo na equação em radianos temos:
Substituindo
Então se tivermos um gráfico de não tem mistério só se ligar onde usar as equações em radianos, a dica é deixar os resultados em função de pra ajudar a te lembrar disso.
Posição dos máximos e mínimos
Intensidade
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Física 4, Prova 1, 2012.1, ME1
Considere a interferência da luz de comprimento de onda numa fenda dupla, onde a distância entre o centro das duas fendas é , cada fenda tem uma largura e a figura de interferência encontra-se numa tela a uma distância , tal que .
Sabendo que é o ângulo que define um ponto no anteparo, o primeiro mínimo da difração é dado por igual a:
- Nenhuma das anteriores
Passo 1
Sabemos que os ângulos para os quais encontramos os mínimos de difração são dados por:
Onde:
Passo 2
O problema quer saber o valor do para o primeiro mínimo da difração, isso corresponde ao valor de , logo:
Resposta
Letra (c):
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-38
Duas fendas de largura , separadas por uma distância , são iluminadas por um feixe de luz coerente de comprimento de onda .
Qual é a distância entre as franjas claras de interferência observadas em uma tela situada a uma distância ?
Passo 1
O ângulo entre uma dada franja clara e o máximo central é:
Podemos também encontrar a distância entre essa franja e o máximo central:
Se considerarmos a aproximação de pequenos ângulos, podemos igualar
E obter:
Passo 2
A partir da fórmula anterior, a distância entre duas franjas claras de ordens e seria:
Que para duas franjas consecutivas fica:
Resposta
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-36
Um feixe luminoso monocromático incide perpendicularmente em um sistema de dupla fenda como o da Fig. 35-10. As fendas têm de largura e a distância entre as fendas é .
Quantas franjas claras completas aparecem entre os dois mínimos de primeira ordem da figura de difração?
Passo 1
Vamos fazer esse exercício de duas formas, para treinarmos: A primeira é passo a passo, e a segunda é usando uma dica que diminui muito todo o trabalho (pois ele está todo dentro da dica).
Primeiro nós precisamos saber a distância desses dois mínimos até o centro da figura de difração. Usamos então a condição de mínimos de difração:
Onde é a largura das fendas e é o comprimento de onda da luz. Sendo os dois primeiros mínimos de difração, . Então, o ângulo de cada um é dado por:
Passo 2
Agora, precisamos achar o máximo de interferência com a maior distância do máximo central tal que ela ainda seja menor que a distância dos primeiros mínimos.
Condição de máximos de interferência:
Onde é a distância entre as fendas e é o comprimento de onda da luz. Vamos dizer que o máximo que procuramos é de ordem . Então, seu ângulo é dado por:
Passo 3
Como comentamos antes, o ângulo do máximo de ordem tem que ser menor que o do primeiro mínimo de difração (estamos olhando apenas para o mínimo onde por enquanto)
Logo:
E temos 6 máximos de interferência de um dos lados do máximo central. Se fizermos o mesmo para o outro lado, obteríamos a mesma coisa, porém com . Isso é porque a figura é simétrica.
Logo, temos 12 máximos do lado do máximo central, somando 13 máximos no total (seis de cada lado mais o central).
Passo 4
A forma mais rápida de fazer é pular as etapas de forma consciente.
Todas as etapas que fizemos é o mesmo que procuramos o maior tal que:
Onde é a distância entre as fendas e é a largura das fendas. Substituindo, teríamos de forma direta:
Porém, temos que lembrar que essa desigualdade é para apenas um dos dois lados do máximo central. Então, o número de máximos entre os dois primeiros mínimos de difração seria duas vezes esse valor acrescido de um, representando o próprio máximo central.
Resposta
Entre os dois mínimos de primeira ordem da figura de difração aparecem 13 franjas claras.
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 140-35
Em um experimento de dupla fenda a distância entre as fendas, , é vezes maior que a largura das fendas.
Quantas franjas claras existem na envoltória central de difração?
Passo 1
Para resolver esse problema, temos que trabalhar sempre de forma literal (sem substituir valores, afinal, nós não temos nenhum!).
O maior mínimo que aparece em um dos dois lados do máximo central, dentro da envoltória central de difração é dado por:
Mas o enunciado nos diz que . Substituindo:
Como é um número inteiro, o maior valor possível é:
Passo 2
O número de franjas claras dentro da envoltória central vai ser os máximos de um dos dois lados ( que são máximos) mais os do outro lado (que também são máximos) mais um (o máximo central):
Resposta
Existem 3 franjas claras na envoltória central.
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-40
- Em um experimento de dupla fenda, qual deve ser a razão entre e para que a quarta franja lateral clara seja eliminada?
- Que outras franjas claras também são eliminadas?
Passo 1
Letra a)
Para a quarta franja lateral clara ser eliminada ela precisa coincidir com um mínimo de difração.
A distância angular da quarta franja em relação ao centro da figura é:
A distância angular dos mínimos de difração é:
Se estivermos considerando o primeiro mínimo:
Igualando as distâncias:
Passo 2
Letra b)
As franjas eliminadas serão aquelas que coincidirem com mínimos de difração. Assim:
Substituindo o resultado que encontramos no item anterior
Como , a cada 3 franjas de interferência teremos uma quarta sendo eliminada.
Isso significa as de ordem
Resposta
Letra (a)
Letra (b)
As franjas claras cuja ordem é múltipla de ,
Exercício Resolvido #6
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 136-36.23
Uma figura de interferência é produzida por uma luz de comprimento de onda igual a proveniente de uma fonte distante incidindo sobre duas fendas idênticas paralelas separadas por uma distância (entre seus centros) igual a .
- Se as fendas forem muito estreitas, qual deverá ser a posição do máximo de primeira ordem e do máximo de segunda ordem na experiência de fenda dupla?
- Suponha que a largura de cada fenda seja igual a . Em termos da intensidade no centro do máximo central, qual é a intensidade em cada uma das posições angulares indicadas no item (a)?
Passo 1
O problema nos dá o comprimento de onda e a distância entre as fendas .
Letra (a)
Ok, tem uma informação muito importante “escondida” no enunciado da letra (a).
Quando o problema diz que para considerarmos as fendas muito estreitas, nós passamos a considerá-lo com um problema de interferência.
Logo, a posição dos máximos é dada por
Onde:
;
;
Para :
Para
Passo 2
Letra (b)
A intensidade é dada por:
Onde:
Onde:
Logo:
Como na nossa fórmula pra intensidade tem esses caras divididos por , então fica mais fácil calcular
Para :
;
;
Para :
;
;
Passo 3
Para :
Para
Resposta
Letra (a):
Para
Para
Letra (b):
Para
Para
Exercício Resolvido #7
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-39
- Quantas franjas claras aparecem entre os primeiros mínimos da envoltória de difração à direita e à esquerda do máximo central em uma figura de difração de dupla fenda se , e ?
- Qual é a razão entre as intensidades da terceira franja clara e da franja central?
Passo 1
Letra a)
A distância entre as fendas é e a largura de cada uma é
A franja clara de maior ordem dentro da envoltória central de difração é dada por:
A quantidade de franjas claras que aparecem na envoltória central será:
Passo 2
Letra b)
A razão entre a intensidade de um ponto qualquer e da franja central é:
Onde
Para uma franja clara de interferência:
Nesse caso, sendo a terceira franja:
Substituindo:
Passo 3
Para acharmos a diferença de fase por difração, , precisamos do ângulo da terceira franja. Pelas condições de interferência totalmente construtiva:
Substituindo em :
Na letra (a), vimos que . Logo:
Substituindo na razão de intensidades:
Resposta
Letra (a)
Aparecem franjas na envoltória central.
Letra (b)
Exercício Resolvido #8
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-37
A envoltória central de difração de uma figura de difração por duas fendas contém franjas claras, e os primeiros mínimos de difração eliminam (coincidem com) franjas claras.
Quantas franjas de interferência existem entre o primeiro e o segundo mínimos da envoltória?
Passo 1
O objetivo é descobrirmos quantas franjas de interferência existem entre o primeiro e o segundo mínimo da envoltória de difração. Porém, nós temos poucas informações com as quais trabalhar.
Por isso, vamos tentar aos poucos descobrir do que precisamos.
Para sabermos quantas franjas de interferência existem nessa região, precisamos saber a distância entre o primeiro e o segundo mínimo. Usando as condições de difração, seus ângulos são dados por:
Para ver quantas franjas de interferência estão entre elas, precisamos ver qual a primeira franja nessa região e a última e ver quantas franjas existem entre essas duas ordens.
Passo 2
A primeira franja que procuramos, vai ser a menor ordem tal que seu ângulo é maior que o ângulo do primeiro mínimo de difração. Usando as condições de interferência, seu ângulo será:
A última franja precisa vai ser a de maior ordem tal que seu ângulo seja menor que o ângulo do segundo mínimo de difração.
Fica então mais claro que precisaremos da razão da distância entre as duas fendas com a largura das fendas, .
Passo 3
Agora que sabemos o que procuramos, vamos ver o que temos. Na envoltória central, temos franjas brilhantes, o máximo central e mais 5 de cada lado. Lembrando que:
Sabemos também que o primeiro mínimo de difração coincide com uma franja brilhante. Como a última franja dentro da envoltória é a de ordem , então o primeiro mínimo coincide com a franja seguinte, a de ordem ().
O ângulo dessa franja é dado pela condição de interferência:
Como ela coincide com o primeiro mínimo de difração, podemos igualar os ângulos:
Passo 4
Agora que obtemos o valor de , nós substituímos para achar as franjas que queremos:
Teremos então franjas brilhantes:
Resposta
Entre o primeiro e o segundo mínimo da envoltória de difração temos franjas brilhantes.
Exercício Resolvido #9
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-43
No experimento de interferência de dupla fenda da Fig. 35-10, a largura das fendas é , a distância entre as fendas é , o comprimento de onda é e a tela de observação está a uma distância de .
Seja a intensidade no ponto da tela, situado a uma altura .
- Determine a razão entre e a intensidade no centro da tela.
- Determine a posição de na figura de interferência, especificando o máximo ou o mínimo no qual o ponto se encontra ou o máximo e o mínimo entre os quais o ponto se encontra.
- Determine a posição de na figura de difração, especificando o mínimo no qual o ponto se encontra ou os dois mínimos entre os quais o ponto se encontra.
Passo 1
Letra a)
O nosso primeiro passo é encontrar o ângulo entre o centro da figura e o ponto .
Sabemos que a distância do centro ao ponto é de e a distância das fendas ao anteparo é de .
A tangente do ângulo vai ser a razão desses dois valores:
Passo 2
A razão entre e vai ser:
Onde:
Nessas fórmulas, é a largura das fendas, é a distância entre as fendas e é o comprimento de onda da luz incidente.
Usando o ângulo que encontramos antes:
Juntando todos os resultados:
Passo 3
Letra b)
As condições dos máximos de interferência são:
Enquanto as dos mínimos:
O ângulo do nosso ponto é cujo seno vale:
Em múltiplos de , temos:
Ou seja, está entre o mínimo com (sexto mínimo) e o máximo com (sétimo máximo.
Passo 4
Letra c)
As condições dos mínimos de difração são:
O ângulo do nosso ponto é cujo seno vale:
Em múltiplos de , temos:
Ou seja, está entre o mínimo com (terceiro mínimo) e o mínimo com (quarto mínimo).
Resposta
Letra a)
Letra b)
O ponto está entre o sexto mínimo e o sétimo máximo de interferência.
Letra c)
O ponto está entre o terceiro mínimo e o quarto mínimo de difração.
Exercício Resolvido #10
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-41
Uma luz com um comprimento de onda de passa por um sistema de dupla fenda e produz uma figura de difração cujo gráfico de intensidade em função da posição angular aparece na Fig. 36-47. Determine:
- A largura das fendas
- A distância entre as fendas.
- Mostre que as intensidades máximas indicadas para as franjas de interferência com e estão corretas.
Passo 1
Letra a)
Pelo gráfico, podemos entender que temos um mínimo de difração em pois os máximos próximos estão achatados e com uma distância bem maior que os outros máximos da figura.
Substituindo nas condições de mínimo de difração:
Onde é a largura da fenda, é o comprimento de onda da luz e , pois este é o primeiro mínimo de difração.
Caso sua calculadora só faça o seno de ângulos em radiano, e você não saiba alterar isso, para converter um ângulo de graus em radianos:
Que é uma regra de três já montada. No nosso caso:
Passo 2
Letra b)
As condições de máximo de interferência são:
Pelo gráfico, a terceira franja clara () corresponde a um ângulo de (duas unidades do eixo horizontal são , logo uma unidade são );
Substituindo essas informações e o comprimento de onda:
Passo 3
Letra c)
A fórmula da intensidade é:
Onde:
Para acharmos a intensidade dos máximos correspondentes a e , nós precisamos primeiro achar seus ângulos. No caso , nos já temos. Substituindo os valores:
Pelo gráfico,
Que bate aproximadamente com o gráfico.
Passo 4
Para , o ângulo é dado por:
Substituindo nas equações:
Substituindo na fórmula de intensidade:
Que também aparece estar de acordo com o gráfico.
Resposta
Letra a)
Letra b)
Letra c)
Como demonstrado, as intensidades máximas do gráfico estão de acordo com as calculadas.