Princípios da Interferência
Produzido por Bruno SoaresTeoria
O que é Interferência?
Sabe quando você sopra uma bolinha de sabão, e enxerga várias cores brilhando na superfície dela? Isso é o resultado de um fenômeno que chamamos de interferência.

Princípio da Superposição de Ondas
O fenômeno da interferência é causado pelo Princípio da Superposição de Ondas. Ele diz o seguinte:
“Quando duas ou mais ondas se superpõem, o deslocamento resultante em qualquer ponto em um dado instante pode ser determinado somando-se os deslocamentos instantâneos de cada onda como se ela estivesse sozinha.”
Oi? Calma, que vamos entender melhor.
Vamos supor que duas ondas e se superpõem.
A onda resultante em uma posição e instante é dada por
Sacou?
Interferência para Dois Caminhos Diferentes
Agora imagina duas antenas de rádio, e que por algum motivo emitem ondas em fase (máximos e mínimos sincronizados) uma com a outra. Se as duas emitirem para uma mesma casa (ponto ), essa casa vai conseguir receber o sinal de rádio?
A resposta é menos trivial do que parece! Vamos ver.
Se as ondas emitidas pelas duas antenas percorrem distâncias diferentes, então elas podem sair de fase. Assim, ao se combinarem no ponto , elas vão ter uma diferença de fase, não estando “juntas”.
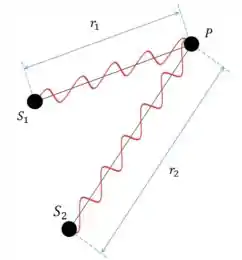
Existem dois casos principais de interferência, nesse caso.
Interferência Construtiva e Destrutiva
Na interferência construtiva, as ondas chegam em fase, com os seus máximos e mínimos sincronizados, e a amplitude resultante vai ser a soma das duas amplitudes.
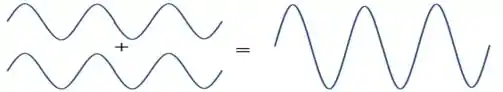
Quando isso vai ocorrer?
Seja a distância entre o ponto e uma fonte de onda e a distância entre o ponto e a fonte de onda . Teremos interferência construtiva quando:
para
Ou seja, ocorre interferência construtiva quando a diferença entre e é igual a um múltiplo inteiro de comprimento de onda .
Quando as ondas de rádio chegarem na casa com uma diferença de fase de meio ciclo (máximos de uma onda sincronizados com mínimos da outra), temos a interferência destrutiva.
Nesse caso, a amplitude resultante será a diferença das amplitudes de cada onda (se forem iguais, então a amplitude resultante é zero!).
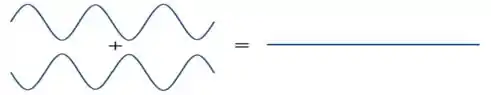
Esse caso ocorre quando a diferença entre e é um múltiplo inteiro do comprimento de onda mais meio comprimento de onda (corresponde a meio ciclo!)
Quando isso acontecer, a pobre casa não vai receber sinal de rádio!!! (Dado que as amplitudes sejam iguais)
Como podemos encontrar a diferença de fase ?
Quando é igual a , as ondas estão em fase. Isso significa que a diferença de fase entre elas é de (uma onda passou pela outra, mas elas se sincronizaram depois). Então, pela regra de três, temos que a relação entre e é dada por
Mas como isso é igual aos casos anteriores???
Bem, quando as duas ondas estão com uma diferença de fase múltipla de (ciclo completo), a interferência é construtiva!
Substituindo esse resultado na equação anterior, teremos:
Onde é um inteiro qualquer.
Quando a diferença é um múltiplo ímpar de (meio ciclo), a interferência vai ser destrutiva!
Substituindo novamente na equação inicial, teremos:
Onde é um inteiro qualquer.
Viu? Os meus resultados que obtivemos antes!
Bora dar uma olhada nos exercícios agora?
Interferência para Dois Caminhos Diferentes
Interferência Construtiva e Destrutiva
Exercícios Resolvidos
Exercício Resolvido #1
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 103-35.5, modificado.
Dois alto-falantes emitindo ondas sonoras idênticas de comprimento de onda igual a em fase uma com a outra e um observador estão posicionados conforme a figura abaixo.
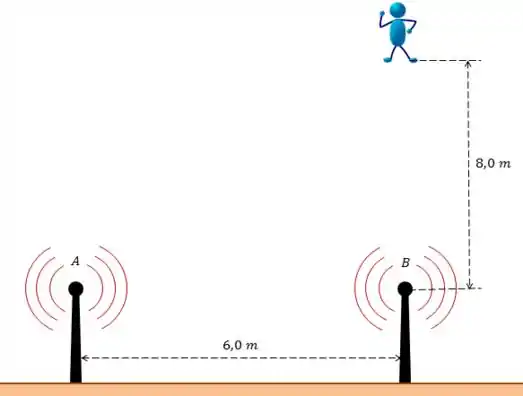
- No local onde está o observador, qual é a diferença entre os caminhos das ondas provenientes dos dois alto-falantes?
- As ondas sonoras irão interferir construtivamente ou destrutivamente no local onde está o observador?
Passo 1
a)
A distância do alto-falante ao observador pode ser achada imaginando-se um triângulo retângulo onde é a hipotenusa. Assim:
A distância do alto-falante ao observador é dada a partir da imagem, de modo que:
Logo:
Passo 2
b)
Dizemos que há interferência construtiva quando:
Da mesma maneira, dizemos que há interferência destrutiva quando:
O problema nos diz que . Logo, os pontos de interferência construtiva serão quando a diferença entre os caminhos for igual a:
Da mesma forma, os pontos de interferência destrutiva serão quando a diferença entre os caminhos for igual a:
Na letra a), vimos que . Logo, o ponto onde o observador está é um ponto de interferência construtiva.
Resposta
a)
b)
O ponto onde o observador está é um ponto de interferência construtiva.
Exercício Resolvido #2
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 103-35.2
Duas antenas de rádio e irradiam em fase. A antena está a à direita da antena .
Considere um ponto ao longo da extensão da linha reta que une as duas antenas, situado a uma distância de à direita da antena .
A frequência e, portanto, o comprimento de onda das ondas emitidas pode variar.
- Qual é o maior comprimento de onda para o qual pode existir interferência destrutiva no ponto ?
- Qual é o maior comprimento de onda para o qual pode haver interferência construtiva no ponto ?
Passo 1
a)
Primeiro, devemos encontrar a diferença entre as distâncias das duas fontes até o ponto Q.
Vamos fazer uma figurinha pra ajudar a visualizar:
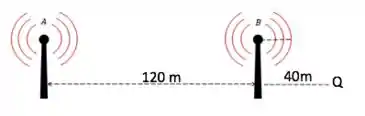
Para a fonte B, temos:
Para a fonte A, temos:
Logo,
Passo 2
Para que a interferência seja destrutiva, é necessário que:
Porém, invertendo a equação, temos:
Ou seja, é o maior possível para o menor possível, que é zero. Aplicando na equação, ficamos com:
Passo 3
Para que a interferência seja construtiva, é necessário que:
Quando temos , podemos inverter a equação e obter
Novamente, vemos que é o maior possível quando é o menor possível. Para , as duas fontes estariam no mesmo ponto, o que sabemos que não é verdade.
Assim, o menor possível é 1, que aplicando na nossa equação fica:
Resposta
a)
Para interferência destrutiva, temos que:
b)
Para interferência construtiva, temos que:
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp-102-23
Na Fig. 35-40, duas fontes pontuais isotrópicas, e , estão sobre o eixo y, separadas por uma distância de , e emitem em fase com um comprimento de onda de .
Um detector de luz é colocado no ponto P, situado sobre o eixo x, a uma distância da origem.
Qual é o maior valor de para o qual a luz detectada é mínima devido a uma interferência destrutiva?
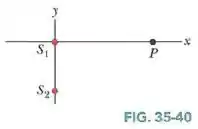
Passo 1
Vamos começar aos poucos, com o que sabemos.
Seja a distância entre e e a distância entre e . Para que a interferência em seja destrutiva, é necessário que:
Assim, a primeira coisa a fazer é encontrar .
Passo 2
Para , vemos que ele está no eixo x, assim como . Logo,
Para , podemos imaginar um triângulo retângulo formado por , e . Isso nos dá, pelo teorema de Pitágoras:
Agora sim, estamos em condição de escrever uma expressão para a diferença dos caminhos de e para .
Passo 3
Com a expressão para a diferença das distâncias, o resto da questão é manipular as expressões pra chegarmos no nosso objetivo. Sabemos que
Vamos passar para o lado direito, e elevar os dois lados ao quadrado.
Vamos expandir a expressão à direita, e dar 3 passos, para chegar numa expressão melhor para nós.
Essa expressão ainda está um pouco feia, mas vai nos ajudar num pequeno raciocínio.
Note que quando aumenta, o numerador diminui, diminuindo . Além disso, o denominador aumenta, também diminuindo . Isso significa que, a medida que aumentar, vai diminuir!
Então, para acharmos o maior tal que a interferência em é destrutiva, precisamos usar o menor possível, que é zero.
Passo 4
Com o que discutimos, vamos então substituir na nossa expressão.
Por fim, uma última mudança, pra equação ficar a melhor possível pra gente.
Mas o problema nos disse que . Com isso, finalmente, atingimos nossa resposta:
Resposta
O maior valor de possível para que a interferência seja destrutiva é .