Método dos Fasores
Teoria
O que são fasores?
São vetores de faz de conta! Entendeu? “Fasores”....
Ok, piadas ruins a parte, nós temos agora que resolver um problema deixado em aberto.
Quando eu tenho ondas eletromagnéticas interferindo entre si em um ponto qualquer, qual vai ser o campo elétrico resultante? Vamos discutir o caso para duas ondas.
Imagina que eu tenho duas ondas eletromagnéticas com campos elétricos senoidais e de mesma amplitude , mesma frequência e mesma direção. A diferença de fase deles no ponto é .
Matematicamente, podemos escrever os campos como:
A interferência entre eles vai ser a soma desses dois. Você pode somar na mão mas tá com uma cara que vai dar um trabalhão pra expandir esse cosseno aí....
Existe uma forma mais visual de fazer isso, por um tipo de “vetor” que representa as oscilações das ondas, chamados Fasores.
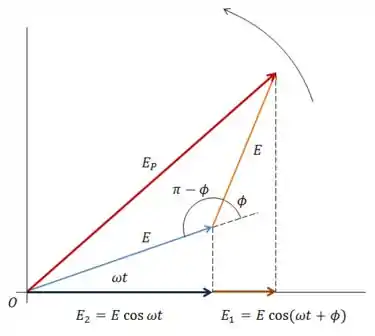
O ângulo entre o fasor e o representa a fase da onda (o que fica dentro do coseno), enquanto a projeção do fasor no representa a onda em si.
Como uma soma vetorial é a soma de suas componentes, podemos calcular o campo elétrico resultante de dois fasores pelo gráfico, usando a lei dos cosenos
Agora, usando a identidade trigonométrica:
Dá pra simplificar o resultado
Como a intensidade é proporcional ao quadrado da amplitude do campo elétrico, a intensidade resultante vai ser:
Que era a nossa fórmula pra intensidade de fenda dupla!!!
Pra que mais serve?
Você pode somar vários tipos de ondas malucas assim!
Vamos supor que você tenha os seguintes campos
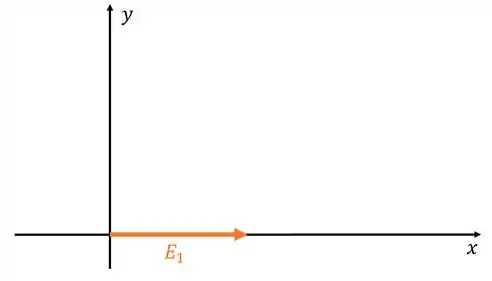
Como é que seria a soma desses 3 caras? Na prática você pode pensar no momento em que , pra colocar o primeiro campo sobre o eixo .
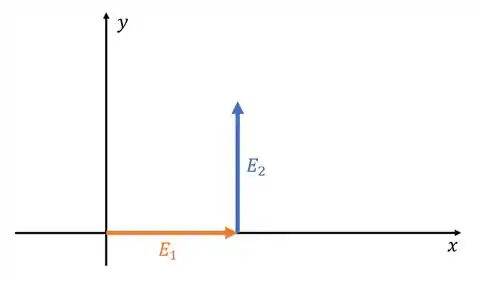
E o segundo? Olhando pra fórmula fórmula ele tem um ângulo de com o eixo horizontal, ou seja, ele é vertical.
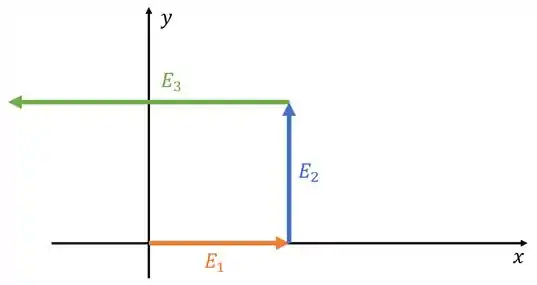
E o terceiro? Esse faz um ângulo com a horizontal então, ao contrário do , ele tem que apontar para a esquerda. Também tem que prestar atenção que o módulo dele é o dobro do primeiro hein!
Agora só tem que fazer o resultante que nem a gente faz com vetores mesmo!
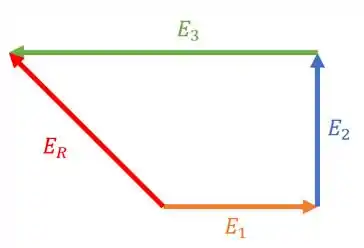
Agora é só aplicar a magia da geometria pra calcular a intensidade desse e o ângulo que ele faz com a horizontal.
Traçando uma reta pontilhada vertical do começo de até o meio de , nós formamos um triângulo retângulo que tem como hipotenusa .
O cateto vertical desse triângulo tem o mesmo tamanho de , que é , e o lado vertical é metade do tamanho de , que é também!
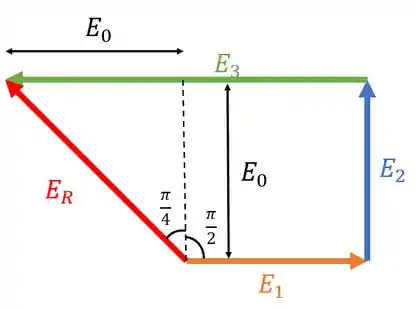
Assim temos que
Já o ângulo entre a reta pontilhada e é
De forma que a fase (o ângulo em e a horizontal) será
Assim a nossa soma maluca vai ficar
E aí a gente volta com o .
Um caso especial é quando temos uma figura fechada como essa aqui
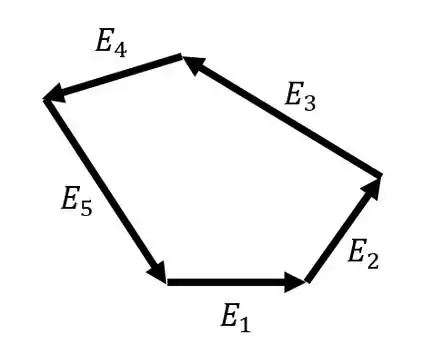
No caso de uma figura fechada o campo resultante é nulo.
É como se esses campos fossem deslocamentos e no final de todos deslocamentos voltássemos pro ponto de partida de forma que o deslocamento resultante é nulo!
E aí? Feshow? Vamos praticar? o/
Pra que mais serve?
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Física 4, Prova 1, 2011.2
Duas fontes emitem campos elétricos na mesma direção e de mesma frequência com amplitudes iguais a .
Os campos interferem num ponto em que a diferença de fase entre eles é de .
A amplitude resultante será (dica: use fasor):
Passo 1
O problema nos dá a amplitude dos campos elétricos e a diferença de fase entre eles , e nos pede para calcular o campo elétrico resultante no ponto .
De acordo com os dados, o diagrama de fasores pode ser dado por:
Passo 2
Analisando o diagrama de fasores, a amplitude do campo elétrico resultante é calculado a partir da Lei dos Cossenos para o triângulo formado:
Onde:
;
;
;
Logo:
Resposta
Letra (e):
Exercício Resolvido #2
UFRJ, Física 4, Prova 1, 2015.1
Cinco ondas eletromagnéticas senoidais de mesma amplitude incidem num detector, cujos campos elétricos, neste ponto, são dados por:
A amplitude do campo elétrico resultante no detector é dada por:
- Nenhuma das anteriores
Passo 1
Vamos começar esboçando o diagrama de fasores, em , pra essa situação:
Passo 2
Como o campo elétrico resultante está na vertical, temos apenas que calcular as componentes verticais de cada campo elétrico.
Assim, o campo elétrico resultante será:
A resposta certa é a letra .
Resposta
Exercício Resolvido #3
PUC-Rio, Física 4, Prova 1, 2013.2
Obtenha o campo elétrico resultante da soma vetorial dos seguintes campos elétricos em uma interferência produzida por um dispositivo com três fendas:
Passo 1
Queremos calcular a seguinte soma vetorial:
Para calcular a soma vetorial, uma boa dica é desenhar os vetores em um diagrama, lembrando que estamos somando os três vetores dados.
Para facilitar, iremos fazer a seguinte substituição:
Desse modo, podemos montar o seguinte diagrama:
Explicitamente, queremos somar:
Podemos ver no diagrama que estão especificados os vetores dados, assim como o vetor soma .
O campo elétrico resultante da soma será:
Para determinar precisamos recorrer a algumas relações matemáticas, se liga!
Passo 2
Pelo desenho, podemos ver a seguinte relação:
Veja que estamos analisando a soma das componentes de todos os vetores na direção do vetor .
Analisando a outra componente, temos:
Passo 3
Agora que temos o valor das duas componentes, podemos determinar utilizando o teorema de Pitágoras, dá uma olhada!
Substituindo os valores, temos:
Passo 4
Precisamos agora determinar o ângulo , para isso, basta fazer:
O campo elétrico resultante é:
Resposta