Espelhos Esféricos
Teoria
Como o nome sugere, os espelhos esféricos têm a forma de uma pequena seção da superfície de uma esfera.
Tipos de espelhos esféricos
Existem dois tipos de espelhos esféricos: os côncavos e os convexos. Para entender um pouco melhor cada tipo de espelho, vamos fazer uma comparação com o espelho plano.
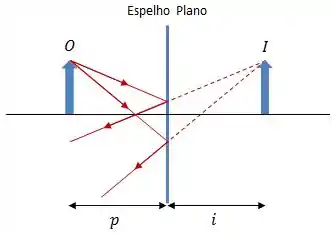
Vamos considerar que tudo o que está na frente do espelho se encontra à esquerda, do mesmo lado que está o objeto. E tudo o que está atrás do espelho se encontra à direita, lado oposto ao do objeto.
Nas imagens abaixo é o centro de curvatura, é o centro do espelho, é o objeto, é a distância do objeto ao centro do espelho, é a imagem e é a distância da imagem ao centro do espelho.
Côncavo: centro de curvatura na frente do espelho, campo de visão diminui.
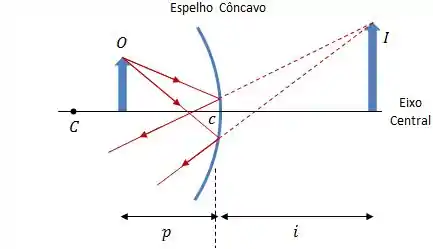
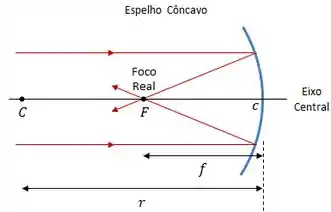
Em um espelho côncavo, os raios que incidem paralelamente ao eixo central convergem para um mesmo ponto, chamado ponto focal , ou foco. Da mesma forma, os raios que incidem sobre o foco, refletem paralelamente ao eixo central.
Como o foco está no mesmo lado do objeto, nós o chamamos de foco real.
Convexo: centro de curvatura atrás do espelho, campo de visão aumenta.
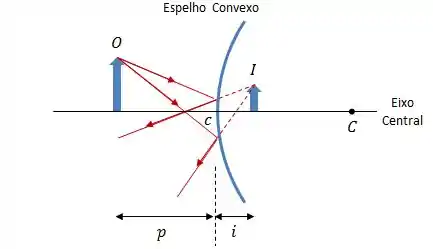
Em um espelho convexo, os raios paralelos divergem a partir do foco virtual (que se encontra no lado oposto ao do objeto). Se liga:
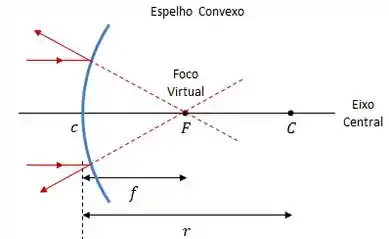
Imagens formadas por espelhos esféricos
Existem algumas relações bastante importantes que precisamos saber e que serão necessárias pra resolvermos boa parte dos problemas.
A distância entre o foco e o centro do espelho é chamada distância focal . E a distância entre o centro de curvatura e o centro do espelho é chamada de raio de curvatura .
A distância focal e o raio de curvatura estão diretamente relacionados por:
Além disso, existe uma importante relação direta entre a distância focal , a distância entre o objeto e o centro do espelho e a distância entre a imagem e o centro do espelho:
Seja a altura de um objeto e seja a altura da imagem correspondente, a ampliação lateral é definida por:
O valor é positivo quando a imagem possui a mesma orientação do objeto, e é negativo quando a imagem possui orientação oposta ao do objeto.
A ampliação lateral também pode ser calculada a partir da equação:
Um último detalhe importante sobre as imagens formadas por espelhos esféricos: imagens reais se formam do mesmo lado do espelho em que se encontra o objeto e imagens virtuais do lado oposto.
Análise Gráfica de Espelhos Esféricos
Muitos problemas de espelhos esféricos acabam envolvendo a análise de gráficos. Assim, vamos mostrar dois dos casos mais comuns e como resolvê-los.
Gráfico
A situação aqui é a seguinte: começamos a deslocar o objeto a partir do centro de um espelho esférico até uma distância do espelho. Durante o movimento, a distância entre a imagem e o centro do espelho é medida.
O gráfico abaixo mostra o valor de em função da distância do objeto até uma distância , onde .
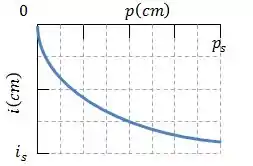
A pergunta é: qual é a distância da imagem quando o objeto está a uma distância do espelho?
Como , não podemos simplesmente tirar o valor de do gráfico porque ele não estará lá (parece um bom motivo, né?).
Como o gráfico mostra, se mudarmos a distância , mudaremos a distância . Então vamos precisar de um parâmetro que seja constante.
Esse parâmetro é a distância focal . Assim, nesse tipo de problema, um bom primeiro passo costuma ser calcular o valor de .
Para isso, precisamos buscar no gráfico um ponto da curva e usar os respectivos valores de e para calcular .
Na hora de escolher esse ponto, procure prestar atenção para escolher um ponto em que os valores sejam fáceis de pegar, como o exemplo abaixo:
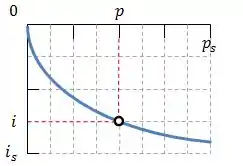
Escolhidos os valores de e , basta calcular a distância focal através da expressão:
Agora que finalmente calculamos , basta usar o valor de dado pelo problema e calcular o valor de através da expressão:
Gráfico
A situação agora é muito parecida com a anterior. Assim como antes, começamos a deslocar o objeto a partir do centro de um espelho esférico até uma distância do espelho.
Durante o movimento, a ampliação lateral é medida. O gráfico abaixo mostra o valor de em função da distância do objeto até uma distância , onde .
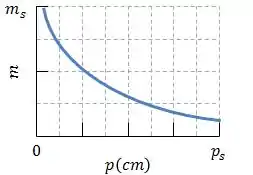
A pergunta é: qual é a ampliação lateral do objeto quando este se encontra a uma distância do espelho?
Assim, precisamos encontrar o valor de para calcular o valor de . Para isso, um bom começo é calcular a distância focal do espelho, dada por:
Devemos escolher um ponto no gráfico, e a distância será dada por:
Agora que temos os valores de e correspondentes, podemos calcular a distância focal .
Depois, através do valor de e, calcular o valor de correspondente:
Finalmente, agora com todos os dados necessários, o valor da ampliação lateral correspondente à distância será dada por:
Obs.: O importante aqui não é decorar o passo-a-passo, mas entender a lógica para resolver esse tipo de problema.
Identificando o Espelho Esférico
E se tiver uma questão pedindo pra você dizer se um espelho é côncavo ou convexo através de gráficos e informações? Calma, vamos ver aqui o que podemos diferenciar...
Espelho Côncavo
Como vimos antes, o espelho côncavo possui as seguintes características:
- Centro de curvatura na frente do espelho;
- Campo de visão diminui;
- A distância e tamanho da imagem aumentam em relação ao espelho plano.
O gráfico de em função de tem mais ou menos essa cara:
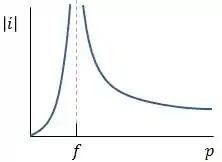
Vemos que o gráfico possui uma descontinuidade, para entender melhor o que acontece, vamos explicando cada trecho separadamente:
- : Quando o objeto está entre o centro do espelho e o foco, a imagem formada é virtual (ou seja, é formada no lado do espelho oposto ao do objeto);
- : Quando o objeto está sobre o foco, não é formada nenhuma imagem pelo espelho. Isso explica o porquê da descontinuidade;
- : A partir dessa distância, a imagem formada pelo espelho é real, e o valor de diminui gradativamente, como mostra o gráfico.
Assim, a descontinuidade aparece no momento em que a imagem muda de plano, deixando de se formar no plano virtual, para se formar no plano real.
Espelho Convexo
O espelho convexo possui as seguintes características:
- Centro de curvatura atrás do espelho;
- Campo de visão aumenta;
- A distância e tamanho da imagem diminuem em relação ao espelho plano.
O gráfico abaixo relaciona em função de :
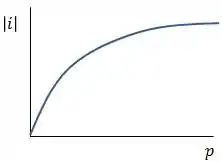
Nesse gráfico não temos nenhuma descontinuidade, como no caso do espelho côncavo. Isso ocorre porque todas as imagens formadas pelo espelho convexo são virtuais.
Assim, já conseguimos diferenciar os espelhos =)
Vamos praticar?
Imagens formadas por espelhos esféricos
Análise Gráfica de Espelhos Esféricos
Identificando o Espelho Esférico
Exercícios Resolvidos
Exercício Resolvido #1
Randall D. Knight, Física Uma Abordagem Estratégica – Volume 2, 2a ed. Porto Alegre: Bookman, 2009, pp 735
Um objeto encontra-se à frente de um espelho convexo cuja distância focal é . A imagem é direita ou invertida? Real ou virtual? Menor ou maior?
Passo 1
Nesse exercício, nos foi dado a distância do objeto ao espelho convexo:
E também nos foi dado a distância focal:
(Esse valor negativo, indica que o foco é virtual o que é uma característica do espelho convexo.)
Agora, para encontrarmos a posição da imagem usaremos a fórmula:
E utilizaremos a fórmula do aumento linear para identificar se a imagem é maior ou menor e se estará invertida ou não:
Passo 2
Encontrando a posição da imagem:
Aqui você não precisa se preocupar em colocar os valores de para não, tá? No final, você vai encontrar um valor também! Continuando...
Opa, portanto a imagem será virtual (pois tem o valor negativo) e está a uma distância de cm do espelho.
Passo 3
Agora vamos para o aumento linear:
Com isso, definimos que é uma imagem menor, na verdade, ela será 40% do tamanho original.
Além disso, como o aumento deu positivo, indica que a imagem estará na mesma direção que o objeto.
Portanto, a imagem é virtual, direita e menor.
Mas pensa no espelho convexo! Tem um bizu importante sobre ele!
Toda imagem formada por um espelho convexo é virtual, direita e menor.
Resposta
A imagem é virtual, direita e menor.
Exercício Resolvido #2
Randall D. Knight, Física Uma Abordagem Estratégica – Volume 2, 2a ed. Porto Alegre: Bookman, 2009, pp 735
Um objeto encontra-se à frente de um espelho côncavo cuja distância focal é . Use o traçado de raio para localizar a imagem. A imagem é direita ou invertida?
Passo 1
Partiu fazer rascunho porque ninguém aqui vai decorar cada imagem proveniente de cada posição, certo?
Então vamos lá:
Temos, então, uma imagem virtual, direita e maior.
Mas e a sua posição?!
Passo 2
Resposta
A imagem é virtual, direita e maior, localizada atrás do espelho.
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 65
Um objeto é colocado no centro de um espelho esférico e deslocado ao longo do eixo central até uma distância de do espelho.
Durante o movimento a distância entre o espelho e a imagem do objeto é medida. A figura abaixo mostra o valor de em função da distância do objeto até uma distância .
Qual é a distância da imagem quando o objeto está a do espelho?
Passo 1
A singularidade no gráfico é típica de espelho côncavos, ela ocorre quando a imagem deixa de ser real para se tornar virtual. Isso ocorre quando:
Assim, do próprio gráfico já podemos concluir que, sendo :
Passo 2
Para descobrir a distância da imagem, basta usar a equação:
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 71
Um objeto é colocado no centro de um espelho esférico e deslocado ao longo do eixo central até uma distância de do espelho.
Durante o movimento a distância entre o espelho e a imagem do objeto é medida. A figura abaixo mostra o valor de em função da distância do objeto até uma distância .
Qual é a distância da imagem quando o objeto está a do espelho?
Passo 1
Vamos começar calculando a distância focal da lente, para isso vamos escolher no gráfico um ponto do qual possamos retirar facilmente os dados necessários.
No gráfico, podemos usar o ponto em que e .
Logo:
Substituindo os valores, teremos:
Passo 2
Agora podemos calcular a distância do problema.
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 74
Uma xícara de chá é posicionada sobre o eixo central de um espelho esférico. A ampliação lateral da xícara é e a distância entre o espelho e o ponto focal é .
Qual é a distância entre o espelho e a imagem?
A distância focal é positiva ou negativa?
A imagem é real ou virtual?
Passo 1
Qual é a distância entre o espelho e a imagem?
A partir da ampliação lateral podemos encontrar uma relação entre e .
Como
Passo 2
Como temos o valor de , podemos usar a seguinte relação:
Onde , logo:
Como não sabemos o sinal de , podemos apenas calcular o módulo de , dado por:
Passo 3
A distância focal é positiva ou negativa?
No Passo 1 vimos que:
No entanto, necessariamente precisa ser positivo. Isso significa que o valor de é negativo, ou seja, a imagem é virtual.
Voltando agora para a equação que encontramos no Passo 2, temos:
Assim, como é negativo, a distância focal também é negativa.
Passo 4
A imagem é real ou virtual?
Como já falamos antes, o valor de é negativo, logo, a imagem é virtual.
Resposta
A distância focal é negativa.
A imagem é virtual.
Exercício Resolvido #6
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 63
Um pinguim caminha ao longo do eixo central de um espelho côncavo, do ponto focal até uma grande distância do espelho.
Qual é o movimento correspondente da imagem?
A altura da imagem aumenta continuamente, diminui continuamente, ou varia de uma forma mais complicada?
Passo 1
Qual é o movimento correspondente da imagem?
A imagem formada por um espelho côncavo par é real com a orientação invertida em relação ao objeto. Assim, o pinguim vai se afastar, mas na imagem ele vai estar de cabeça para baixo.
Passo 2
A altura da imagem aumenta continuamente, diminui continuamente, ou varia de uma forma mais complicada?
Quanto mais longe do foco, menor a imagem vai se tornando. No entanto, a distância entre o espelho e a imagem obedece à equação:
Onde:
corresponde à altura da imagem e corresponde à altura do objeto.
Como e são constantes, podemos ver que, conforme aumenta, a altura da imagem diminui segundo a equação acima, de forma mais complicada.
Resposta
O pinguim vai se afastar, mas a imagem terá orientação invertida em relação ao pinguim original.
A altura da imagem diminui, mas de forma mais complicada.
Exercício Resolvido #7
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 65
Um objeto é deslocado ao longo do eixo central de um espelho esférico enquanto a ampliação lateral é medida. A figura abaixo mostra o valor de em função da distância do objeto no intervalor de e .
Qual é a ampliação do objeto quando está a do espelho?
Passo 1
Vamos começar calculando a distância focal da lente.
Para isso, um bom ponto no gráfico para começarmos a trabalhar é o ponto cujas coordenadas são:
Logo:
Passo 2
A distância focal será:
Substituindo os valores, teremos:
Passo 3
A distância da nova imagem será:
Passo 4
A ampliação lateral desejada será dada por:
Resposta
Exercício Resolvido #8
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 66
A figura abaixo mostra a ampliação lateral de um objeto em função da distância do objeto em relação a um espelho esférico quando o objeto é deslocado ao longo do eixo central do espelho.
A escala do eixo horizontal é definida por . Qual é a ampliação do objeto quando este se encontra a do espelho?
Passo 1
Vamos começar calculando a distância focal da lente.
Para isso, um bom ponto no gráfico para começarmos a trabalhar é o ponto cujas coordenadas são:
Logo:
Passo 2
A distância focal será:
Substituindo os valores, teremos:
Passo 3
A distância quando será:
Passo 4
A ampliação lateral desejada será dada por:
Resposta
Exercício Resolvido #9
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 65
Quando um tiranossauro persegue um jipe no filme Jurassic Park vemos uma imagem refletida na lateral do jipe, onde está escrito (o que, dadas as circunstâncias, pode ser considerado uma piada de humor negro): “Os objetos vistos neste espelho estão mais próximos do que parecem”. O espelho é convexo ou côncavo?
Passo 1
Quando o aviso diz que os objetos estão mais próximos do que parecem, significa que a imagem formada pelo espelho é menor. Além disso, esse tipo de espelho tem o objetivo de aumentar o campo de visão.
Baseado nisso, pode-se afirmar que o espelho é convexo.
Resposta
O espelho é convexo.
Exercício Resolvido #10
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 64
Um objeto é colocado no centro de um espelho côncavo e deslocado ao longo do eixo central até uma distância de do espelho. Durante o movimento, a distância entre o espelho e a imagem do objeto é medida. O processo é repetido para um espelho convexo e um espelho plano.
A figura abaixo mostra o resultado em função da distância do objeto. Determine a correspondência entre as curvas e o tipo de espelho. ( a curva 1 tem duas partes)
Passo 1
A curva 1 apresenta uma singularidade, isso é típico dos espelhos côncavos, e ocorre quando a imagem deixa de ser real e se torna virtual.
A curva 2 não apresenta descontinuidades e a curva não é linear. Portanto, a curva é referente a um espelho convexo.
A curva 3 é linear, típico de espelhos planos, uma vez que .
Resposta
Curva 1: Espelho côncavo;
Curva 2: Espelho convexo;
Curva 3: Espelho plano.
Exercício Resolvido #11
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 63-64
Na figura abaixo o boneco está em frente de um espelho esférico montado no interior da região tracejada; o eixo central do espelho está indicado na figura.
Os quatro bonecos a mostram a localização e a orientação de possíveis imagens produzidas pelo espelho.
(As alturas e distâncias dos bonecos não foram desenhadas em escala.)
Quais dos bonecos não podem representas imagens?
Das imagens possíveis, determine as que não podem ser produzidas por um espelho côncavo; as que não podem ser reproduzidas por um espelho convexo; as que são virtuais; as que envolvem uma ampliação negativa.
Passo 1
Quais dos bonecos não podem representar as imagens?
O espelho côncavo gera imagens reais e com orientação invertida quando e gera imagens virtuais com a mesma orientação do objeto para .
O espelho convexo gera imagens virtuais e com a mesma orientação do objeto.
O boneco é uma imagem real (já que está do mesmo lado do objeto) e com a mesma orientação que o objeto.
O boneco é uma imagem real e com a orientação invertida em relação ao objeto.
O boneco é uma imagem virtual (já que está do lado oposto ao do objeto) e com a mesma orientação do objeto.
O boneco é uma imagem virtual e com a orientação invertida em relação ao objeto.
Assim, a partir das características de cada imagem, pode-se afirmar que os bonecos e não podem representar as imagens.
Passo 2
Das imagens possíveis, determine as que não podem ser produzidas por um espelho côncavo.
Conforme dito anteriormente, o espelho côncavo gera imagens reais e com orientação invertida quando e gera imagens virtuais com a mesma orientação do objeto para .
As imagens e podem ser formadas por um espelho côncavo. Logo, nenhuma das imagens possíveis não pode ser produzida por um espelho côncavo.
Passo 3
Das imagens possíveis, determine as que não podem ser reproduzidas por um espelho convexo.
Um espelho convexo gera uma imagem virtual e com a mesma orientação que o objeto.
Assim, a imagem não pode ser formada por um espelho convexo.
Passo 4
Das imagens possíveis, determine as que são virtuais.
Imagens virtuais são aquelas formadas no lado oposto ao do objeto.
A imagem é virtual.
Passo 5
Das imagens possíveis, determine as que envolvem uma ampliação negativa.
As imagens virtuais possuem ampliação negativa.
A imagem possui ampliação negativa.
Resposta
Os bonecos e não podem representar as imagens.
Nenhuma das imagens possíveis não pode ser produzida por um espelho côncavo.
A imagem não pode ser formada por um espelho convexo.
A imagem é virtual.
A imagem possui ampliação negativa.
Exercício Resolvido #12
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 66
Um ponto luminoso está se movendo com velocidade em direção a um espelho esférico de raio de curvatura , ao longo do eixo central do espelho. Mostre que a imagem do ponto está se movendo com uma velocidade dada por
Onde é a distância instantânea entre o ponto luminoso e o espelho.
Suponha agora que o espelho é côncavo, com um raio de curvatura , e que .
Determine a velocidade da imagem para (bem mais longe do espelho que o ponto focal), (ligeiramente mais longe do espelho que o ponto focal) e (muito perto do espelho).
Passo 1
Mostre que a imagem do ponto está se movendo com uma velocidade dada por
Onde é a distância instantânea entre o ponto luminoso e o espelho.
A seguinte equação relaciona as distâncias , e :
Reorganizando essa equação, encontramos o seguinte:
Onde:
Substituindo na equação acima, teremos:
Passo 2
A velocidade da imagem será dada por:
Onde .
Agora vamos no braço, passo a passo da conta!
Considerando a velocidade do objeto como positiva, como a imagem se move no sentido oposto, será dado por:
Passo 3
Determine a velocidade da imagem para (bem mais longe do espelho que o ponto focal).
Sabendo que e , temos que:
Passo 4
Determine a velocidade da imagem para (ligeiramente mais longe do espelho que o ponto focal).
Sabendo que e , temos que:
Passo 5
Determine a velocidade da imagem para (muito perto do espelho).
Sabendo que e , temos que:
Resposta