Lentes Delgadas
Produzido por Ludovic BeghinTeoria
Uma lente é um corpo transparente limitado por duas superfícies refratoras com um eixo central em comum.
Quando a lente está imersa no ar, a luz é refratada ao penetrar na lente, atravessa a lente, é refratada uma segunda vez e volta a se propagar no ar.
As duas refrações podem mudar a direção dos raios.
Vamos trabalhar com dois tipos de lentes:
- Lente Convergente: raios incidem paralelos ao eixo central se aproximam do eixo.
- Lente Divergente: raios se afastam do eixo central.
A imagem abaixo exemplifica como os raios se comportam para cada tipo de lente:
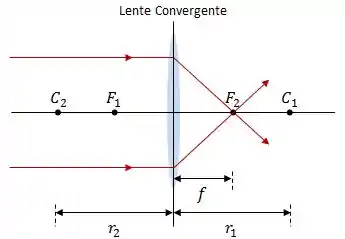
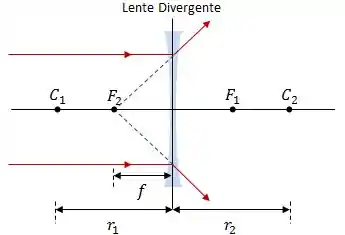
Um detalhe muito importante relacionado à distância focal é o seguinte:
- Se a lente for convergente, então o valor de será positivo;
- Se a lente for divergente, então o valor de será negativo;
Para os nossos problemas, vamos considerar apenas lentes delgadas: lentes nas quais a distância do objeto , a distância da imagem e os raios de curvatura e das superfícies da lente são muito maiores que a sua espessura.
Para uma lente delgada com índice de refração imersa no ar, a distância focal é dada por:
Além disso, uma relação que usamos muito em espelhos esféricos e que continua sendo válida para lentes é dada por:
Imagens formadas por lentes delgadas
Agora que já sabemos como cada lente se comporta, precisamos entender como as imagens são produzidas.
Para isso, temos que ter em mente apenas três regras:
- Um raio que incide paralelo ao eixo central, após ser refratado, passa pelo ponto focal ;
- Um raio que incide sobre o ponto focal , após ser refratado, se torna paralelo ao eixo central;
- Um raio que passa pelo centro da lente emerge da lente sem sofrer mudanças na sua direção;
O ponto de encontro de dois ou mais raios é o ponto onde a imagem é formada, vamos aplicar as nossas regras nos dois tipos de lentes:
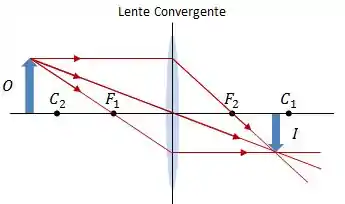
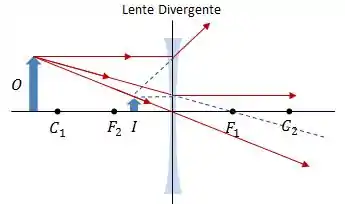
As lentes convergentes formam imagens da seguinte forma:
- : Imagem real e com a orientação invertida em relação ao objeto;
- : A lente não forma imagens;
- : Imagem virtual e com a mesma orientação do objeto;
Já as lentes divergentes formam imagens virtuais e com a mesma orientação que o objeto.
Análise Gráfica de Lentes Delgadas
O que vamos fazer agora é mostrar dois dos casos mais comuns de análise de gráficos de lentes delgadas e como resolvê-los.
A primeira situação é a seguinte. Imagine que você desloca um objeto até uma distância da lente. Você vai ter o seguinte gráfico:
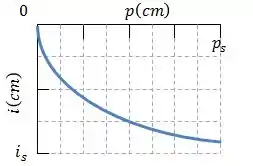
Qual é a distância da imagem quando o objeto está a uma distância da lente?
Como , não podemos simplesmente tirar o valor de do gráfico porque ele não estará lá. Vamos precisar de um parâmetro que seja constante: a distância focal .
Assim, nesse tipo de problema, um bom primeiro passo costuma ser calcular o valor de . Precisamos buscar no gráfico um ponto da curva e usar os valores de e para calculá-la.
Depois que finalmente calculamos , basta usar o valor de dado pelo problema e calcular o valor de através da expressão:
ATENÇÃO! Assim como o espelho côncavo, a lente convergente não forma imagem quando o objeto se encontra sobre o foco . Assim, o gráfico desse tipo de lente tem essa cara:
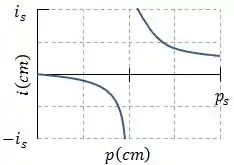
O gráfico pode parecer um pouco estranho, mas ele já nos ajuda bastante. Ele apresenta uma descontinuidade, e o ponto em que essa descontinuidade ocorre é justamente a distância focal , já que quando o objeto está sobre ele a imagem não é formada. Nesse caso, podemos tirar do próprio gráfico a distância focal , e economizamos os cálculos.
Agora vamos analisar o gráfico que mostra a variação da amplitude lateral em função da distancia do objeto.
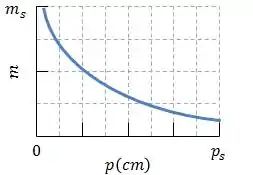
Qual é a ampliação lateral do objeto quando este se encontra a uma distância da lente?
A ideia aqui é bem parecida: precisamos encontrar o valor de para calcular o valor de . Para isso, um bom começo é calcular a distância focal da lente. Escolhe-se dois pontos do gráfico, , e a distância será dada por:
Agora que temos os valores de e correspondentes, podemos calcular a distância focal . O próximo passo é utilizar a mesma expressão e, através do valor de , calcular o valor de correspondente:
Finalmente, agora com todos os dados necessários, pode-se calcular o valor da ampliação lateral .
Identificando a Lente
Já sabemos as principais características de cada lente... mas e se ele te dá o gráfico de em função de e pede pra você dizer qual lente é? Calma, vamos ver direitinho.
Para a lente convergente, esse gráfico tem essa cara:
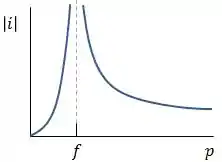
Vemos que o gráfico possui uma descontinuidade, para entender melhor o que acontece, vamos explicando cada trecho separadamente:
- : Quando o objeto está entre o centro da lente e o foco, a imagem formada é virtual (ou seja, é formada no mesmo lado da lente que objeto);
- : Quando o objeto está sobre o foco, não é formada nenhuma imagem pela lente. Isso explica o porquê da descontinuidade;
- : A partir dessa distância, a imagem formada pela lente é real, e o valor de diminui gradativamente, como mostra o gráfico.
Assim, a descontinuidade aparece no momento em que a imagem muda de plano, deixando de se formar no plano virtual, para se formar no plano real.
Já para a lente divergente, ele tem essa cara aqui ó:
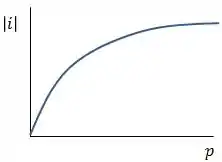
Nesse gráfico não temos nenhuma descontinuidade, como no caso da lente convergente, isso ocorre porque todas as imagens formadas pela lente divergente são virtuais.
Show? Agora já sabemos como diferenciar as lentes através do gráfico de em função de .
Combinação de Lentes
Agora vamos complicar um pouco mais as coisas... e se tivermos um objeto diante de um conjunto de duas ou mais lentes cujos eixos centrais se coincidem e queremos localizar a imagem final do sistema?
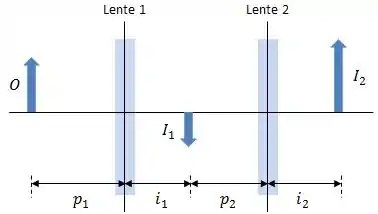
Obs.: As posições, tamanho e orientações do objeto e das imagens e são completamente arbitrárias. Além disso, as lentes foram representadas por retângulos porque há diversas combinações possíveis.
A estratégia que temos que usar pra resolver esse problema é a seguinte:
Vamos chamar de a distância entre o objeto e a lente 1. A partir daí, calculamos a distância entre a imagem e a lente traçando os raios, ou usando a seguinte equação:
Depois vamos ignorar a presença da lente 1 e vamos passar a considerar a imagem como o objeto da lente 2.
Importante! Se o novo objeto (imagem ) estiver à direita da lente 2, a distância será considerada negativa. Agora, se o novo objeto (imagem ) estiver à esquerda da lente 2, a distância será considerada positiva.
Finalmente, basta calcular a distância traçando os raios, ou utilizando a seguinte equação:
Esse método pode ser aplicado a um sistema com lentes! :O
Ah, só mais uma coisa! A ampliação lateral total em um sistema formado por lentes delgadas é dada por:
Onde é ampliação lateral da lente .
Show? Ufa! Vamos pros exercícios agora =)
Imagens formadas por lentes delgadas
Análise Gráfica de Lentes Delgadas
Identificando a Lente
Combinação de Lentes
Exercícios Resolvidos
Exercício Resolvido #1
Randall D. Knight, Física Uma Abordagem Estratégica – Volume 2, 2a ed. Porto Alegre: Bookman, 2009, pp 735
Um objeto encontra-se à frente de uma lente convergente cuja distância focal é . Use o método de traçado de raios para determinar a localização da imagem. Ela é direita ou invertida?
Passo 1
Vamos pegar régua, papel e lápis e vamos rascunhar!
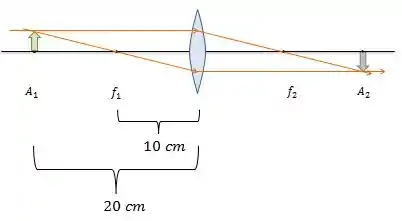
Mas para sermos mais rápidos, basta perceber que a posição do objeto equivale a duas vezes o valor de seu foco, o que indica que está no antiprincipal da lente. E o que sabemos? Se o objeto está no antiprincipal , a imagem é do mesmo tamanho e está no antiprincipal .
Resposta
Invertida, localizada a do espelho, para a direita.
Exercício Resolvido #2
Elaboração própria
Um objeto encontra-se à frente de uma lente divergente cuja distância focal é . Determine a localização da imagem, caracterize esta imagem e defina o aumento linear da mesma.
Passo 1
Vamos lá, mole para nós!
Temos o foco e a distância , logo, podemos achar a distância .
Passo 2
Opa, temos negativo, então nossa imagem é virtual e direita. Baste sabermos se é maior ou menor. Vamos para o aumento linear.
Logo, virtual, direita e menor.
Resposta
Imagem virtual, direita e menor.
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 64
A figura abaixo mostra quatro lentes delgadas, todas feitas do mesmo material, com lados que são planos ou têm um raio de curvatura de em módulo.

Sem fazer nenhum cálculo, coloque as lentes na ordem do módulo da distância focal, começando pela maior.
Passo 1
Nas lentes e , somente as superfícies esféricas “contribuem” para a distância focal. Assim, as duas possuem distâncias focais iguais, mas com sinais contrários. Mas como estamos analisando o módulo da distância focal, teremos:
Passo 2
Na lente , como o raio de curvatura de cada superfície está para um lado, a distância focal resultante será menor que das lentes e , logo:
Passo 3
Na lente , como os raios das superfícies esféricas estão para o mesmo lado, o valor da distância focal dessa lente será maior que as anteriores, logo:
Resposta
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 67
Um objeto é colocado no centro de uma lente delgada e deslocado ao longo do eixo central até uma distância de da lente. Durante o movimento a distância entre a lente e a imagem do objeto é medida. A figura abaixo mostra o resultado em função da distância do objeto até .
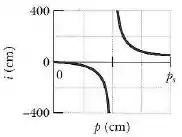
Determine a distância da imagem para
Passo 1
A singularidade no gráfico é típica de lentes convergentes, ela ocorre quando a imagem deixa de ser real para se tornar virtual. Isso ocorre quando:
Assim, do próprio gráfico já podemos concluir que:
Passo 2
Para descobrir a distância da imagem, basta usar a equação:
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 67-68
Um objeto é colocado no centro de uma lente delgada e deslocado ao longo do eixo central até uma distância de da lente. Durante o movimento a distância entre a lente e a imagem do objeto é medida. A figura abaixo mostra o resultado em função da distância do objeto até .
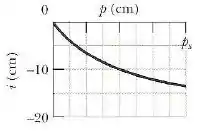
Determine a distância da imagem para
Passo 1
Vamos começar calculando a distância focal da lente, para isso vamos escolher no gráfico um ponto do qual possamos retirar facilmente os dados necessários.
No gráfico, podemos usar o ponto em que e .
Logo:
Substituindo os valores, teremos:
Passo 2
Agora podemos calcular a distância do problema.
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #6
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 67-68
Um objeto é colocado no centro de uma lente delgada e deslocado ao longo do eixo central. Durante o movimento a ampliação lateral é medida. A figura abaixo mostra o resultado em função da distância do objeto até .
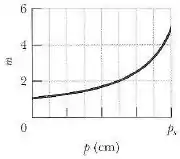
Determine a ampliação lateral do objeto para .
Passo 1
Vamos começar calculando a distância focal da lente.
Para isso, um bom ponto no gráfico para começarmos a trabalhar é o ponto cujas coordenadas são:
Logo:
Passo 2
A distância focal será:
Substituindo os valores, teremos:
Passo 3
A distância da nova imagem será:
Passo 4
A ampliação lateral desejada será dada por:
Resposta
Exercício Resolvido #7
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 68
Na figura abaixo uma imagem real invertida de um objeto é formada por uma certa lente (que não aparece na figura); a distância entre o objeto e a imagem, medida ao longo do eixo central da lente, é .

A imagem tem metade do tamanho do objeto.
Que tipo de lente é capaz de produzir a imagem?
A que distância do objeto deve ser colocada a lente?
Qual deve ser a distância focal da lente?
Passo 1
Que tipo de lente é capaz de produzir a imagem?
Se trata de uma lente convergente, visto que somente esse tipo de lente é capaz de formar imagens reais.
Passo 2
A que distância do objeto deve ser colocada a lente?
A relação entre as distâncias e , onde é a distância entre o objeto e a imagem, é dada por:
Como o enunciado disse, a imagem tem a metade do tamanho do objeto, isso significa que:
Logo:
Substituindo na primeira equação, teremos:
Onde , logo:
Passo 3
Qual deve ser a distância focal da lente?
A distância focal pode ser calculada através da seguinte equação:
Onde:
Logo:
Resposta
Se trata de uma lente convergente.
Exercício Resolvido #8
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 72
Duas lentes delgadas de distâncias focais e estão em contato. Mostre que são equivalente a uma única lente delgada com uma distância focal .
Passo 1
O nosso arranjo possui duas lentes, onde as duas estão em contato. Assim como vimos na teoria, vamos pensar em cada lente separadamente, beleza?
Pensando na Lente 1, as distâncias e e a distância focal estão relacionadas por:
O macete aqui é posicionar o objeto a uma distância praticamente infinita da Lente 1.
Oi?! Como assim?!
Calma... se liga no que acontece se nós considerarmos :
Ou seja, a imagem será formada sobre o foco.
Passo 2
Agora vamos para a Lente 2, aplicando a mesma fórmula que usamos anteriormente:
Agora, a imagem formada pela Lente 1 será o objeto da Lente 2. Dessa forma, podemos dizer que:
Se for positivo, a imagem formada pela Lente 1 está atrás da Lente 2 e será negativo, ou seja, o objeto para a Lente 2 é virtual.
Se for negativo, a imagem formada pela Lente 1 está à frente da Lente 2 e será positivo, ou seja, o objeto para a Lente 2 é real.
Aplicando o que encontramos no Passo 1, teremos:
Passo 3
Agora vamos pensar no conjunto das duas lentes em contato como uma lente só. Assim, as distâncias , e serão relacionadas por:
Assim como vimos no Passo 1, estamos colocando o objeto a uma distância infinita do sistema. Logo, para , teremos:
No entanto, a distância para o qual a imagem será formada se trata da distância da Lente 2. Portanto:
Passo 4
Agora que já encontramos uma relação para e , podemos aplica-las na seguinte equação:
Onde:
Logo:
Agora é só reorganizar esse cara:
Finalmente:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #9
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 71
Na figura abaixo uma caixa se encontra sobre o eixo central da lente convergente delgada de algum ponto à esquerda da lente.
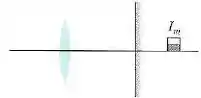
A imagem da caixa, produzida pelo espelho plano, que está à direita do espelho. A distância entre a lente e o espelho é , e a distância focal da lente é .
Qual é a distância entre a caixa e a lente?
A luz refletida pelo espelho atravessa novamente a lente e produz uma imagem final da caixa.
Qual é a distância entre a lente e a imagem final?
Passo 1
Qual é a distância entre a caixa e a lente?
Se a imagem da caixa está a à direita do espelho plano, então a imagem gerada pela lente está a à esquerda do espelho plano.
Logo, a imagem formada pela lente estará a uma distância da lente, dada por:
Sabendo que a distância focal da lente é , o objeto estará a uma distância da lente, dada por:
Substituindo os valores, teremos:
Passo 2
Qual é a distância entre a lente e a imagem final?
Agora a imagem formada pelo espelho plano funciona com objeto. Dessa maneira, a distância entre o novo objeto e a lente será:
Assim, a distância entre a lente e a imagem final será:
Onde . Logo:
Resposta
Exercício Resolvido #10
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 64
Na figura abaixo o boneco está em frente de uma lente delgada, simétrica, montada no interior da região tracejada; o eixo central do espelho está indicado na figura.
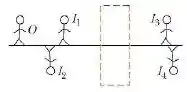
Os quatro bonecos a mostram a localização e a orientação de possíveis imagens produzidas pela lente.
(As alturas e distâncias dos bonecos não foram desenhadas em escala.)
Quais dos bonecos não podem representar as imagens?
Das imagens possíveis, determine as que não podem ser produzidas por uma lente convergente; as que não podem ser reproduzidas por uma lente divergente; as que são virtuais; as que envolvem uma ampliação negativa.
Passo 1
Quais dos bonecos não podem representar as imagens?
O boneco é uma imagem virtual (já que está do mesmo lado do objeto) e com a mesma orientação que o objeto. Essa imagem pode ser formada por lentes divergentes e convergentes.
O boneco é uma imagem virtual e com a orientação invertida em relação ao objeto. No entanto, nenhum tipo de lente pode gerar essa imagem.
O boneco é uma imagem real (já que está do lado oposto ao do objeto) e com a mesma orientação do objeto. No entanto, nenhum tipo de lente pode gerar essa imagem.
O boneco é uma imagem real e com a orientação invertida em relação ao objeto. Essa imagem é típica de lentes convergentes.
Assim, os bonecos e não podem representar as imagens.
Passo 2
Das imagens possíveis, determine as que não podem ser produzidas por uma lente convergente.
Uma lente convergente gera uma imagem real e invertida se , ou uma imagem virtual e com a mesma orientação se .
As imagens e podem ser formadas por lentes convergentes. Logo, nenhuma das imagens possíveis não pode ser produzida por uma lente convergente.
Passo 3
Das imagens possíveis, determine as que não podem ser reproduzidas por uma lente divergente.
Uma lente divergente gera uma imagem virtual e com a mesma orientação que o objeto.
Assim, a imagem não pode ser formada por uma lente divergente.
Passo 4
Das imagens possíveis, determine as que são virtuais.
Imagens virtuais são aquelas formadas no mesmo lado que o objeto.
A imagem é virtual.
Passo 5
Das imagens possíveis, determine as que envolvem uma ampliação negativa.
As imagens virtuais possuem ampliação negativa.
A imagem possui ampliação negativa.
Resposta
Os bonecos e não podem representar as imagens.
Nenhuma das imagens possíveis não pode ser produzida por uma lente convergente.
A imagem pode ser formada por uma lente divergente.
A imagem é virtual.
A imagem possui ampliação negativa.
Exercício Resolvido #11
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 72
Você fabrica as lentes que aparecem na figura abaixo a partir de discos planos de vidro usando uma máquina capaz de produzir um raio de curvatura de ou .

Em uma lente na qual é necessário apenas um raio de curvatura, você escolhe o raio de . Em seguida, usa as lentes, uma por uma, para formar uma imagem do sol.
Determine a distância focal e o tipo de imagem (real ou virtual) da lente biconvexa 1; e o tipo de imagem da lente plano-convexa 2; e o tipo de imagem da lente côncavo-convexa 3; e o tipo de imagem da lente bicôncava 4; e o tipo de imagem da lente plano-côncava 5; e o tipo de imagem da lente convexo-côncava 6.
Passo 1
Determine a distância focal da lente biconvexa 1;
A distância focal é dada por:
Obs.: Consideraremos os raios de curvatura das superfícies voltadas para a direita como positivo, e das superfícies voltadas para a esquerda como negativos. Além disso, as superfícies planas possuem raio de curvatura infinito.
Para a lente 1, teremos:
Passo 2
Determine o tipo de imagem (real ou virtual) da lente biconvexa 1;
Como , a imagem é real.
Passo 3
Determine a distância focal da lente plano-convexa 2;
Para a lente 2, teremos:
Passo 4
Determine o tipo de imagem (real ou virtual) da lente plano-convexa 2;
Como , a imagem é real.
Passo 5
Determine a distância focal da lente côncavo-convexa 3;
Para a lente 3, teremos:
Passo 6
Determine o tipo de imagem (real ou virtual) da lente côncavo-convexa 3;
Como , a imagem é real.
Passo 7
Determine a distância focal da lente bicôncava 4;
Para a lente 4, teremos:
Passo 8
Determine o tipo de imagem (real ou virtual) da lente bicôncava 4;
Como , a imagem é virtual.
Passo 9
Determine a distância focal da lente no-côncava 5;
Para a lente 5, teremos:
Passo 10
Determine o tipo de imagem (real ou virtual) da lente no-côncava 5;
A imagem é virtual.
Passo 11
Determine a distância focal da lente convexo-côncava 6;
Para a lente 6, teremos:
Passo 12
Determine o tipo de imagem (real ou virtual) da lente convexo-côncava 6.;
A imagem é virtual.
Resposta
A imagem é real.
A imagem é real.
A imagem é real.
A imagem é virtual.
A imagem é virtual.
A imagem é virtual.
Exercício Resolvido #12
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 64
A tabela mostra seis modos possíveis de combinar lentes convergentes e divergentes em um arranjo como o da figura abaixo. (Os pontos e são os pontos focais das lentes 1 e 2.)
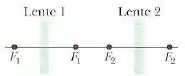
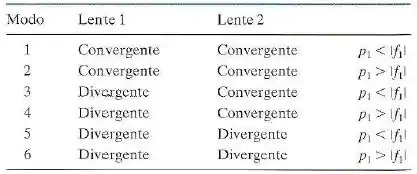
Um objeto se encontra a uma distância à esquerda da lente 1, como a figura abaixo.
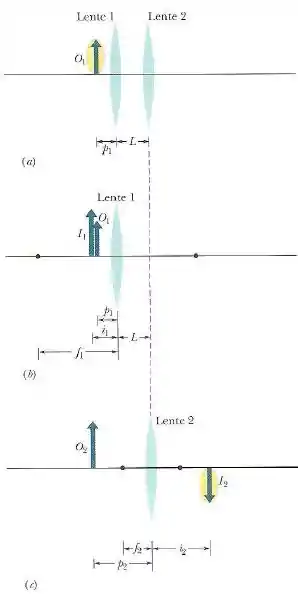
Para que combinações podemos determinar, sem fazer nenhum cálculo, se a imagem final (produzida pela lente 2) está à esquerda ou à direita da lente 2 e se tem a mesma orientação que o objeto ou a orientação oposta?
Para essas combinações “fáceis” indique a localização da imagem como “à esquerda” ou “à direita” e a orientação como “a mesma” ou “invertida”.
Passo 1
Para que combinações podemos determinar, sem fazer nenhum cálculo, se a imagem final (produzida pela lente 2) está à esquerda ou à direita da lente 2 e se tem a mesma orientação que o objeto ou a orientação oposta?
Esse é uma boa questão para exercitar as regras para construir a imagem formada por uma lente. Como não podemos fazer cálculos, vamos resolver esse problema a partir dos desenhos de cada combinação, ok?
IMPORTANTE! Como não sabemos exatamente a distância entre as lentes e a distância focal de cada uma, se a imagem , produzida pela Lente 1, se formar no espaço entre as lentes, não temos como saber exatamente como será a imagem formada pela Lente 2. Isso porque se a imagem estiver à frente do ponto teremos um tipo de imagem, e se a imagem estiver entre o ponto e a Lente 2, teremos outro tipo de imagem.
Combinação 1:
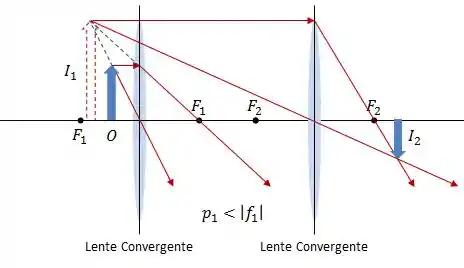
Combinação 2:
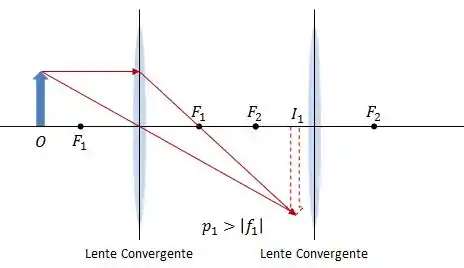
Aqui a imagem se formou entre as duas lentes, logo, não temos como saber ao certo como será a imagem final .
Combinação 3:
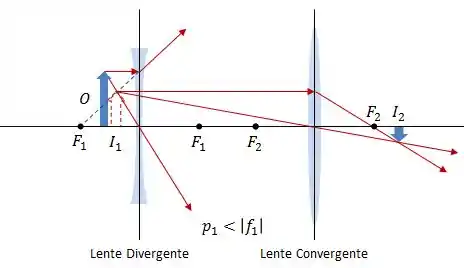
Combinação 4:
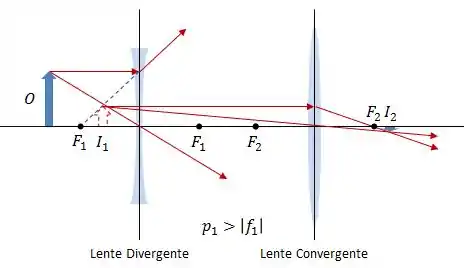
Combinação 5:
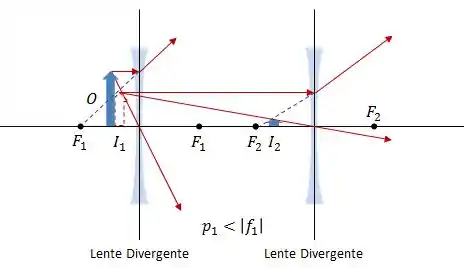
Combinação 6:
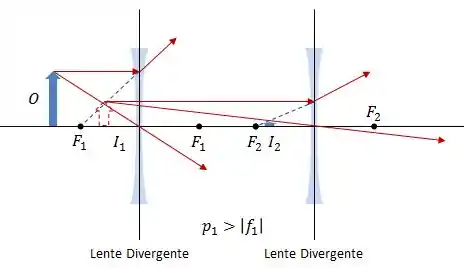
Como podemos ver, em todos os casos nós conseguimos saber onde a imagem final será formada e a sua orientação, exceto a combinação 2.
Passo 2
Para essas combinações “fáceis” indique a localização da imagem como “à esquerda” ou “à direita” e a orientação como “a mesma” ou “invertida”.
As combinações 1, 3 e 4 apresentam a imagem final à direita da Lente 2, e com a orientação da imagem invertida. Enquanto as combinações 5 e 6 apresentam a imagem final à esquerda da Lente 2, e com a mesma orientação do objeto.
Resposta
Todas, exceto a combinação 2.
1,3 e 4: à direita, invertida / 5 e 6: à esquerda, a mesma.
Exercício Resolvido #13
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 75
Na figura abaixo um grão de areia está a da lente delgada 1, sobre o eixo central comum às duas lentes.

A distância entre o ponto focal e a lente é para as duas lentes, que estão separadas por uma distância de .
Qual é a distância entre a lente 2 e a imagem que essa lente produz do grão de areia?
Determine se a imagem está à esquerda ou à direita da lente 2, é real ou virtual e é invertida ou não-invertida em relação ao grão de areia.
Passo 1
Qual é a distância entre a lente 2 e a imagem que essa lente produz do grão de areia?
Vamos começar pela Lente 1, aplicando a seguinte equação:
Rearrumando isso, encontraremos o seguinte:
Onde:
Obs.: Como a Lente 1 é convergente, o valor de será positivo.
Substituindo os valores, teremos:
Como o valor de é negativo, significa que a imagem é virtual, ou seja, ela se forma à esquerda da Lente 1.
Passo 2
Agora vamos para a Lente 2!
A distância será dada por:
Onde é a distância entre as lentes, e . Logo:
Obs.: Como a Lente 2 é divergente, o valor de será negativo. Logo. .
Agora basta utilizar a equação abaixo para descobrir o valor de :
Arrumando isso, teremos:
Logo, a distância entre a Lente 2 e a imagem final é de ;
Passo 3
Determine se a imagem está à esquerda ou à direita da lente 2.
Como o valor de é negativo, significa que a imagem é virtual, ou seja, será formada à esquerda da lente 2.
Passo 4
Determine se a imagem é real ou virtual.
Como vimos no item anterior, como o valor de é negativo, significa que a imagem é virtual.
Passo 5
Determine se a imagem é invertida ou não-invertida em relação ao grão de areia.
Para definir se a imagem é invertida ou não, precisamos calcular a ampliação lateral total. Se a mesma for positiva, significa que a imagem é não-invertida em relação ao grão de areia. Se a ampliação lateral total for negativa, significa que a imagem é invertida em relação ao grão.
A ampliação lateral total é dada por:
Onde:
Logo:
Substituindo os valores, teremos:
Como é positivo, a imagem final terá a mesma orientação que o objeto.
Resposta
A imagem final está à esquerda da Lente 2.
A imagem final é virtual.
A imagem final terá a mesma orientação que o objeto.
Exercício Resolvido #14
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 73
Na figura abaixo, o boneco (o objeto) está sobre o eixo central comum de três lentes delgadas simétricas, que estão montadas nas regiões limitadas por linhas tracejadas.
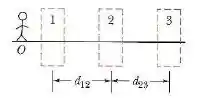
A lente 1 está montada na região mais próxima de , a uma distância do boneco. A lente 2 está montada na região do meio, a uma distância da lente 1. A lente 3 está montada na região mais afastada de , a uma distância da lente 2.
Cada problema da tabela abaixo se refere a uma combinação diferente de lentes e a valores diferentes das distâncias, que são dadas em centímetros. O tipo de lente é indicado como no caso de uma lente convergente e como no caso de uma lente divergente; o número que se segue a ou é a distância entre a lente e um dos pontos focais (o sinal da distância focal não está inciado).
Obs.: Utilize os dados referentes ao problema 113.
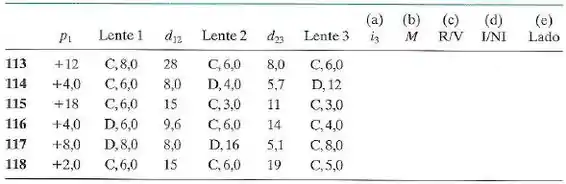
Determine a distância entre o objeto e a imagem produzida pela lente 3 (a imagem final produzida pelo sistema) e a ampliação lateral total do sistema, incluindo o sinal.
Determine também se a imagem é real ou virtual , se é invertida ou não-invertida e se está do mesmo lado da lente que o objeto ou está do lado oposto .
Passo 1
Determine a distância entre o objeto e a imagem produzida pela lente 3 (a imagem final produzida pelo sistema).
Vamos analisar cada lente separadamente:
Lente 1:
Onde:
Logo:
Lente 2:
Para a lente 2, a distância será dada por:
Além disso, a distância focal da lente 2 é . Logo:
Lente 3:
Para a lente 3, a distância será dada por:
Além disso, a distância focal da lente 3 é . Logo:
Passo 2
Determine a ampliação lateral total do sistema, incluindo o sinal.
A ampliação lateral total do sistema será:
Onde:
Logo:
Substituindo os valores, teremos:
Passo 3
Determine se a imagem é real ou virtual .
Como o valor de é positivo, então a imagem é real .
Passo 4
Determine se a imagem invertida ou não-invertida .
Como o valor de é positivo, então a imagem é não-invertida .
Passo 5
Determine se está do mesmo lado da lente que o objeto ou está do lado oposto .
Como a imagem é real, ela está formada do lado oposto ao do objeto .
Resposta
A imagem é real .
A imagem é não-invertida .
A imagem está formada do lado oposto ao do objeto .