Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Identidade de Parseval

Ver Teoria
Exercício 17123456789101112131415161819

Enunciado

Passo 1

a)

Beleza, agora vamos montar o problema. Ele quer a série de Fourier dessa função. Então precisamos fazer

f x = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n π x L + b n sen ⁡ n π x L

Com

a n = 1 L ∫ - L L f x cos ⁡ n π x L d x ,     n = 0,1 , 2,3 …

b n = 1 L ∫ - L L f x sen ⁡ n π x L d x ,     n = 1,2 , 3 …

Como já vimos o período é 2 π , então

2 L = 4

L = 2

Passo 2

Vamos começar fazendo a 0

a 0 = 1 L ∫ - L L f x d x

Substituindo L

a 0 = 1 2 ∫ - 2 2 f x d x

Substituindo o valor de f x temos uma integral só naquela parte onde não é 0

a 0 = 1 2 ∫ - 2 0 1 d x + ∫ 0 2 2 d x = 3

Separando esse módulo

Passo 3

Vamos agora para a n

a n = 1 2 ∫ - 2 2 f x cos ⁡ n π x 2 d x

Substituindo o valor de f x temos uma integral simples de resolver e a soma é igual a zero, mas cuidado, ela não é par.

a n = 1 2 ∫ - 2 0 cos ⁡ n π x 2 d x + ∫ 0 2 2 cos ⁡ n π x 2 d x = 0

Passo 4

Vamos agora achar b n

b n = 1 2 ∫ - 2 2 f x sen ⁡ n π x 2 d x

Substituindo o valor de f x temos uma integral simples de resolver

b n = 1 2 ∫ - 2 0 1 sen ⁡ n π x 2 d x +   ∫ - 2 0 2 sen ⁡ n π x 2 d x

Resolvendo:

b n = 1 2 n π 2 - 2 cos ⁡ n π

Simplificando:

b n = 1 n π 1 - - 1 n

Passo 5

Para A nossa série de Fourier vai ser

f x = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n x + b n sen ⁡ n x

Substituindo os valores dos coeficientes vão ser

S x = 3 2 + ∑ n = 1 ∞ 2 2 n - 1 π sen ⁡ ( 2 n - 1 ) π x 2

Passo 6

b)

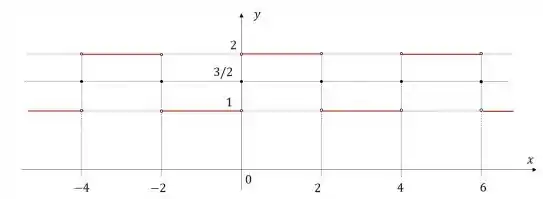
Veja que é simples construir o gráfico, porem temos um problema nos pontos de descontinuidade, certo?

Vamos lembrar que nos pontos de descontinuidade:

f x = f x - + f ( x + ) 2

E nos outros pontos, temos que:

f x + P = f x

Então, podemos escrever:

S x =   1 ,       x   ∈   ] - 2 + 4 k , 4 k [ 3 2 ,     x = 2 k   2 ,       x   ∈   ] 4 k , 4 k + 2 [ ,       o n d e   k ∈ Z

Com isso o gráfico é:

Passo 7

c)

Vamos agora utilizar a identidade de Parseval para fazer essa questão.

Vamos relembrar dela, ok?

1 L ∫ - L L f x 2 d x = a 0 2 2 + ∑ n = 1 ∞ ( a n 2 + b n 2 )

Substituindo os valores de a 0 ,   a n ,   b n :

9 2 + ∑ n = 1 ∞ 4 2 n - 1 2 π 2 = 1 2 ∫ - 2 0 1 d x + ∫ 0 2 4 d x = 10 2  

Então, simplificando:

4 π 2 ∑ n = 1 ∞ 1 2 n - 1 2 = 10 2 - 9 2 = 1 2

Assim:

∑ n = 1 ∞ 1 2 n - 1 2 = π 2 8  

Passo 8

d)

Basta utilizarmos:

f x + P = f x

Nesse caso, P = 4

Assim:

S 2014 = S 504 ⋅ 4 - 2 = S - 2 = 3 2

Analogamente para 2015 :

S 2015 = S 504 ⋅ 4 - 1 = S - 1 = f ( - 1 ) = 1

Resposta

a)

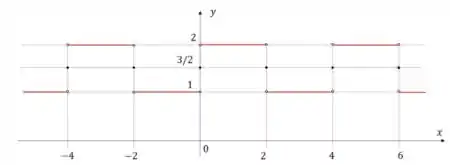
S x = π 4 + ∑ n = 1 ∞ 2 n sen ⁡ n π 2 + 4 π n 2 cos ⁡ n π 2 - 4 π n 2 cos ⁡ n x

b)

c)

∑ n = 1 ∞ 1 2 n - 1 2 = π 2 8  

d)

S 2014 = 3 2

S 2015 = 1