Introdução à Cinemática de Corpos Rígidos
Produzido por Pablo RicardoTeoria
Introdução
Repare neste brinquedo:

Ele se move em uma trajetória circular, mas mantendo sempre a posição na horizontal. Este tipo de movimento recebe um nome e cada tipo de deslocamento necessita de uma análise diferente.
É isso que vamos aprender neste capítulo, quais os movimentos possíveis de um corpo e como identificá-los para aplicar a análise mais adequada para cada caso.
Então, partiu!
O Corpo Rígido
Um corpo rígido é aquele que pode acontecer o que for que ele continuará com o mesmo formato e com suas mesmas dimensões. Ou seja, um corpo rígido é um sistema composto de partículas sólidas que não se deformam. E o que significa um corpo não se deformar? Significa que a distância entre todos os pontos desse mesmo corpo não muda com o passar do tempo.
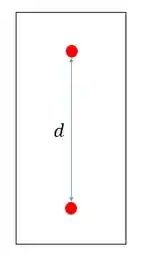
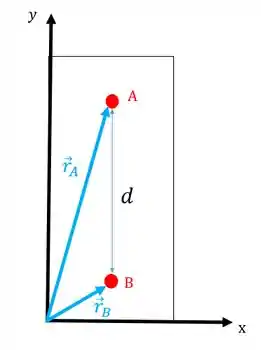
Mas o que isso significa na prática? Se fixarmos um eixo no próprio corpo e marcarmos o vetor posição de cada ponto com relação a origem deste eixo, esse vetor vai continuar constante mesmo se o corpo se mover.
Vamos girar um pouco esse corpo:
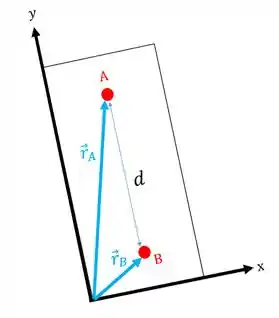
Repare que os vetores posição e permanecem os mesmos!
Entendido isso, vamos entender como funciona o movimento de um corpo rígido.
Movimento do Corpo Rígido
- Translação
- Rotação em torno de um eixo fixo
- Movimento Plano Geral
Vamos usar o nosso corpo rígido e marcar dois pontos nele:
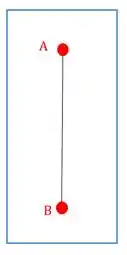
Agora, vamos imaginar que este corpo teve um deslocamento :
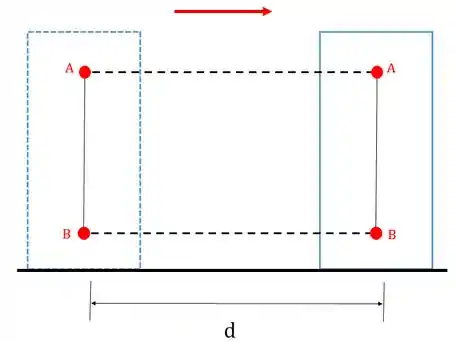
Repare que ao se deslocar, a linha que liga os pontos e antes do deslocamento e a linha que liga estes mesmo pontos após o deslocamento são paralelas. Quando isso acontece dizemos que o corpo sofreu um movimento de translação.
Existem dois tipos de translação: a retilínea e a curvilínea. Na translação retilínea, a trajetória que cada ponto que pertence ao corpo rígido faz é sempre uma reta, como aconteceu no exemplo acima:
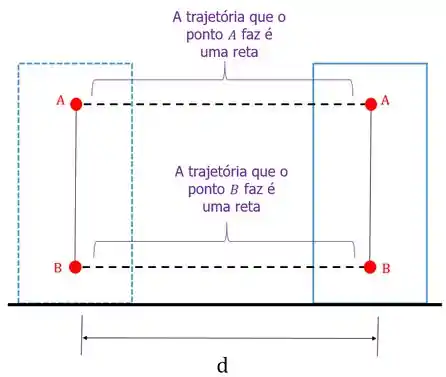
A translação curvilínea ocorre quando a trajetória que os pontos do corpo fazem é curvilínea:
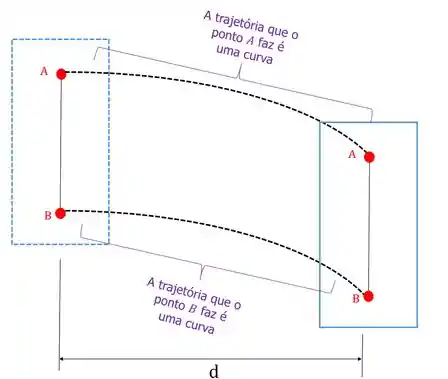
Este movimento pode ocorrer quando tem placas oscilando com hastes paralelas, assim:
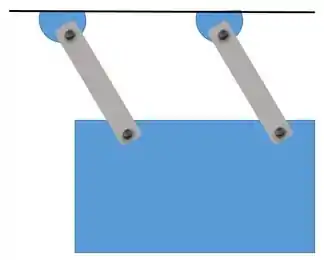
Este movimento ocorre quando um corpo gira em torno de um eixo de rotação ou um ponto. Quando isso acontece, todos os pontos que pertencem ao corpo realizam movimentos circulares, menos os pontos que estão sobre o eixo de rotação:
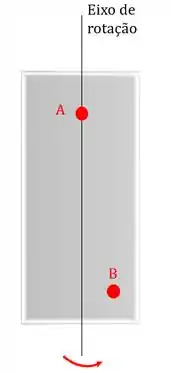
Quando o corpo gira em torno do eixo de rotação, o ponto também gira (realizando um movimento circular), já o ponto , que está sobre o eixo, continua na mesma posição.
Este movimento ocorre quando o corpo realiza rotação e translação ao mesmo tempo. Nesses casos, a translação ocorre com relação a um plano de referência e a rotação ocorre com relação a um eixo perpendicular ao plano.
É o caso de um disco girando em torno de seu centro e ao mesmo tempo se deslocando ao longo de uma reta:
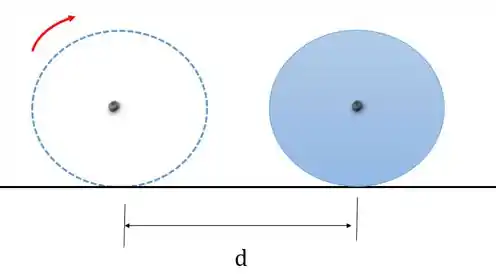
Vamos fazer uma revisão rapidinha de cinemática, pois nos será muito útil para analisar o movimento de corpos rígidos!
Revisão de Cinemática
Primeiramente, você lembra o que é cinemática? Cinemática é o estudo do movimento, mas sem levar em conta as forças que causam o tal deslocamento de um corpo.
- Movimento Retilíneo:
Ocorre quando o corpo se desloca ao longo de uma reta. Para analisar este movimento temos que lembrar o que é posição, deslocamento, velocidade e aceleração.
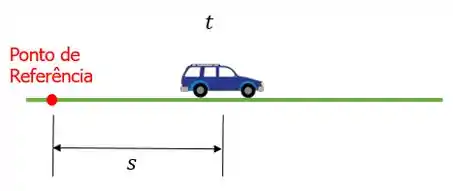
- Posição: é a distância do corpo que estamos analisando até um ponto de referência e é representada pela letra :
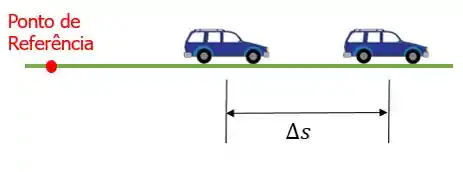
- Deslocamento: a variação da posição () com o passar do tempo:
- Velocidade: a variação da posição (o deslocamento) com relação ao tempo. Mas lembre-se que tomamos valores infinitesimais de tempo e de deslocamento, por isso usamos o conceito de derivada:
- Aceleração: é só derivarmos a velocidade com relação ao tempo:
- Relação entre deslocamento, velocidade e aceleração:
- Aceleração constante: quando a aceleração é constante temos as seguintes equações:
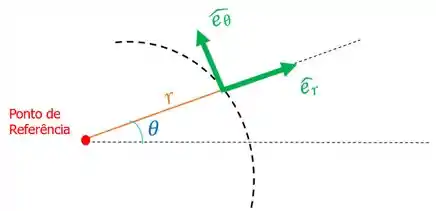
- Coordenadas Polares: nessas coordenadas a gente cria dois vetores unitários perpendiculares entre si: um na direção do raio da trajetória que vamos chamar de e outro que é tangente à trajetória que vamos chamar de .
- Posição: vamos colocar a equação da posição e a equação do ângulo em função das coordenadas polares, assim:
- Velocidade: quando derivamos a equação da posição obtemos a velocidade:
- Aceleração: é só derivarmos a expressão da velocidade:
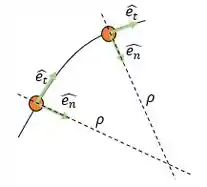
- Coordenadas Tangenciais e Normais: os nossos vetores unitários perpendiculares entre si vão ser um normal à trajetória cujo sentido positivo vai ser sempre apontando para o centro da curva e que vamos chamar de; outro tangente à trajetória cujo sentido positivo aponta para o sentido de crescimento do deslocamento e que vamos chamar de .
- Velocidade: sabemos que a velocidade é sempre tangente à trajetória, então a velocidade vai ser sempre na direção tangencial:
- Aceleração: é só derivar a equação da velocidade:
Ou podemos separar nas componentes radial e tangencial:
Podemos separar em dois componentes, uma tangencial e outra radial:
E o módulo da velocidade é:
A aceleração tem uma componente tangencial e outra normal:
- Componente tangencial muda o módulo da velocidade e é sempre tangente à trajetória. Vamos chamar esta componente de aceleração tangencial e seu módulo é:
- Componente normal muda direção e o sentido da velocidade e sempre aponta para o centro da trajetória. Vamos chamar esta componente de aceleração centrípeta e seu módulo é:
O é o raio da curvatura!
Isso foi uma revisão de tudo que vimos até agora e que vai nos ajudar a entender melhor o movimento do corpo rígido.
Partiu exercícios? Então, vamos lá!!!
O Corpo Rígido
Movimento do Corpo Rígido
Revisão de Cinemática
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Dinâmica, 6º ed. RJ: LTC, 2012, pp. 25-2/25.
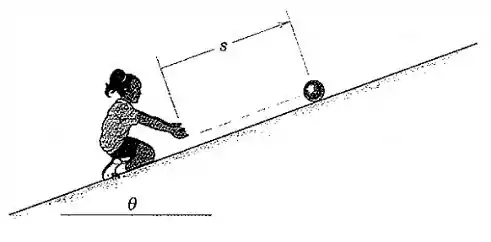
Uma menina rola uma bola para cima em um plano inclinado e deixa esta retornar para ela. Para o ângulo e a bola em questão, a aceleração da bola ao longo da inclinação é constante em , dirigida para baixo no plano inclinado. Se a bola é liberada com uma velocidade de , determine a distância em que esta se move para cima no plano inclinado antes de inverter o seu sentido e o tempo total necessário para a bola retornar à mão da criança.
Passo 1
Nesse exercício a aceleração é constante, então podemos usar uma equação daquele conjunto que temos para aceleração constante. Repare que temos a velocidade inicial e ele quer saber no primeiro item a distância percorrida.
Vamos usar uma equação que tenha essas variáveis:
Vamos ver o que temos de dados do exercício. Temos a velocidade inicial que é , temos também a aceleração que é , onde esse sinal de menos é porque foi dito que a aceleração é dirigida para baixo no plano inclinado e a bolinha está subindo o plano. Com essa mesma informação, vemos que não é necessário decompor a aceleração, pois ela está ao longo do plano.
Consideramos a gravidade como . Agora vamos analisar as informações a mais que ele nos deu: ele disse que quer saber a distância em que a bola se move para cima no plano inclinado antes de inverter o seu sentido. O que isto quer dizer?
Quando a bola inverte seu sentido, ou seja, quando ela começar a descer o plano, ela precisa ter a velocidade igual a zero. Então, no momento de transição temos que .
Falta agora sabermos qual a posição inicial da bola. Mas repare que a bola é lançada a partir de um ponto e retorna para este mesmo ponto. Ou seja, podemos arbitrar que a posição inicial começa no zero:
Pronto, agora podemos calcular a posição final da bolinha:
Passo 2
Nosso próximo é descobrir o tempo necessário para que a bola retorne à mão da criança. Repare que o tempo que a bolinha leva para subir é o mesmo tempo que ela levará para descer, então podemos dizer que o tempo total é:
E:
Portanto,
Então, vamos calcular o tempo de subida. Mas qual equação usar? Nós temos aceleração, velocidade e queremos saber o tempo:
Vamos substituir: , e :
Então, o tempo total será:
Resposta
Exercício Resolvido #2
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 22-2/6.
A aceleração de uma partícula é dada por , onde é a aceleração em metros por segundo ao quadrado e é uma constante, e é em metros. Determine a velocidade da partícula como uma função de sua posição . Avalie sua expressão para se
e as condições iniciais no instante t = 0 são e .
Passo 1
Vamos analisar quais variáveis foram dadas para ver uma equação que as relacionem. Temos a aceleração em função da posição, velocidade e posição iniciais.
Então, vamos ter que usar a seguinte equação:
Vamos integrar o lado esquerdo com relação a posição e lado direito com relação à velocidade:
Sabemos que e . E vamos substituir :
Vamos ter:
Podemos arrumar esta nossa equação isolando o , pois é o que queremos determinar:
Passo 2
Nosso próximo é substituir o valor , , , na equação que achamos para determinar a velocidade:
Resposta
Exercício Resolvido #3
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 12-12.22
A aceleração de um foguete em movimento ascendente é dado por , onde é dado em metros. Determine a velocidade do foguete quando . Inicialmente (quando ), e .

Passo 1
Vamos começar analisando quais variáveis foram dadas no enunciado para ver uma equação que as relacionem. Temos a aceleração em função da posição, velocidade e posição iniciais.
Então, vamos ter que usar a seguinte equação:
Vamos integrar o lado esquerdo com relação a posição e lado direito com relação à velocidade:
Sabemos que e . E vamos substituir :
Vamos ter:
Podemos isolar , pois é o que queremos determinar:
Passo 2
Nosso próximo é substituir o valor de na equação que achamos para determinar a velocidade do foguete:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 46-12.113
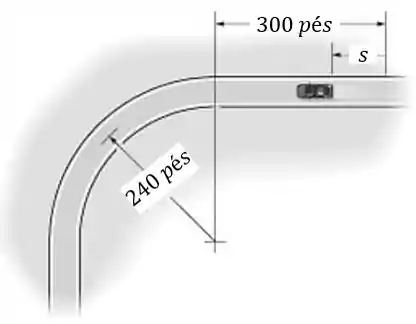
A velocidade de um automóvel, inicialmente em repouso em , varia de acordo com , onde é dado em segundos. Determine os módulos da velocidade e da aceleração do carro quando .
Passo 1
O enunciado nos deu a aceleração do carro como uma função do tempo:
Então, no tempo vamos ter o seguinte valor para aceleração:
E a velocidade? Se precisamos derivar a velocidade com relação ao tempo para achar a aceleração... Se o que temos é a aceleração, como fazemos para achar a velocidade? É isso aí, temos que integrar:
Considerando :
Então, no tempo :
Passo 2
Agora, repare pelo desenho que o carro anda em um trecho retilíneo e depois começa a fazer uma trajetória circular. Temos que analisar se em o carro está na parte reta ou já entrou na curva. Para isso, vamos achar a posição final do carro.
Sabemos que a velocidade é a derivada do deslocamento com relação ao tempo. Então, se temos a equação da velocidade em função do tempo, como iremos calcular o deslocamento? É só integrar a equação da velocidade:
O enunciado nos disse que o carro parte do repouso e, então:
Então, no tempo vamos ter que:
Ou seja, o carro percorreu toda a parte reta e entrou na curva!
Passo 3
A velocidade final no tempo não muda independentemente do movimento se dar numa reta ou numa curva. Mas.... A aceleração não será a mesma. Lembra que o movimento retilíneo pode possuir duas componentes: a aceleração centrípeta e a aceleração tangencial.
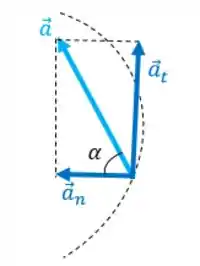
E por que eu disse pode possuir? Porque a componente tangencial só existe quando há variação de velocidade. O que ocorre no nosso caso, pois o carro começa com uma velocidade inicial zero e desenvolve uma velocidade que varia em função do tempo.
Então, vamos calcular cada componente da aceleração e depois achar a resultante.
No movimento curvilíneo a aceleração tangencial é calculada usando a equação que foi dado no enunciado para:
A aceleração centrípeta é calculada usando a seguinte fórmula:
Onde, é o raio da curvatura. No nosso caso .
A velocidade nós vimos que não muda, então . Portanto, a aceleração centrípeta será:
Vamos calcular o módulo da aceleração agora: