Movimento curvilíneo
Produzido por Pablo RicardoTeoria
O movimento curvilíneo acontece em uma trajetória curva, que pode ser circular ou parabólica. No nosso dia a dia temos vários exemplos de movimento curvilíneo, como quando uma moto faz uma curva de uma estrada! Mas… como poderemos analisar esse movimento? 😖

Quando o movimento é curvo, teremos que analisar o problema de uma forma diferente. É isso que vamos aprender hoje!
📢 Clique para ver mais:
Posição e Deslocamento Vetoriais
Em um movimento curvo, é importante tratarmos de grandezas vetoriais. Isso porque neste tipo de movimento, para cada ponto da trajetória o vetor terá um módulo, uma direção e um sentido! Então imagine um carro fazendo uma curva:
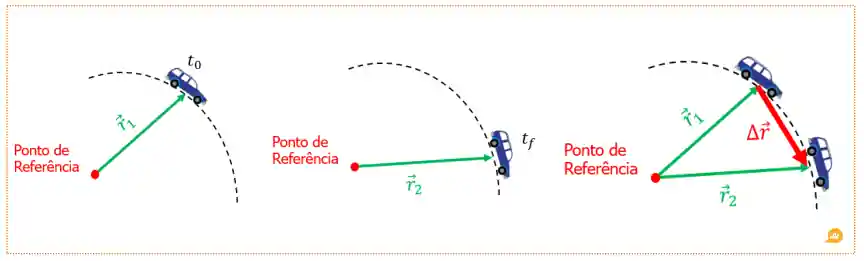
Para determinarmos a posição, escolhemos um ponto de referência e traçamos um vetor deste ponto até o carro, como mostra a primeira figura. Dizemos que
Velocidade Vetorial
A velocidade média é a variação da posição dividida pelo tempo. Para o cálculo da velocidade média vetorial, a variação da posição será o nosso vetor
Se tomarmos um
Quando a variação de tempo tende a zero, o vetor
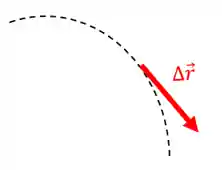
Repare que a velocidade
Bora continuar esse papo nesse vídeo super completo que o Responde Aí preparou pra você? 👇
Aceleração Vetorial
A aceleração mede o quanto a velocidade varia com o passar do tempo. Portanto, só existe aceleração se houver variação da velocidade. Mas e a aceleração vetorial? Vamos usar a velocidade vetorial para calcular:
Se fizermos ∆t tender a zero, vamos achar a aceleração instantânea que é a aceleração naquele ponto específico que estamos analisando:
A aceleração será responsável por fazer o corpo realizar o movimento curvilíneo, ou seja, é a aceleração que provoca a mudança de sentido e direção do vetor velocidade ao longo da trajetória, assim:
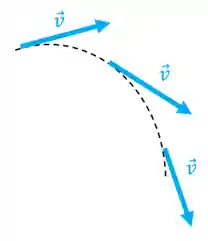
A aceleração sempre vai ter uma componente apontando para o centro da curva que vamos chamar de aceleração centrípeta e esta componente será responsável por mudar o sentido e a direção do vetor velocidade. O módulo da aceleração centrípeta é:
Onde, R é o raio da trajetória e v é o módulo da velocidade. E somente quando ocorrer um aumento ou diminuição da velocidade, a aceleração terá uma componente tangencial à trajetória que vamos chamar de aceleração tangencial. A aceleração tangencial é calculada por:
Movimento de um Projétil
O movimento de um projétil se da da seguinte forma:
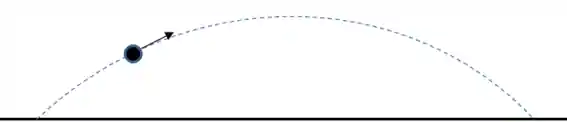
Quando um projétil é lançado, ele realiza dois movimentos perpendiculares entre si e simultâneos. Para facilitar, vamos olhar para cada movimento separadamente: um na horizontal e outro na vertical. Para isso, vamos decompor o vetor velocidade:
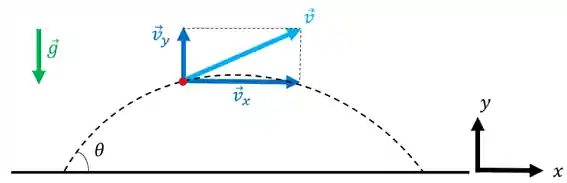
Movimento na Vertical
Na vertical teremos um movimento retilíneo que sofre a ação da gravidade, logo a aceleração é constante. Se quisermos calcular a velocidade na vertical
Já se quisermos calcular a altura do projétil, vamos usar esta fórmula:
Caso você tenha que relacionar a altura do projétil com a sua velocidade vertical, mas sem ter dado nenhum de tempo, use essa fórmula aqui:
Movimento na Vertical
Na horizontal teremos um movimento que não sofre aceleração nenhuma e, portanto, é um movimento retilíneo uniforme. Como não há aceleração, a velocidade horizontal é constante.
Se quisermos calcular a posição do projétil no eixo x, temos:
Repare que a velocidade de lançamento faz um certo ângulo θ com a horizontal:
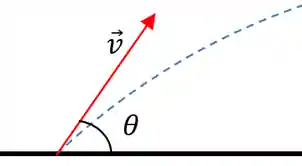
Sendo assim:
Agora vamos praticar com exercícios?
Aceleração Vetorial
Movimento de um Projétil
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2013, 34, 2/61
No instante , a velocidade de uma partícula que se desloca no plano é . No instante , a sua velocidade torna-se . Determine o módulo de sua aceleração média durante este intervalo e o ângulo dado pela aceleração média com o eixo positivo .
Passo 1
Sabendo que a aceleração média é:
Passo 2
Agora vamos calcular o módulo da aceleração média:
Passo 3
Assim, o ângulo será:
Como as duas componentes da aceleração são negativas, ela estará no terceiro quadrante. Então o ângulo certo é .
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 34, 2/67
O vetor posição de um ponto que se move no plano é dado por:
Onde é expresso em metros e é expresso em segundos. Determine o ângulo entre a velocidade e a aceleração quando e .
Passo 1
Vamos calcular a velocidade derivando o vetor:
E para achar a aceleração é só derivarmos de novo:
Passo 2
Para
E:
Para calcular o ângulo entre eles, temos que achar o módulo destes vetores:
Assim:
Assim:
Passo 3
E para , vamos ter que:
E a aceleração:
Opa!
Nesse caso, nem precisamos fazer contas. Perceba que os vetores tem a mesma direção, sendo assim, são paralelos. Então, o ângulo entre eles vai ser zero:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 34, 2/62
Uma partícula que se move em um movimento curvilíneo tem coordenadas em milímetros que variam com o tempo em segundos de acordo com e . Determine os módulos da velocidade e aceleração e os ângulos que estes vetores fazem com o eixo quando .
Passo 1
O vetor deslocamento é dado por:
Sabendo que a velocidade é a derivada da posição no tempo, temos que:
E a aceleração é a derivada da velocidade com relação ao tempo:
Passo 2
Para , vamos ter que:
E a aceleração fica:
Passo 3
O módulo do vetor velocidade vai ser:
E o módulo do vetor aceleração é:
Passo 4
Assim, o ângulo que o vetor velocidade faz com o eixo é:
Passo 5
E o ângulo que o vetor aceleração faz com o eixo é:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 34, 2/63
Uma partícula que se desloca em movimento bidimensional tem coordenadas em milímetros dadas por e , onde é o tempo em segundos. Determine os módulos da velocidade e a aceleração e o ângulo entre estes dois vetores no instante .
Passo 1
O vetor deslocamento é dado por:
Sabendo que a velocidade é a derivada da posição no tempo, temos que:
E a aceleração é a derivada da velocidade com relação ao tempo:
Passo 2
Para , vamos ter que:
E:
Assim:
E:
Passo 3
Assim, o ângulo será:
Assim:
Observação:
Quando você for calcular o valor de , o valor que estará em radianos. Mas perceba que no final, quando usamos a função, retornamos um valor em graus. Enfim, são apenas ajustes na calculadora!
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2013, 34, 2/66
Os movimentos e das guias e com ranhuras em ângulo reto controlam o movimento curvilíneo do pino de conexão, que desliza nas duas ranhuras. Por um curto intervalo de tempo, os movimentos são regidos por , onde e são em milímetros e é em segundos. Calcule o módulo da velocidade e aceleração do pino para . Desenhe a direção da trajetória e indique a sua curvatura para esse instante.
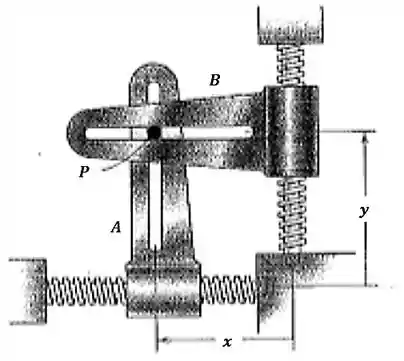
Passo 1
O vetor deslocamento é dado por:
Sabendo que a velocidade é a derivada da posição no tempo, temos que:
E a aceleração é a derivada da velocidade com relação ao tempo:
Passo 2
Para , vamos ter que a velocidade será de:
E a aceleração vai ser igual a:
Passo 3
Com isso, podemos calcular o módulo da velocidade:
E:
Passo 4
Então, o nosso desenho vai ficar assim:
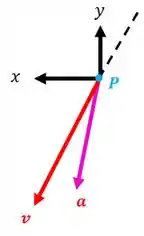
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 39, 2/70
Se o cano da espingarda mostrada aponta para o ponto , calcule a distância abaixo de até o ponto onde a bala incide. A velocidade de saída no disparo da bala é de .
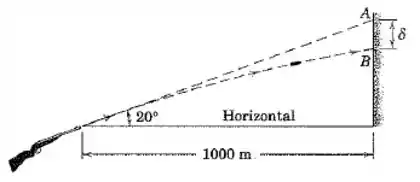
Passo 1
Para resolver essa questão, precisamos utilizar a fórmula do lançamento horizontal. Como o que interessa para nós é a altura, vamos usar a fórmula da altura do projétil.
O tempo, nós podemos pegar da fórmula da velocidade horizontal do projétil:
Logo:
Substituindo na fórmula da parcela vertical:
Além disso, precisamos lembrar que:
Substituindo na nossa fórmula:
Ou seja:
Passo 2
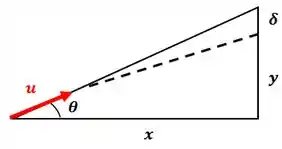
Pelo triângulo acima, podemos dizer que:
Passo 3
Então, vamos pegar a nossa fórmula para que encontramos no passo e adicionar dos dois lados da igualdade:
Substituindo os valores do enunciado:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 39, 2/94
O jogador de basquete gosta de arremessar seu lance livre em um ângulo com a horizontal como mostrado. Que velocidade inicial fará com que a bola passe através do centro do aro?
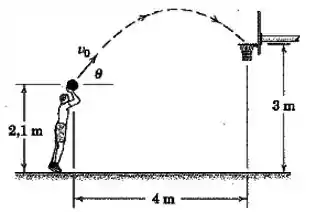
Passo 1
Nós não sabemos quanto vale . Então vamos escrever tudo em função de . Assim, a componente do movimento será:
Sendo
Vamos calcular agora o tempo que o móvel leva pra alcançar a distância horizontal de
Guarde esse tempo, pois esse é o tempo que a bola leva voando.
Passo 2
Agora vamos usar o deslocamento vertical. A bola sai da coordenada e atinge a coordenada
Assim, podemos dizer que:
Para o tempo
Organizando:
Passo 3
Assim:
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 39, 2/97
Um projétil é lançado em um fluido experimental no instante . A velocidade inicial é e o ângulo com a horizontal é . O arrasto sobre o projétil resulta em um termo de aceleração , onde é a constante e é a velocidade do projétil. Determine as componentes e da velocidade e do deslocamento como funções do tempo. Qual é a velocidade final? Inclua os efeitos da aceleração gravitacional.
Passo 1
Considerando a aceleração da gravidade, temos a seguinte aceleração total:
Onde:
Assim:
Passo 2
Assim:
Só que:
Assim:
Só que:
Assim:
E:
Passo 3
Em
Assim:
Passo 4
Com as componentes da velocidade:
Vamos calcular a velocidade terminal do móvel, para tendendo a infinito: