Equilíbrio em duas Dimensões
Produzido por Pablo RicardoTeoria
Introdução
Agora vamos falar sobre algo chamado Equilíbrio... Mas para que serve isso?
Imagine uma tábua de peso desprezível que pode girar com relação a um pino posicionado na metade do seu comprimento. Aí você resolve colocar um bloco de em uma das extremidades dessa tábua. O que irá acontecer com ela?

Ela vai cair para o lado mais pesado, certo? Isso acontece porque na sua outra extremidade não tem nada para compensar o peso do bloquinho que colocamos.
Agora você quer que está tábua fique em equilíbrio... O que é preciso fazer? Colocar um bloco de mesmo peso na outra extremidade, certo?
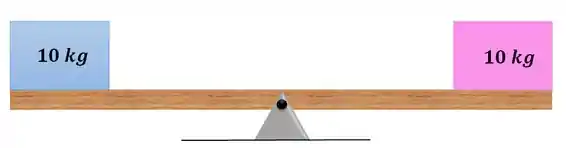
Mas e seu eu mudar o apoio de lugar:
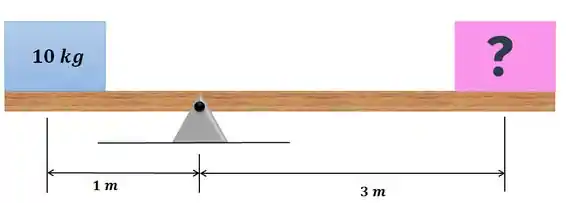
Qual é a nova massa que o bloquinho rosa deve ter para que a tábua não gire em torno do pino?
Calma! É isso que vamos aprender neste tópico, partiu?
O Diagrama de Corpo Livre
O primeiro passo para resolver qualquer questão de equilíbrio é fazer o diagrama de corpo livre, também conhecido por DCL. Mas como faço esta coisa? É só você olhar para o seu problema e isolar o corpo principal, aquele que está sofrendo a ação de várias forças. O diagrama deve mostrar todas as forças que atuam no corpo.
Vamos montar o diagrama de corpo livre da nossa tábua lá de cima. Primeiro temos que identificar qual é o corpo principal: neste nosso caso é a própria tábua, ela que está sofrendo a ação das forças peso dos bloquinhos:
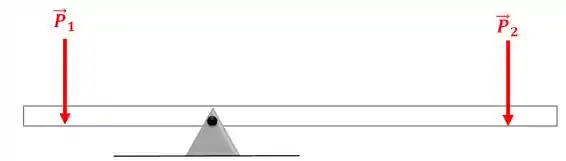
Repare que os bloquinhos foram retirados e no seu lugar foi colocada a força que cada um deles faz na tábua, essas forças são o próprio peso dos bloquinhos.
Mas eu não disse que tem que representar apenas o corpo principal do problema e retirar todos os outros? E o que esse apoio está fazendo ali? Calma, temos que retirar ele também e colocar no lugar a força que o apoio faz na tábua:
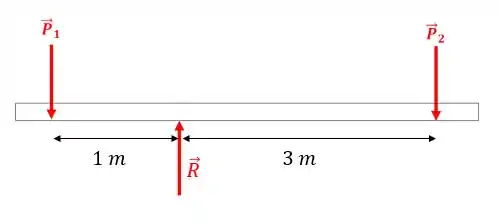
Repare que cada elemento que você retirar do problema você tem que substituir por uma força. Mas em que posição do corpo eu coloco a força?
O centro de massa ( ou ) é o ponto de um corpo que, para fins de cálculo, pode ser considerado como aquele que contêm toda a massa do corpo, por isso, podemos representar as forças no centro de massa das figuras.
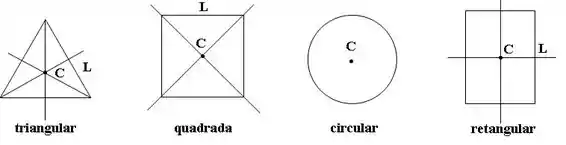
Observação: você pode encontrar por aí a definição centro de gravidade. Geralmente em cursos de Mecânica Básica, como aqui, os dois pontos são o mesmos:
Percebam que as forças peso atuam co centro de gravidade dos nossos bloquinhos.
Então, podemos entender o diagrama de corpo livre como uma maneira de limpar o nosso desenho e enxergarmos o que está acontecendo no corpo principal.
Tipos de Apoios e suas Reações
O apoio é o que sustenta a estrutura e a impede de se movimentar em certas direções. Toda vez que você impede uma estrutura de se movimentar em uma direção surge o que chamamos de reação de apoio. Existem vários tipos de apoios e para cada um vai surgir alguma reação de acordo com a direção em há o impedimento de movimento. Vamos ver os principais:
- Apoio Deslizante: permite que a estrutura se mova na direção em que o carrinho rola, mas impede o movimento na outra direção:
- Pinos: esses apoios impedem que a estrutura se mova tanto na vertical quanto na horizontal, mas permitem que ela gire em torno dele:
- Apoio fixo ou engaste: este apoio impede o movimento nas direções horizontal e na vertical e também impede que a barra gire em torno dele:

Essas são as formas possíveis que esse apoio pode aparecer para você, todas essas imagens representam a mesma coisa!!!
Além disso, repare que no nosso exemplo temos esse mesmo tipo de apoio!

Repare que esse apoio permite o movimento na horizontal, mas impede o movimento na vertical. Então, a reação de apoio vai estar na direção em que há impedimento do movimento. Dessa forma, para montar o diagrama de corpo livre é só retirar o apoio e colocar a reação vertical:

E se o apoio estiver assim na vertical?

Neste caso, o apoio permite que a barra se mova na vertical, mas impede que ela se mova na horizontal. Então, o diagrama de corpo livre fica assim:
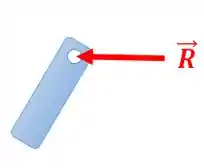
Fica ligado nisso aí!!! ![]()
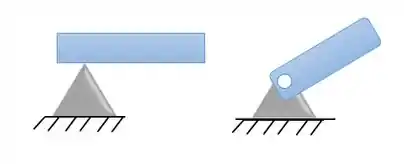
Como esses apoios impedem o movimento nas duas direções, o diagrama de corpo livre fica:
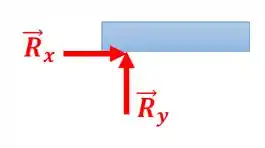

As reações de apoios surgem devido ao impedimento do movimento, então o diagrama de corpo livre fica:
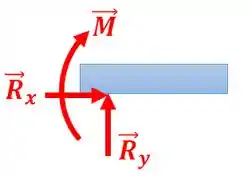
Esse momento surge devido ao apoio impedir que a estrutura gire.
Condições de Equilíbrio
Uma estrutura está em equilíbrio estático quando a resultante de todas as forças horizontais, verticais e dos momentos são nulas:
Isso acontece porque não podemos ter nenhuma aceleração que promova movimentos de translação ou rotação.
Aqui repare que podemos utilizar a equação do momento para resolver o problema proposto lá do início. Vamos fazer isso aplicando o somatório dos momentos em relação a um certo ponto:
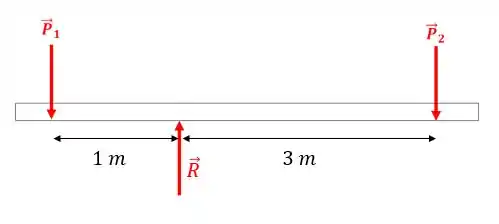
Lembre-se que
Então temos e queremos achar . Logo, faz sentido colocar o ponto de aplicação do momento exatamente no ponto de apoio:
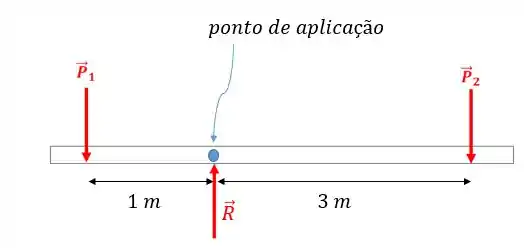
Por que isso faz sentido? Porque a força não irá gerar momento com relação a esse ponto, o que é bom já que não sabemos o valor de . Dessa forma vamos ter:
Vamos considerar o sentido anti-horário positivo:
Substituindo os valores de e :
Resolvemos o nosso problema!
Vamos fazer uns exercícios para treinar e pegar o jeito!!! ![]()
O Diagrama de Corpo Livre
Tipos de Apoios e suas Reações
Condições de Equilíbrio
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 96,3/5
O suporte deslizante é usado para apoiar partes de chapas longas enquanto elas são cortadas por uma série de bancadas. Se a chapa exerce uma força direcionada para baixo de no rolete , determine as ações verticais em e Note que a conexão em é rígida e que os pés e são tubos horizontais razoavelmente longos, com recobrimentos deslizantes.
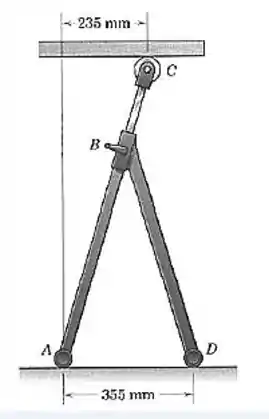
Passo 1
Fala aí, pessoal!! Vamos entender primeiro o que está acontecendo nessa situação aqui. O suporte deslizante descrito no problema é o próprio conjunto , que desliza no ponto através de um rolete.
Como as barras e são “razoavelmente longas” podemos aproximar as reações em e para forças verticais, como sugerido no enunciado.
Sabendo disso podemos fazer o sistema de forças, que é dado abaixo:
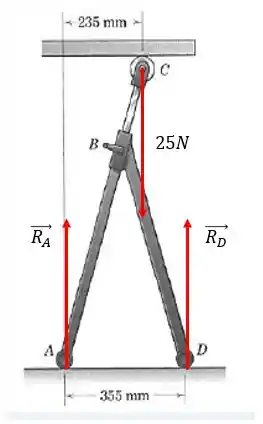
Passo 2
Temos que satisfazer a duas condições:
E:
Para o caso dos momentos, vamos escolher o ponto , assim não precisamos trabalhar com de cara, pois esta força não tem braço de alavanca com relação ao ponto .
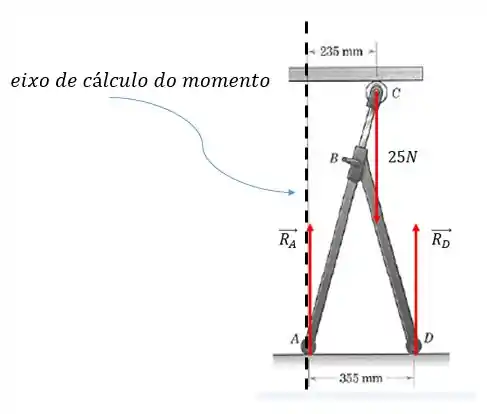
Perceba que a distância da força de até vale e a distância da força vale
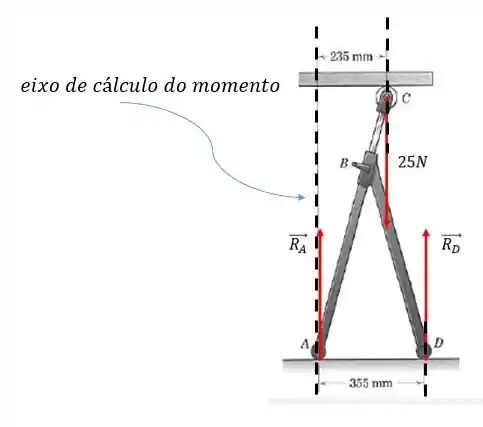
Adotando o sentido anti-horário como positivo, vamos ter que
Passo 3
Show de bola!
Agora, para achar vamos calcular momentos de novo?
Não!!! Vamos fazer uma coisa mais simples usando a outra condição:
Substituindo o valor de :
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/22
O centro de massa do carro de motor traseiro e com está localizado como mostrado na figura. Determine a força normal sob cada pneu quando o carro está em equilíbrio. Descreva qualquer hipótese feita.
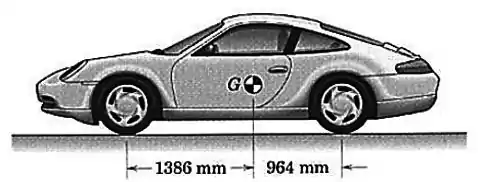
Passo 1
O sistema acima pode ser desenhado assim:
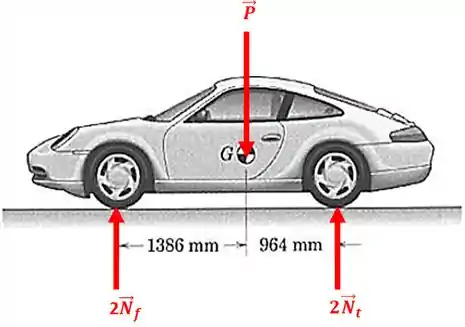
Onde, é a força peso, é a força normal na roda da frente e é a força normal na roda de trás.
Mas por que colocamos e Porque o carro tem quatro rodas e cada roda tem a sua força normal. Então, admitimos que o carro é simétrico e que a outra metade dele vai ter a mesma configuração de forças.
Passo 2
O carro possui , então o módulo da força peso será:
Agora vamos fazer o equilíbrio dessas forças:
Precisamos de outra equação para resolver o problema. Vamos fazer o somatório de momentos com relação ao ponto indicado na figura abaixo:
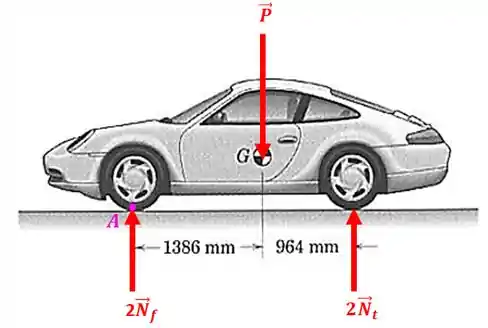
O equilíbrio de momentos em relação ao ponto nos dá:
Voltando para a equação do equilíbrio das forças, podemos substituir o valor de que achamos:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 96,3/6
A viga em uniforme e com sustenta a carga mostrada. Determine as reações nos apoios.
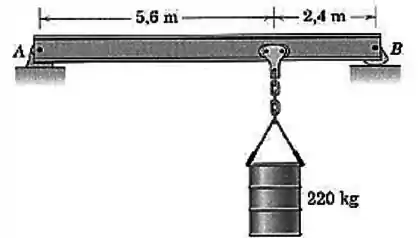
Passo 1
Nesse caso, temos que satisfazer a duas condições:
Perceba que a soma das forças horizontais tem que ser nula, já que a viga está presa:
E as forças têm a seguinte orientação:
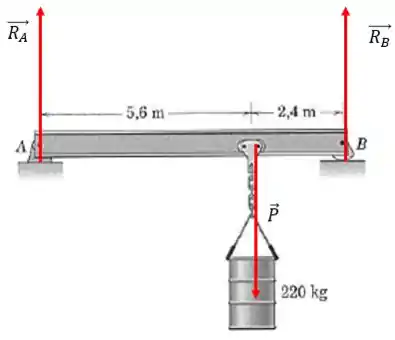
Certo? Não, faltou o peso da própria barra:
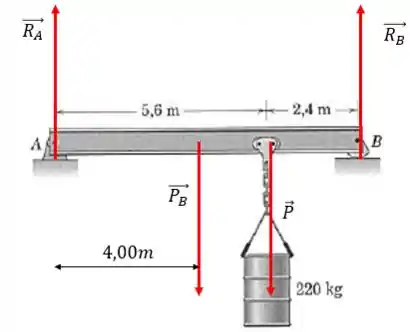
Passo 2
Vamos primeiro fazer o somatório de momentos usando o ponto como referência e considerando o sentido anti-horário como positivo:
Sendo que os pesos são:
Substituindo isso na nossa equação, vamos ter que:
Passo 3
Agora vamos para a segunda condição:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 120,3/97
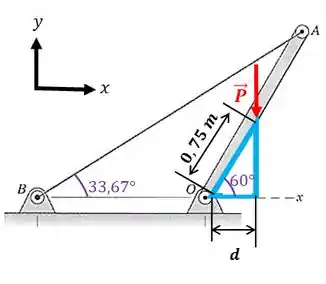
Calcule o módulo da força suportada pelo pino em no dispositivo em curva, carregado e apoiado como mostrado.
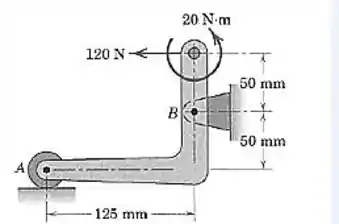
Passo 1
Aqui vamos ter que atender a três condições:
Passo 2
A forças de reação em e tem uma forma dada por:
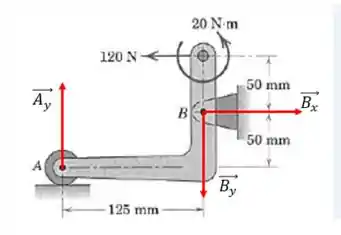
Perceba que a componente da reação em é nula. Isso se deve ao fato de que o apoio em é um apoio deslizante, ou seja, não há o impedimento desse apoio de se mover na horizontal. E não se esqueça: só colocamos reação de apoio na direção onde há impedimento do movimento.
Sendo assim, já descobrimos quanto vale
Passo 3
Agora vamos fazer o seguinte: calcular o equilíbrio de momentos em relação ao ponto
Vamos considerar o sentido anti-horário como o positivo:
Não pode esquecer de contabilizar o momento de que já tinha na estrutura.
Então, obtemos o seguinte:
Passo 4
Agora, usando o somatório de forças verticais:
Passo 5
Sendo assim, o módulo de será:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/7
Calcule as forças e o momento de reação na base aparafusada da estrutura de sinal de trânsito suspenso. Cada sinal tem uma massa de , enquanto que as massas dos elementos e são e , respectivamente.
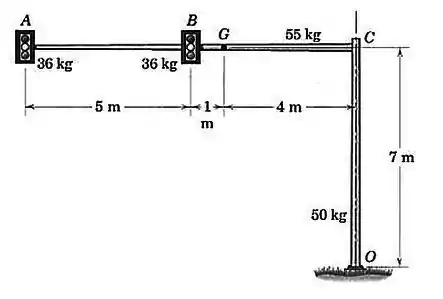
Passo 1
O diagrama de corpo livre pode ser representado por:
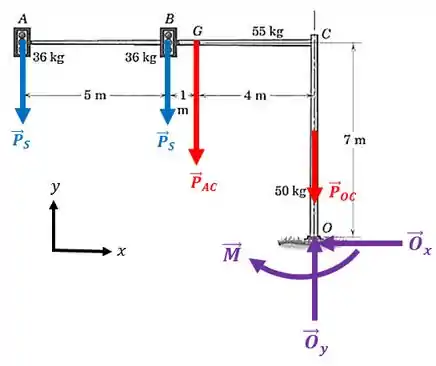
Passo 2
Vamos calcular as forças peso que estão no diagrama:
E vetorialmente, temos que a força peso do sinal aponta para baixo, então:
A força peso da barra é:
E o vetor é:
E por último o peso da barra :
Transformando em vetor temos:
Passo 3
Agora vamos achar as reações de apoio. Perceba que o apoio é um engaste, pois a estrutura não pode se movimentar em nenhuma direção e nem girar. Inclusive foi dito no enunciado que a base é aparafusada.
Vamos começar usando o equilíbrio de momentos em relação ao ponto e considerando o sentido de giro anti-horário como positivo, temos:
Repare que a força não tem braço de alavanca com relação ao ponto . Então, vamos substituir os valores:
Esse momento é positivo, ou seja, ele gira no sentido horário.
Passo 4
Perceba que não há forças horizontais além da reação de apoio , então:
Agora vamos fazer o equilíbrio das forças verticais:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 96,3/1
Determine a força necessária para manter o motor de na posição para a qual . O diâmetro em é desprezível.
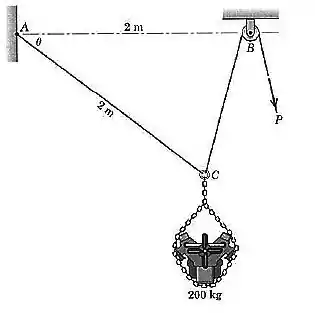
Passo 1
Se você reparar bem vai ver que esse é o caso em que as forças são concorrentes em um ponto só, ou seja, a linha de ação das forças passa por um dos ponto do desenho?
Você consegue identificar este ponto? É o ponto , dê uma olhadinha aqui:
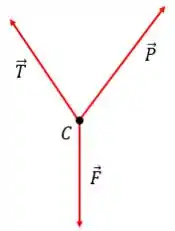
Esse é o nosso diagrama de corpo livre.
Perceba que, por se tratar de uma corda, a força pode ser representada ao longo de toda esta corda. Então, o que fizemos aqui foi transmitir a força e representá-la na direção .
Passo 2
Vamos usar um pouquinho de geometria agora: Perceba que esse é um triângulo que possui dois lados iguais. Assim, ele terá também dois ângulos iguais.
Perceba também que um dos três ângulos do triângulo vale . Sabendo que a soma dos ângulos dá , podemos escrever assim:
Assim:
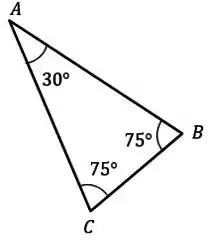
Passo 3
Então, colocando esses ângulos no nosso diagrama de corpo livre, temos isso aqui:
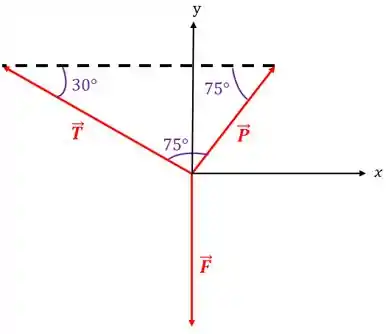
Agora, temos que decompor todas as forças nos eixos e para podermos fazer as somas dos vetores. Mas repare que temos que descobrir mais alguns ângulos para poder decompor esses vetores:
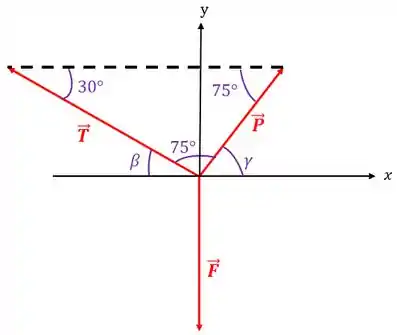
Repare que somando os ângulos e com obtemos :
Mas... Como vamos resolver essa equação se ela tem duas incógnitas? Temos que achar mais um ângulo antes. Para isso, vamos usar este triângulo aqui:
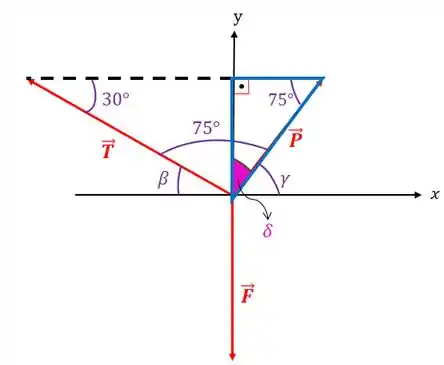
Vamos isolar esse triângulo que queremos para entendermos melhor o que precisamos fazer:
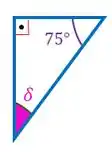
A soma de todos os ângulos internos de um triângulo deve dar , então:
Passo 4
Agora já conseguimos achar o ângulo :
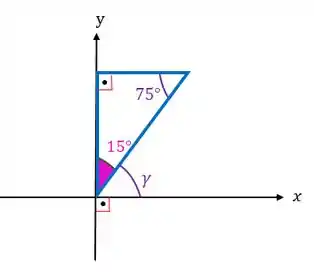
Repare que os eixos e são perpendiculares entre si, então:
Beleza?
Agora vamos resgatar aquela equação que não conseguimos resolver:
Passo 5
Pronto! Achamos todos os ângulos que eram necessários:
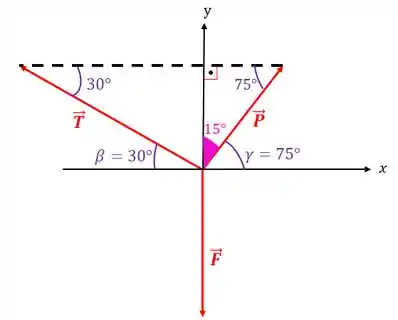
Então, vamos calcular o valor do módulo da força que é nada mais nada menos que o peso do motor:
Escrevendo esta força como um vetor, temos:
Agora vamos decompor a força e a força nos eixos e :
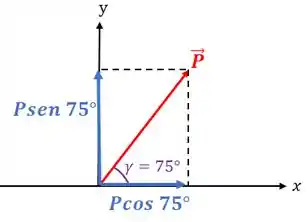
E a força fica assim:
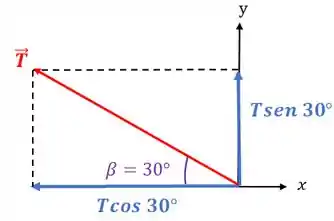
Passo 6
Vamos fazer agora o equilíbrio destas forças. Sabemos que a soma de todas as forças horizontais deve ser zero, então:
Vamos isolar a força para substituir na próxima equação:
Beleza?
Agora vamos fazer o equilíbrio das forças verticais:
Vamos substituir pela equação que achamos ali em cima:
Substituindo todos os valores de senos e cossenos, vamos ter que:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/7
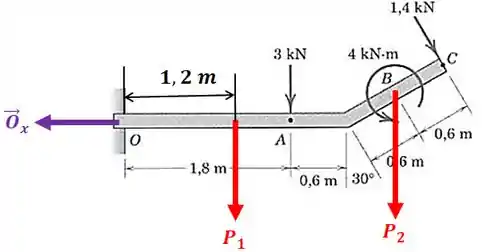
A viga uniforme tem massa de por metro de comprimento. Calcule as reações no apoio . As cargas mostradas estão em um plano vertical.
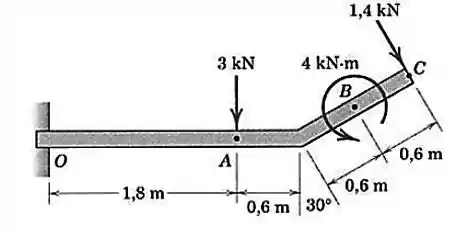
Passo 1
O diagrama de corpo livre pode ser representado por:
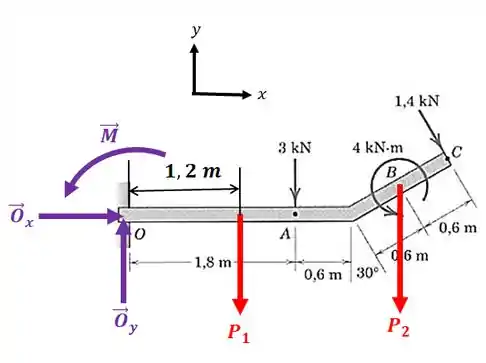
Perceba que o apoio é um engaste, então tem reações horizontal, vertical e o momento.
A força é o peso da barra horizontal e é o peso do trecho correspondente a barra inclinada.
Passo 2
Vamos calcular as forças peso das barras. Como a viga é uniforme e possui por metro de comprimento, a massa da barra horizontal é:
Então, o módulo de é:
Como todas as forças estão em , vamos passar o peso para esta unidade também:
Já a massa da barra inclinada é:
Então, o módulo de é:
Passando para a unidade de , temos que:
Beleza?
Passo 3
Vamos começar usando o equilíbrio de momentos em relação ao ponto :
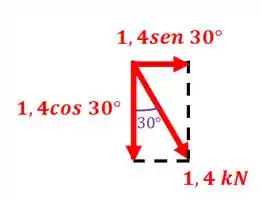
Mas antes vamos decompor aquela força inclinada de :
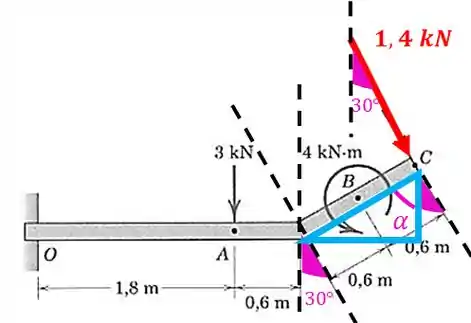
Como o ângulo de inclinação da força é de com relação à vertical, temos que:
Agora vamos usar o triângulo para achar as distâncias com relação ao ponto . Pelo desenho, temos que:
Se um dos ângulos internos de um triângulo retângulo é de , então o outro é :
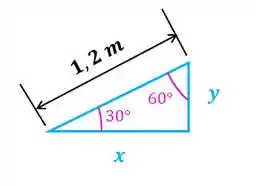
Portanto, o comprimento será:
Este valor será o braço de alavanca da componente horizontal da força de com relação ao ponto :
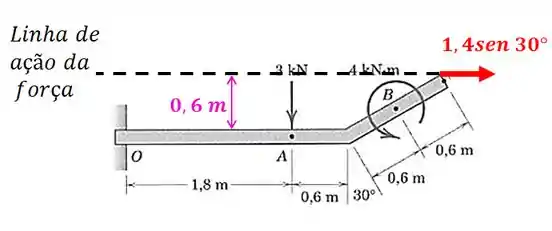
E o comprimento será:
Então, o braço de alavanca da componente vertical da força de com relação ao ponto é de:
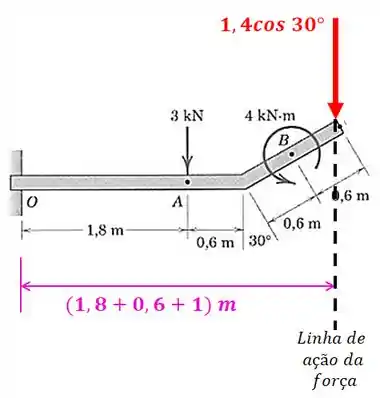
Passo 4
Agora sim podemos calcular o somatório de momento:
Repare que o braço de alavanca do peso da barra inclinada é igual a metade da altura do triângulo:
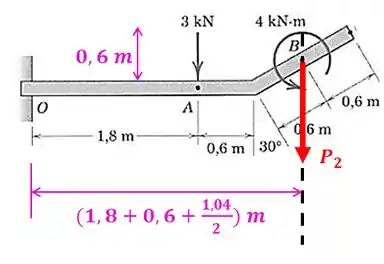
Então, a reação momento será de:
Como o momento deu positivo, indica que arbitramos um sentido correto para a reação de apoio, ou seja, o momento é no sentido anti-horário.
Passo 5
Agora vamos fazer o somatório de forças horizontais:
Repare que o sinal deu negativo, ou seja, arbitramos o sentido contrário para a reação . Dessa forma, esta força aponta para a esquerda (sentido contrário ao que desenhamos antes):
Passo 6
Agora vamos fazer o equilíbrio das forças verticais:
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/22
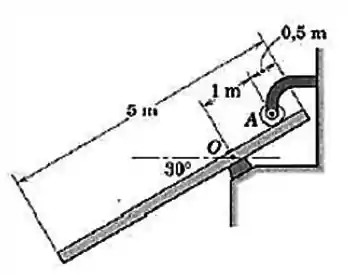
A barra uniforme de e massa de é articulada em e impedida de girar mais do que no plano vertical pelo rolete fixo em . Calcule o módulo da força total suportada pelo pino em .
Passo 1
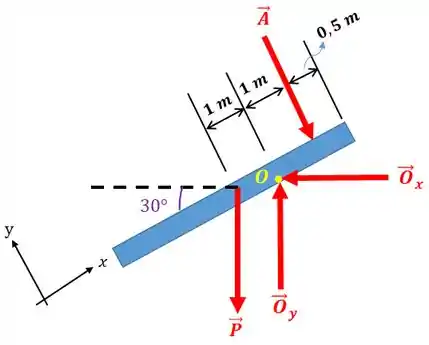
O diagrama de corpo livre pode ser representado por:
Passo 2
O módulo da força peso da barra vale:
Agora vamos decompor esta força no eixo :
Agora vamos usar o equilíbrio de momentos em relação ao ponto e considerando o sentido de giro anti-horário como positivo, temos:
Passo 3
Usando o equilíbrio de forças horizontais:
E o vertical:
Então, a resultante de forças no ponto é:
Resposta
Exercício Resolvido #9
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/22
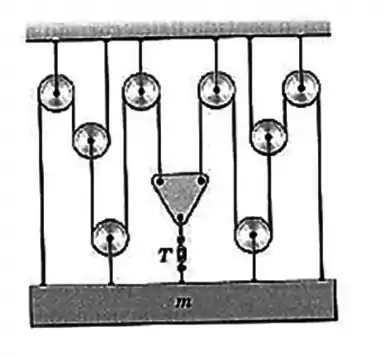
Determine a força trativa no parafuso tensor do sistema polia-cabo em termos da massa do corpo que ele sustenta. Despreze a massa das polias e do cabo.
Passo 1
Vamos olhar para o sistema de roldanas da esquerda:
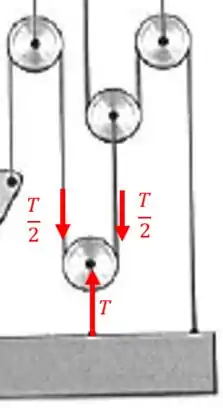
Cada roldana divide a tensão em . Assim, a segunda roldana vai gerar uma segunda divisão:
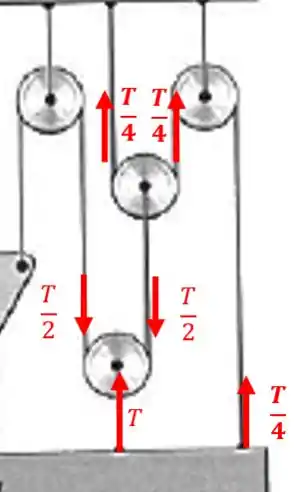
Passo 2
Assim, as forças do sistema vão ser assim:
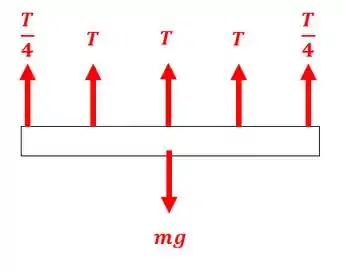
Assim, o equilíbrio de forças nos dá:
Resposta
Exercício Resolvido #10
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/22
Determine a força necessária para começar a rolar o cilindro uniforme de massa sobre o degrau
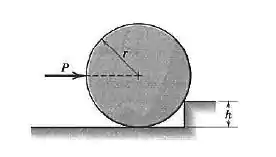
Passo 1
Bom, a primeira coisa que precisamos fazer é determinar quais são as forças que atuam no cilindro. São essas:
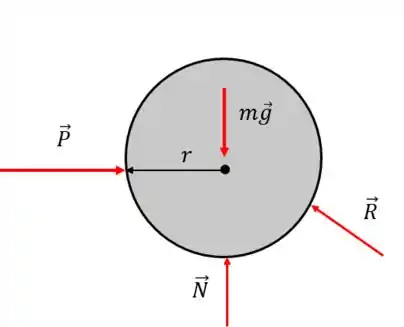
A força , que empurra o cilindro. A normal , devido ao contato do cilindro com o chão. E a reação , devido ao contato do cilindro com o degrau.
Passo 2
Beleza, mas nós queremos a força necessária para o cilindro subir. Isso quer dizer, em outras palavras, que a normal com o chão é nula: na iminência do giro, o cilindro perde o contato com o chão:
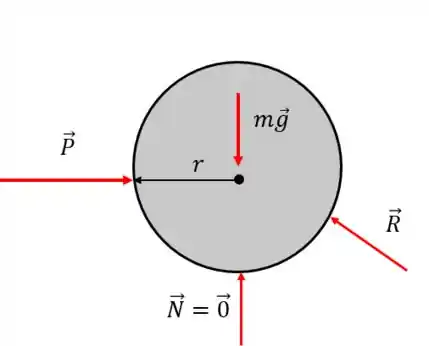
Bom, essa informação não vai ser tão relevante para achar o valor de , pelo menos não através do caminho que usaremos. Mas fica aí a informação teórica sobre isso.
Observação: estamos, é claro, procurando o valor do módulo de .
Passo 3
Bom, preste atenção no triângulo abaixo. Ele é formado pelas distâncias dadas na questão:
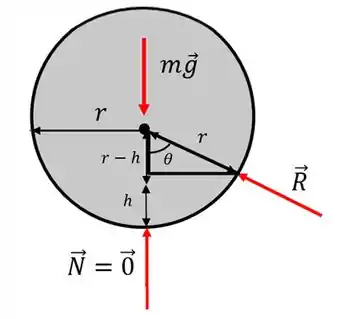
Vamos tirar este triângulo de dentro do outro desenho para facilitar a nossa visualização:
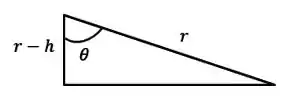
Passo 4
Vamos calcular o cosseno do ângulo que aparece no triângulo. Você entenderá nos próximos passos, quando formos decompor a força peso no cálculo do momento:
E, usando:
Sabemos que:
Então, vamos substituir isso na outra equação:
Desenvolvendo, chegamos a:
Passo 5
Agora vem o pulo do gato: vamos usar o equilíbrio de momentos para calcular o valor de
Na iminência de girar, o momento causado pela força compensa os momentos das outras forças.
Tomando o ponto de contato do cilindro com o degrau como referência, teremos as seguintes forças exercendo o momento: o peso e a força
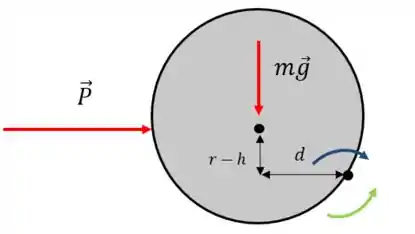
Assim:
Sacou?
Bom, e quanto vale
Passo 6
Agora sim vamos usar o nosso triângulo:
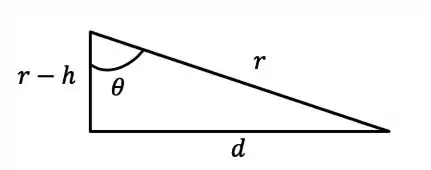
Sacou? é dado por:
E quanto vale
Assim:
Assim, voltando ao cálculo dos momentos:
Pronto!
Resposta
Exercício Resolvido #11
R.C. Hibbeler, Mecânica para engenharia, Estática, 12° ed. SP: Pearson Prentice Hall, 2011, 171, 5/41
Determine as componentes horizontal e vertical da reação no pino e a reação do colar liso sobre a barra.
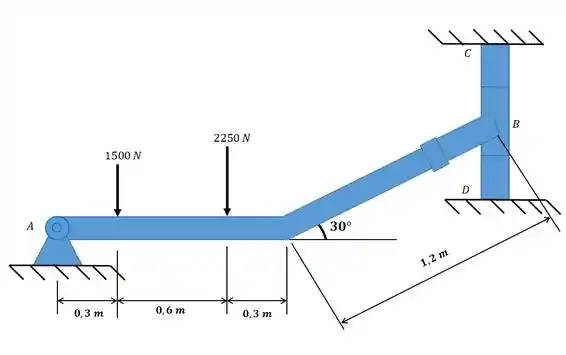
Passo 1
O diagrama de corpo livre dessa estrutura fica assim:
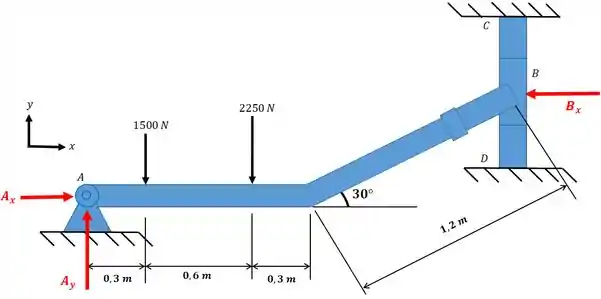
Perceba que o apoio impede o movimento somente na horizontal, por isso tem uma reação de apoio. Já o apoio em impede o movimento tanto na horizontal quanto na vertical.
Passo 2
Para achar as reações, temos que começar fazendo o somatório de momentos com relação a um ponto. Mas qual ponto vamos escolher?
Vamos escolher o ponto .
Passo 3
Vamos achar a distância da reação até o ponto :
Então:
Passo 4
Agora vamos fazer o somatório de momentos com relação ao ponto considerando o sentido anti-horário como positivo:
Passo 5
Agora vamos fazer o somatório de forças horizontais:
Passo 6
Para finalizar vamos fazer o equilíbrio das forças verticais:
Resposta
Exercício Resolvido #12
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/29
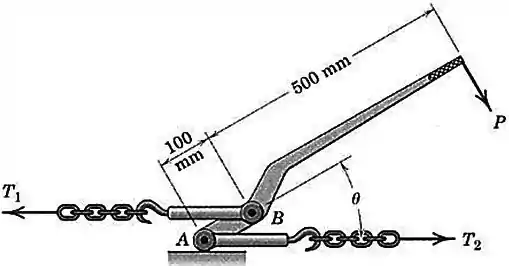
O conector de correntes é utilizado para segurar cargas de troncos, madeira, tubos e congêneres. Se a força trativa vale quando , determine a força necessária na alavanca e a força trativa correspondente para essa posição. Admita que a superfície sob é perfeitamente lisa.
Passo 1
O diagrama de corpo livre fica assim:
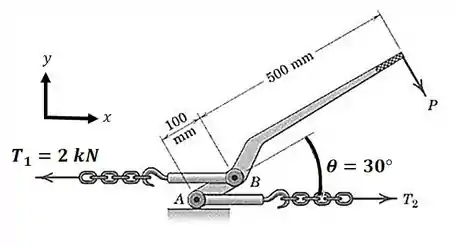
Passo 2
Repare que pelo ponto passa a linha de ação da força trativa , então essa força não exerce momento neste ponto.
Então, vamos começar calculando o momento com relação ao ponto para podermos achar o valor de :
Mas antes vamos achar as distâncias das forças até o ponto .
Passo 3
Vamos começar achando a distância da força com relação ao ponto . Mas repare que a força está inclinada... Então, temos que achar a distância de cada uma de suas componentes com relação ao ponto .
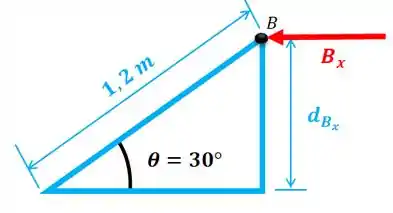
Temos que a distância é:
E para a componente , temos:
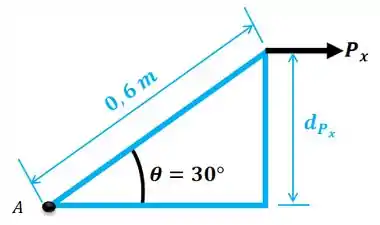
Passo 4
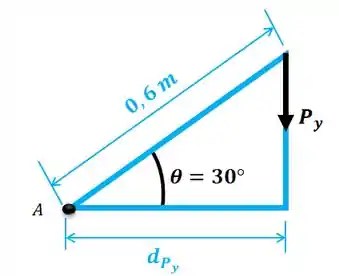
Agora vamos achar a distância da força com relação ao ponto . Para isso, vamos usar este triângulo aqui:
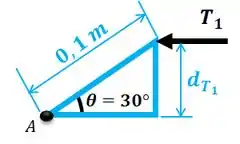
Passo 5
Agora vamos decompor a força :
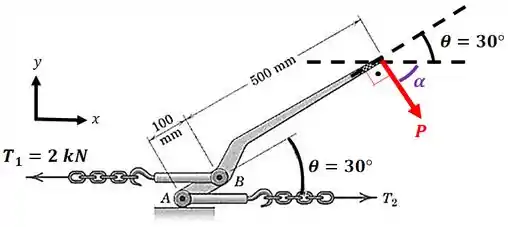
Vamos achar o ângulo que a força faz com relação a horizontal. Repare que a soma dos ângulos deve dar , então:
Agora sim podemos achar as componentes da força :
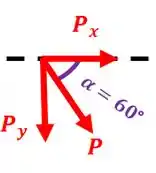
Então:
E:
Passo 6
Agora sim podemos calcular o somatório de momento com relação ao ponto . Para isso vamos considerar o momento positivo no sentido anti-horário:
Passando isso para Newton, temos:
Passo 7
Agora vamos fazer o somatório de forças horizontais:
Repare que estamos usando todas as forças na mesma unidade que é Newton!
Então:
Resposta
Exercício Resolvido #13
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/54
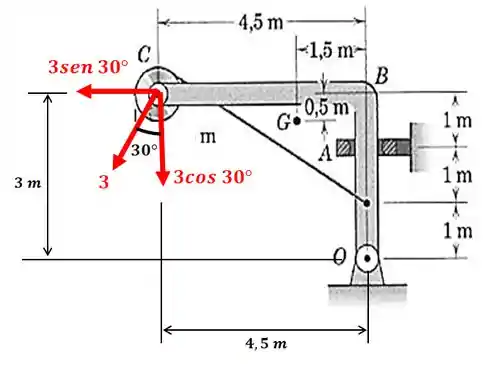
O elemento e a roldana em , juntos, têm uma massa de , com um centro de massa combinado em . Calcule o módulo da força suportada pela conexão de pino em quando a carga de é aplicada. O colar em só pode dar apoio na direção horizontal.
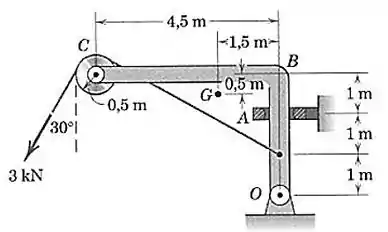
Passo 1
O diagrama de corpo livre desta estrutura fica assim:
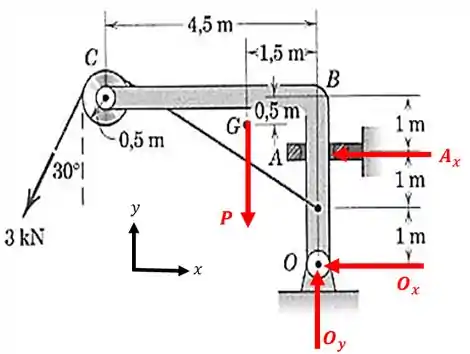
Repare que o colar em só impede o movimento na direção horizontal, então colocamos uma reação horizontal neste ponto.
Já o apoio em impede os movimentos horizontal e vertical, por isso colocamos duas reações sendo uma em cada direção.
Passo 2
Vamos começar fazendo o somatório de momentos com relação ao ponto , porque assim conseguimos achar o valor da reação :
Mas repare que temos uma força inclinada de ... Vamos levar esta força para o centro da roldana. Mas quando levamos a força, sempre temos que levar o momento que ela faz com relação ao ponto:
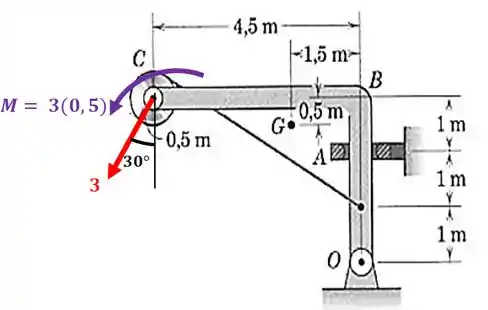
Esse momento surgiu devido ao braço de alavanca com relação ao centro da roldana ser de , assim:
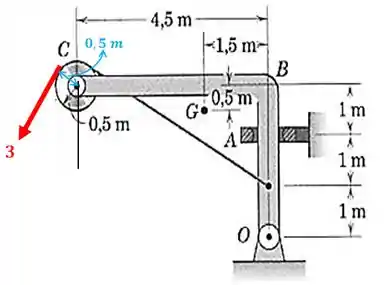
Beleza?
Agora sim podemos achar as componentes vertical e horizontal da força de :
Passo 3
Vamos achar o módulo da força peso:
Passando tudo para a mesma unidade:
Então, temos:
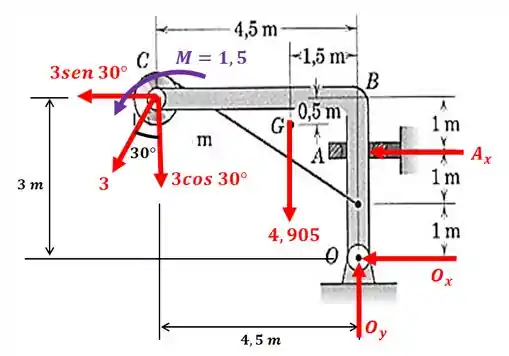
Agora sim podemos calcular o momento, considerando o sentido anti-horário como positivo:
Repare que achamos uma força com sinal negativo, isso porque arbitramos o sentido contrário para a reação no diagrama de corpo livre. Na verdade, deve ser assim:
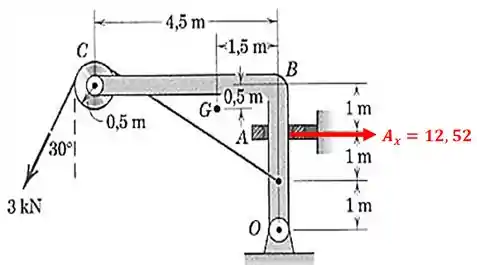
Passo 4
Agora vamos fazer o somatório de forças horizontais:
Passo 5
E para finalizar vamos fazer o somatório de forças verticais:
Passo 6
Vamos calcular a resultante das forças no ponto :
Resposta
Exercício Resolvido #14
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/37
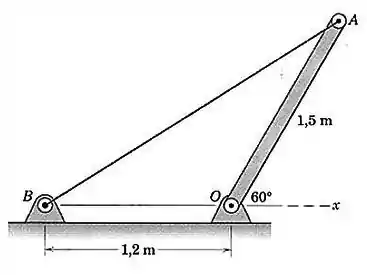
A barra uniforme com é mantida na posição mostrada por um pino liso em e pelo cabo . Determine a força trativa no cabo e o módulo e a direção da reação externa no pino em .
Passo 1
O diagrama de corpo livre dessa estrutura é:
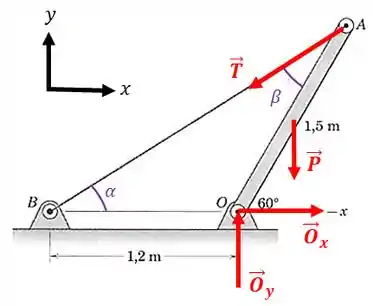
Passo 2
Para achar as reações, temos que começar fazendo o somatório de momentos com relação a um ponto. Mas qual ponto vamos escolher?
Aquele que tenha alguma das nossas incógnitas. Dessa forma, eliminamos alguma das incógnitas, já que a força que está bem em cima do ponto que escolhermos não possui braço de alavanca.
Vamos escolher o ponto .
Mas antes temos que calcular as distâncias das forças até o ponto .
Passo 3
Vamos começar achando os ângulos e . Para isso, vamos formar o seguinte triângulo retângulo:
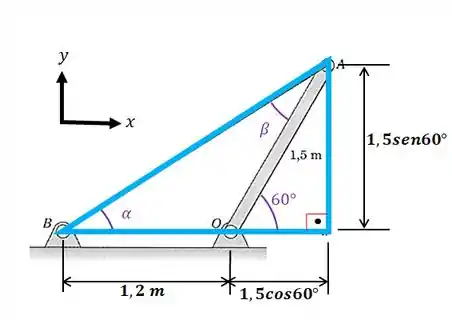
Temos que o ângulo é:
Passo 4
Sabendo o ângulo podemos decompor a força trativa :
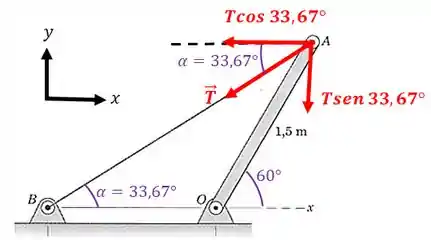
E as distâncias de cada componente com relação ao ponto são:
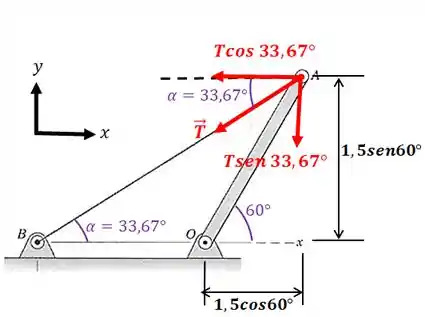
Passo 5
Agora vamos achar a força peso:
E a distância dela até o ponto ? Vamos fazer o seguinte triângulo retângulo:
Repare que a força está posicionada na metade da barra de , ou seja, está a . Então, a distância é:
Passo 6
Agora sim podemos calcular o somatório de momento com relação ao ponto . Para isso vamos considerar o momento positivo no sentido anti-horário:
Passo 7
Agora vamos fazer o somatório de forças horizontais:
Repare que o sinal deu positivo. Isso significa que arbitramos o sentido da reação certinho.
Passo 8
Agora vamos fazer o equilíbrio das forças verticais:
Passo 9
Agora temos que achar a resultante no apoio :
Agora temos que saber o ângulo que a resultante faz com relação ao eixo :
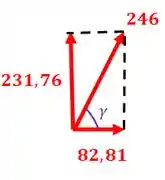
Resposta
Exercício Resolvido #15
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 99, 3/53
Determine as reações externas em e para a treliça de um telhado carregada como mostrado. As cargas verticais representam o efeito de sustentação dos materiais do telhado, enquanto a força de representa uma carga devida ao vento.
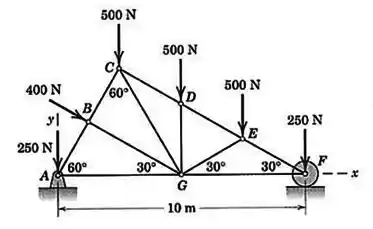
Passo 1
O diagrama de corpo livre dessa treliça fica assim:
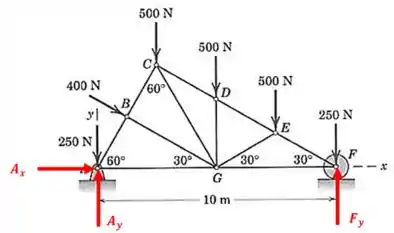
Perceba que o apoio impede o movimento tanto na vertical quanto na horizontal, por isso tem duas reações de apoio. Já o apoio em é um rolete, ou seja, permite que a estrutura se mova na horizontal, mas impede o movimento na vertical.
E não esqueça que só colocamos reação de apoio na direção em que há o impedimento de movimento.
Passo 2
Para achar as reações, temos que começar fazendo o somatório de momentos com relação a um ponto. Mas qual ponto vamos escolher?
Temos que escolher um ponto que tenha uma das nossas incógnitas, ou seja, o ponto ou . Dessa forma, eliminamos uma das incógnitas, já que a força que está bem em cima do ponto que escolhermos não possui braço de alavanca.
Vamos escolher o ponto .
Repare que não temos as distâncias da maioria das forças... Então, vamos achar!
Passo 3
Vamos começar separando os triângulos que formam a treliça e achando seus ângulos. Vamos começar por este aqui:
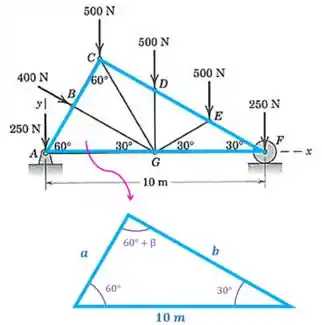
A gente sabe que a soma de todos os ângulos internos de um triângulo é igual a , então o ângulo será:
Então, temos o seguinte triângulo:
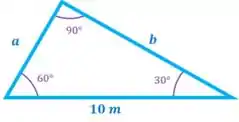
Vamos usar a lei dos senos para achar o valor do lado :
Como o triângulo é retângulo, pois tem um ângulo de , vamos usar o Teorema de Pitágoras para achar o lado :
Vamos passar para outro triângulo.
Passo 4
Agora vamos pegar esse triângulo aqui:
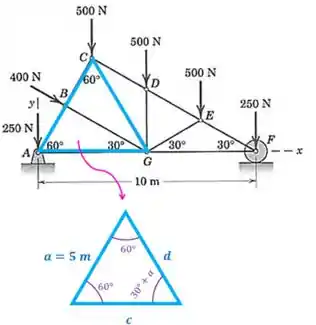
O ângulo será:
Como este triângulo tem todos os ângulos iguais a ele é um triângulo equilátero. Lembra deste triângulo? Ele tem todos os lados iguais. Ou seja, todos os lados do nosso triângulo serão iguais a :
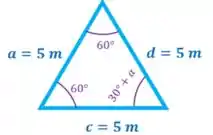
Passo 5
Agora vamos achar a distância das forças com relação ao ponto que ainda não sabemos:
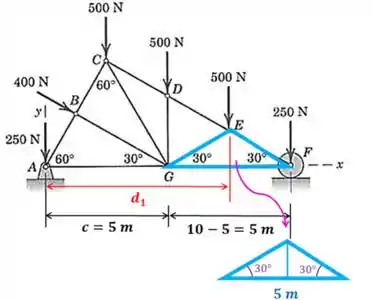
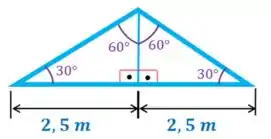
Para achar a distância vamos usar o triângulo destacado na figura. Precisamos saber quanto vale metade da sua base. Mas repare que esse triângulo é isósceles, pois tem os dois ângulos iguais. Você lembra o que é triângulo isósceles? É aquele que tem dois lados iguais.
Então:
Agora conseguimos achar a distância :
Beleza?
Passo 6
Vamos a achar a distância agora:
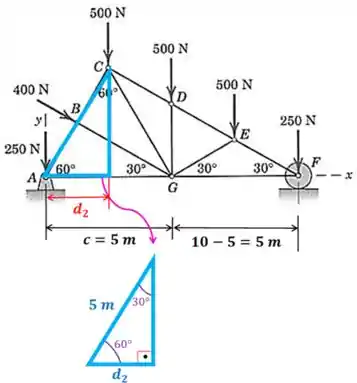
Vamos usar trigonometria para achar a distância :
Passo 7
Agora só falta achar a distância da força de . Mas repare que esta força está inclinada, então vamos começar decompondo-a:
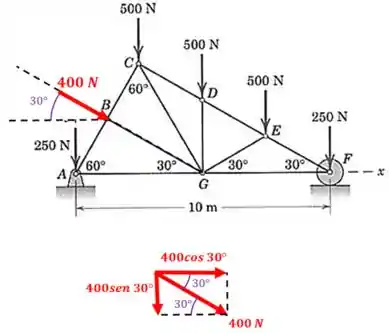
Agora vamos achar as distâncias dessas duas componentes até o ponto :
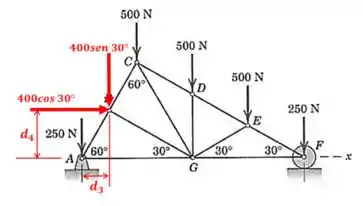
Para isso, vamos começar usando semelhança de triângulos com dois triângulos que tem ângulos internos iguais, são eles:
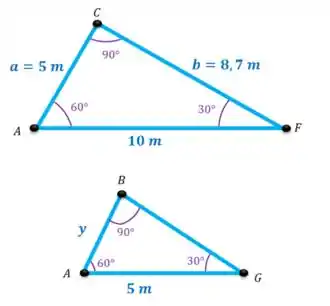
Então:
Agora conseguimos achar as distâncias e :
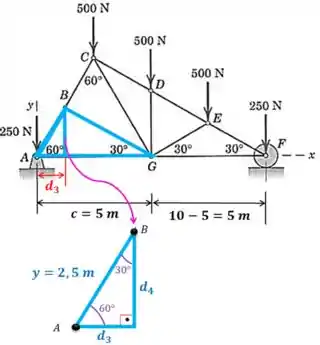
Vamos usar trigonometria para achar :
Agora vamos achar :
Pronto, temos todas as distâncias!!!!
Passo 8
Agora sim podemos calcular o somatório de momento com relação ao ponto . Para isso vamos considerar o momento positivo no sentido anti-horário:
Passo 9
Agora vamos fazer o somatório de forças horizontais:
Repare que o sinal deu negativo. Isso significa que arbitramos o sentido da reação ao contrário no diagrama de corpo livre. Ou seja, está apontando para o sentido negativo do eixo .
Passo 10
Agora vamos fazer o equilíbrio das forças verticais: