Equilíbrio em Três Dimensões
Produzido por Pablo RicardoTeoria
Introdução
Aqui vamos expandir nossos horizontes para o universo das três dimensões.
Imagine aquela mesma tábua do tópico anterior agora apoiada em um tijolo... E você coloca sobre ela vários pesos de massas diferentes. Como fica o equilíbrio agora?

Ahhh mas a tábua tem três dimensões! E agora?
Perceba que vamos ver situações mais próximas da realidade, já que vivemos em um mundo tridimensional.
Então, fica calmo e vem comigo aprender como resolver isso! Partiu?
Tipos de equilíbrio
- Forças Concorrentes em um ponto
- Forças concorrentes em uma linha:
- Forças Paralelas:
- Caso Geral:
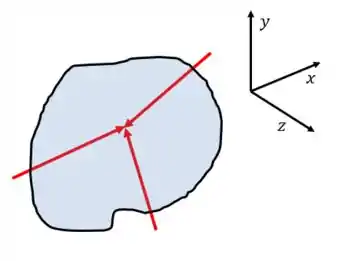
Nesse caso, semelhante ao que vimos no tópico , as condições de equilíbrio serão:
Viu a diferença? Agora temos uma equação a mais para as componentes das forças na direção
Para calcular essas paradas você já sabe: basta decompor as forças em cada um dos eixos e soma-las respeitando seu sentido positivo ou negativo.
E como todas as forças apontam para um mesmo ponto, o momento é nulo.
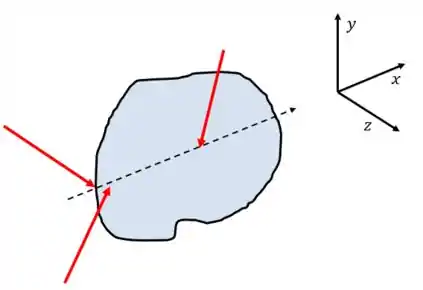
Nesse caso, existirá o momento, mas não em relação ao eixo definido pela linha. No desenho do exemplo, a linha é paralela ao . Assim, as condições de equilíbrio serão:
Lembra que se uma força cruzar um eixo ela não realiza momento em relação a esse eixo? É por isso que não existe momento em relação ao eixo , pois a linha do desenho é paralela a este eixo.
Ou seja, só haverá momento nos eixos em que as forças não estão chegando.
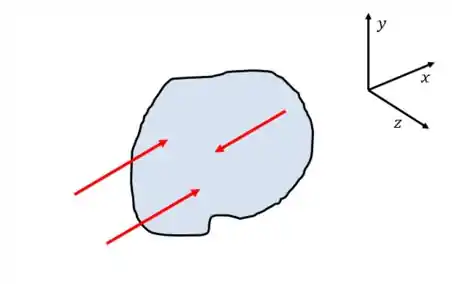
Da mesma forma que nos outros casos, teremos:
E o momento? Bom, perceba que se as forças forem paralelas a um eixo, não realizarão momentos em relação a ele. Assim, de acordo com o desenho do exemplo, só haverá momento nos eixos e :
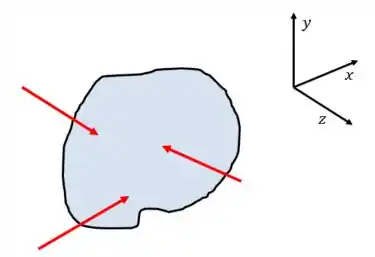
E, como sempre, sabemos que no caso geral as condições abrangem todos os eixos tanto para as forças quanto para os momentos:
Show de bola?
#PartiuExercitar
Tipos de equilíbrio
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 112, 3/62
Uma chapa quadrada e uniforme de aço de de comprimento de aresta e uma massa de está suspensa no plano horizontal pelos três fios verticais, como mostrado. Calcule a força trativa de cada fio.
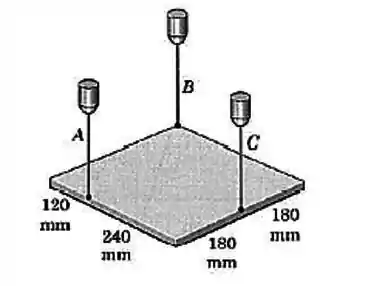
Passo 1
Vamos desenhar o sistema junto com os eixos:
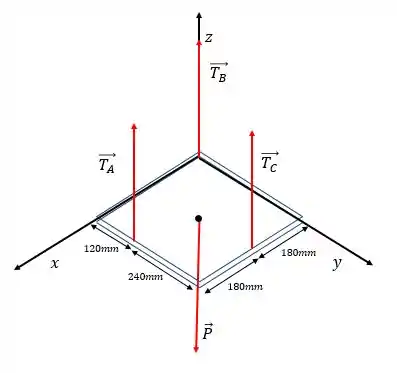
Para que a placa esteja em equilíbrio, as seguintes relações precisam ser satisfeitas:
Passo 2
Vamos primeiro calcular os momentos em relação ao eixo
Para isso, perceba que e tendem a girar a placa em torno do eixo no mesmo sentido; já o peso, tende a girar a placa no sentido contrário. Além disso, perceba que está a uma distância de do eixo , a uma distância de e a uma distância de
Sendo, o módulo da força peso da placa igual a:
Então, os momentos de cada uma das forças com relação ao eixo é::
Como todos os termos estão multiplicados por , podemos cortar ele da equação:
Dividindo tudo por
E perceba que não realiza momento, pois ele está bem em cima do eixo e não tem braço de alavanca com relação a este eixo.
Passo 3
Agora vamos para o eixo
Aqui as forças e continuam exercendo momento de sentidos iguais assim como o momento do peso continua se opondo a eles. O que mudou foi a distância das forças:
está a uma distância de do eixo , e está a uma distância de do eixo. tem uma distância de do eixo:
Cortando todos os
Passo 4
Já temos esse sistema aqui:
Podemos subtrair a primeira equação da segunda:
Substituindo essa relação na segunda equação:
E será:
Passo 5
Agora, para achar , basta a agente usar a relação do equilíbrio das forças:
Assim:
Resposta
Exercício Resolvido #2
J.L. Meriam& L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 112, 3/63
O eixo horizontal de aço tem uma massa de e está suspenso por um cabo vertical em e por um segundo cabo que passa por baixo do eixo e está situada em um plano vertical transversal. Calcule as forças trativas e nos cabos.
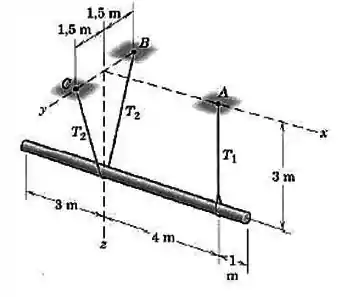
Passo 1
Para que o sistema esteja em equilíbrio, as duas condições abaixo precisam ser satisfeitas:
A configuração das forças é mais ou menos assim:
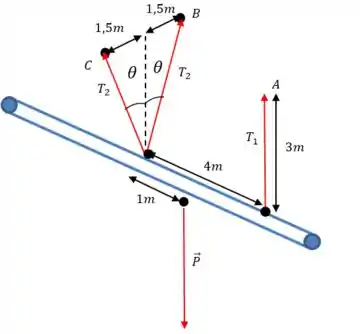
Pela figura do enunciado dá para notar que a barra tem de comprimento. Sendo assim, o peso é aplicado no centro da barra, numa distância de de cada extremidade.
Ainda pela figura do enunciado, vemos que as forças de valor são aplicadas a uma distância de da extremidade. Sendo assim, o peso será aplicado a uma distância de do ponto de aplicação das forças.
Passo 2
Vamos calcular os momentos das forças em relação ao eixo que passa em .
Nesse caso, perceba que as duas forças de valor não exercem momento em relação a esse eixo.
Só o peso e a exercem.
Vamos calcular o módulo do peso da barra:
Perceba que essas forças geram momentos de sentidos contrários. Assim:
Passo 3
Agora ficou mais fácil, vamos usar a segunda condição para achar .
Antes disso, veja que a gente tem que pegar apenas a componente vertical da força ():
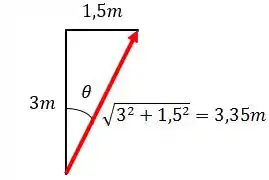
Ou seja:
Passo 4
Bom, mas são duas forças, então:
Observando o nosso triângulo, vemos que o cosseno do ângulo é:
Substituindo isso na equação de , temos que:
Assim:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 112, 3/65
A parte de um lustre que é sustentada por correntes tem a forma de uma parte de casca esférica. Se a massa da parte de vidro é , determine a força trativa em cada uma da correntes.
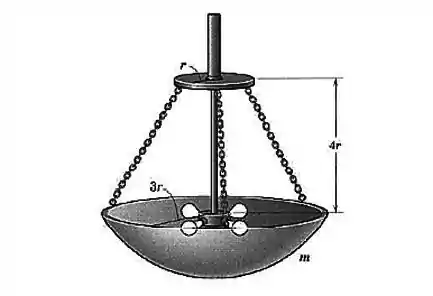
Passo 1
Bom, quais são as forças que agem no sistema?
A força peso e a força de tensão em cada uma das correntes.
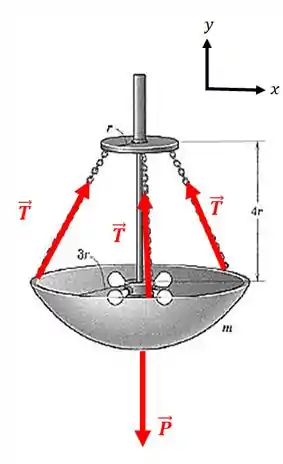
Para que a massa esteja em equilíbrio, vamos precisar garantir que:
Passo 2
O sistema simplificado pode ser representado assim:
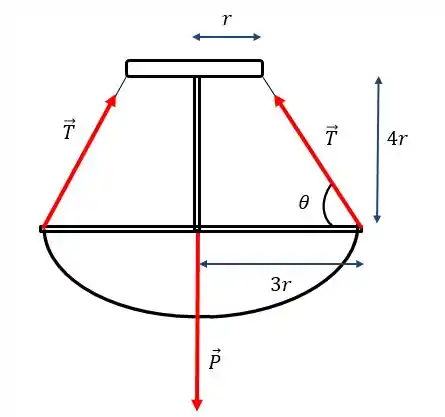
Passo 3
Bom, pelo desenho e pelo enunciado, percebemos que as componentes verticais das tensões () vão equilibrar o peso. Assim, podemos escrever:
Lembre-se: são três correntes igualmente espaçadas, sendo assim, são três tensões.
Passo 4
Pelo triângulo formado pela tensão, podemos dizer:
Nós só não sabemos quem é mas basta usarmos o triângulo retângulo da figura:
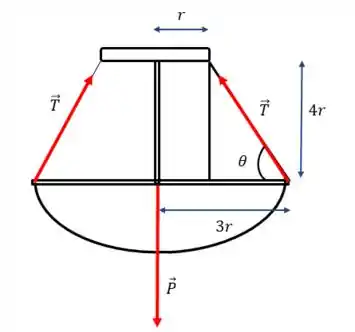
Pra ficar mais fácil de ver, vamos tirar o triângulo do desenho:
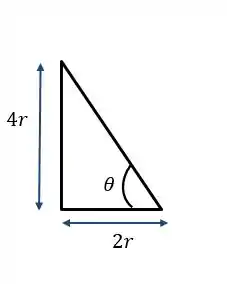
Assim:
Passo 5
Então:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 113, 3/69
Uma banqueta de três pernas está submetida à carga , como mostrado. Determine a força de reação vertical sob cada perna. Despreze o peso da banqueta.
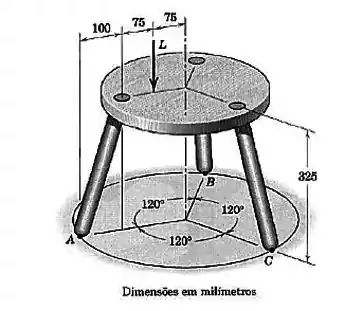
Passo 1
O que queremos saber nessa questão é quais são os módulos das forças de reação: e.
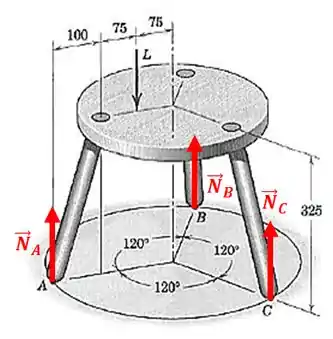
Em primeiro lugar, veja que as forças de reação em e serão iguais. Por quê? Porque existe um plano de simetria passando entre e
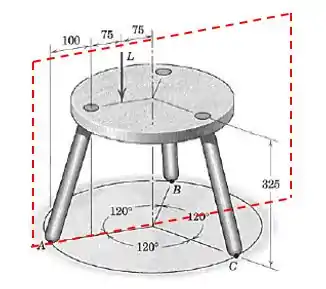
Esse plano divide a figura em duas partes iguais. Faz sentido pensar que tudo que ocorrer fisicamente em uma metade ocorrerá na outra também, não é mesmo?
Passo 2
Agora vamos testar o equilíbrio de momentos em relação ao eixo
Mas vamos ser espertos: passaremos o eixo em cima do ponto Dessa forma, o momento que realizar será nulo em relação a esse eixo:
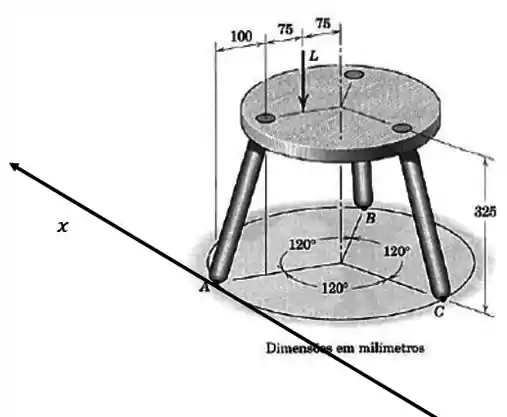
Passo 3
Beleza! Agora só precisou calcular o momento que cada força faz em relação a esse eixo.
Assim de cara, perceba que as forças de reação apontarão na direção contrária à força .
Além disso, veja que a direção horizontal da força até o eixo é de:
.
Assim, podemos dizer que o momento da força é dado por:
Vamos atribuir a este momento o valor positivo. E o valor negativo ao momento das outras forças.
Passo 4
Bom, vamos às outras forças. Em primeiro lugar, pela simetria, como vimos, elas serão iguais:
E qual será a distância das forças até o eixo?
Temos que usar um pouco de trigonometria:
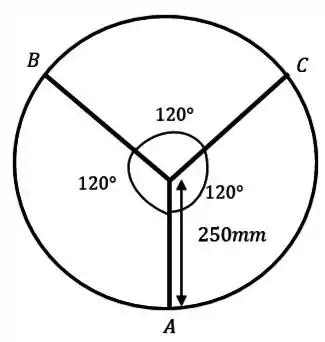
Essa é a vista de cima da projeção do banco no chão.
Qual é a distância de até
Basta a gente formar o triângulo abaixo em cima da figura:
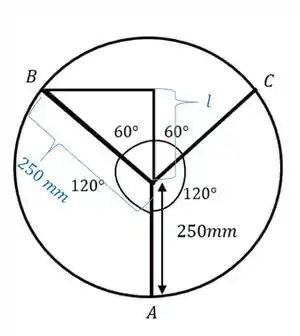
Em outras palavras, a distância vai ser igual a mais o lado () do triângulo acima. Podemos calcular o lado usando trigonometria:
Então, a distância total do ponto até o ponto é:
E a distância de até Mesma coisa, já que é simétrico:
Passo 5
Beleza, então os momentos de cada força valerão:
Usando a relação:
Simplificando e isolando essa parada:
Passo 6
Beleza, mas falta achar . Agora ficou fácil: Bata a gente usar o equilíbrio das forças:
Perceba que a forças normais apontam em um sentido contrário ao da força Assim:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 113, 3/80
Durante um teste, o motor esquerdo do avião bimotor é acionado gerando um empuxo de . As rodas principais em e estão freadas de modo a evitar movimento. Determine a variação nas forças de reação normais e (comparativamente aos valores nominais com ambos os motores desligados).
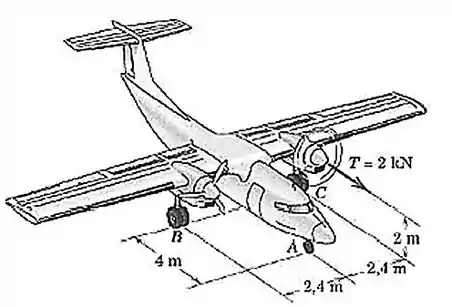
Passo 1
A ideia é a seguinte: com os dois motores ligados, havia um grupo de reações que atingiam o avião.
Com apenas uma turbina ligada, essas forças sofrem uma variação. Não queremos achar essas novas forças, mas sim a variação delas. Então, estamos procurando:
Sendo essas as variações das forças normais.
Passo 2
Vamos traçar um eixo que passe por e
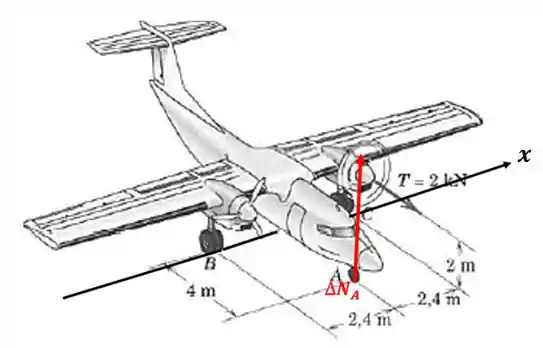
Nesse primeiro momento, queremos descobrir o valor de Desenhando sem o avião e apenas com as forças que nos interessam:
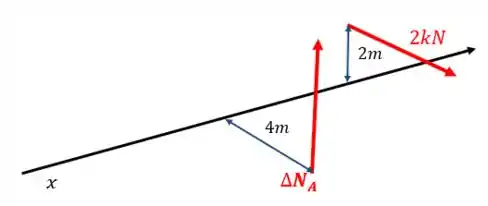
Perceba que elas vão realizar momentos de sentidos contrários.
E qual foi o motivo de não termos usado as outras forças até esse ponto? Bom, porque o eixo passa em cima de e, pontos de aplicação de todas as outras forças. Sendo assim, os momentos delas são nulos ali.
Voltando aos cálculos:
Passo 3
Agora vamos passar um eixo que cruze o ponto
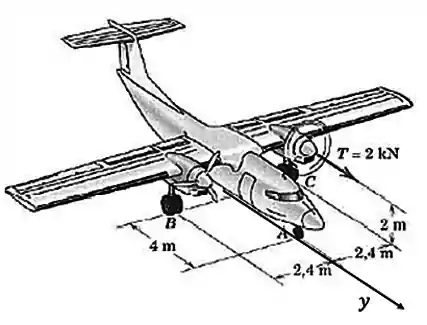
Desenhando sem o avião:
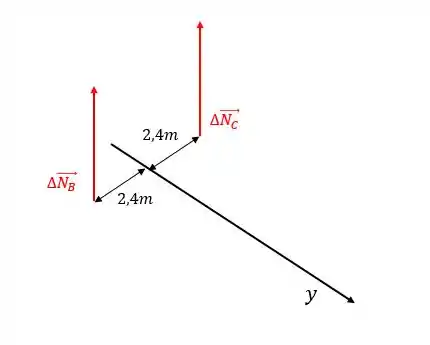
Dá pra perceber que os momentos terão sinais contrários, né? Assim:
Bom, vamos usar essa informa��ão a seguir.
Passo 4
Aí vem uma sacada importante: o que você diria que é o resultado da soma das variações das forças verticais?
Bem, para que o avião fique em equilíbrio, temos que ter:
Ou seja, a soma das forças verticais precisa ser nula. Isso precisa ser respeitado em qualquer condição, mesmo que haja variações.
Sendo assim, a soma das variações das forças precisa ser nula também:
Juntando o que vimos antes:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 113, 3/84
A mola de módulo é esticada de uma distância quando o mecanismo está na posição mostrada. Calcule a força necessária para iniciar rotação em torno do eixo e determine os módulos correspondentes das forças nos mancais, as quais são perpendiculares à . Qual é a força de reação normal em se ?
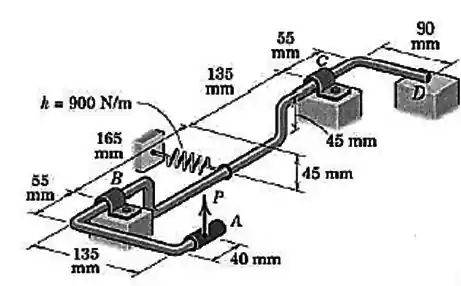
Passo 1
O desenho abaixo pode exemplificar o sistema:
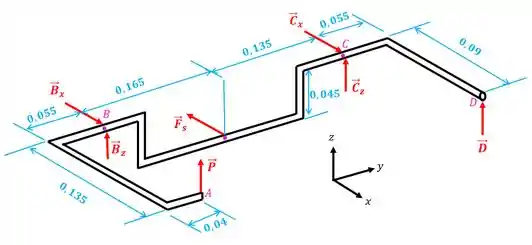
Perceba que é a força elástica.
Passo 2
O módulo da força elástica é dado por:
Na situação de rotação, a reação vai ser nula: Para esse caso, vamos calcular as reações:
Com relação ao eixo :
E:
Passo 3
Pelo equilíbrio de forças:
E no eixo :
Assim, os módulos serão:
Passo 4
Para o caso em que :
Assim, nesse caso, a força será:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 113, 3/113
A estrutura é usada para armazenar e desenrolar cabos. A massa combinada da estrutura, do corretel e do cabo é de com centro de massa em . Determine as forças normais nos quatro pés e ) se o cabo sai pela parte de cima do carretel e o cabo sai pela parte de baixo do carretel em seu ponto médio horizontal. O raio efetivo do carretel é de .
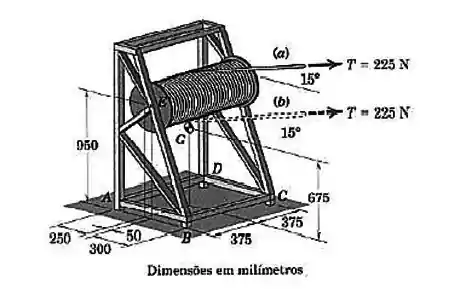
Passo 1
a)
Visto de lado, o negócio fica assim:
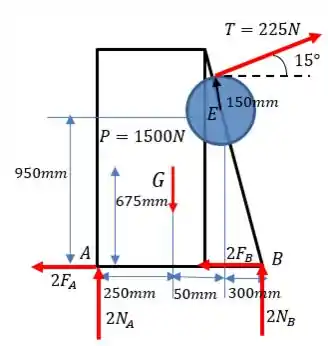
Já que a tensão sempre é aplicada no ponto médio, temos uma simetria que garante que:
E:
Por isso temos e .
Primeiro vamos calcular o binário da força de em relação ao ponto e representar a força de no ponto (o centro do círculo):
Vamos aplicar o equilíbrio de momentos no ponto
Assim:
Agora vamos usar o somatório de forças:
Assim:
Passo 2
b):
E no caso de a força estar assim?
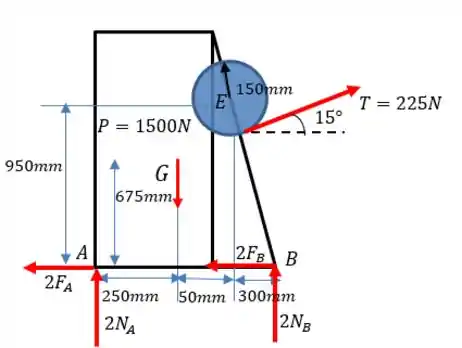
O que vai mudar nesse caso? Apenas o sinal do binário do Assim:
Assim:
Aplicando o equilíbrio de forças:
Assim:
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 115, 3/112
O mastro de , com centro de massa em , é mantido na posição mostrada por uma rótula em e por dois cabos e . Determine as forças trativas nos dois cabos e as componentes , e da força de reação em .
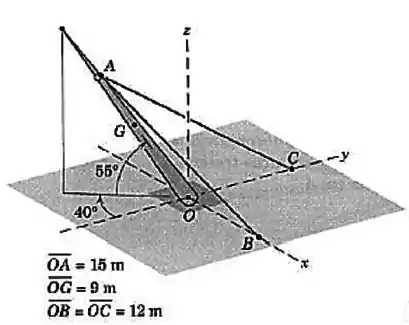
Passo 1
O sistema acima pode ser representado pelo desenho abaixo:
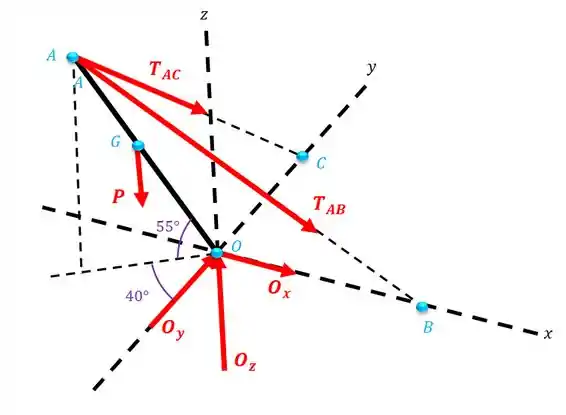
Passo 2
Vamos escrever cada uma das forças na forma vetorial:
Coordenadas do ponto :
Temos uma coordenada no eixo
Pra achar as coordenadas , basta projetar na horizontal e depois projetar em cada um dos eixos, e
Assim:
E as coordenadas do centro de gravidade (onde o peso é aplicado)?
Assim:
As coordenadas de são:
E de
Passo 3
Assim:
Então:
E:
O peso é dado por:
E ainda temos as forças de reação em
Passo 4
Vamos aplicar as equações de equilíbrio de forças:
Percebam que temos 3 equações e 5 incógnitas ! Precisamos de mais 2 equações para determinar todas as incógnitas.
Acho que chegou o Momento de perguntar quais são essas 2 equações, certo? Vamos trabalhar com o equilíbrio de momentos na direção na direção do eixo :
E:
Resolvendo o sistema de equações acima:
Resposta
Exercício Resolvido #9
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 113, 3/110
Cada uma das três barras uniformes de tem uma massa de . As barras estão soldadas juntas na configuração mostrada e estão suspensas por três arames verticais. As barras e estão no plano horizontal e a terceira barra está em um plano paralelo ao plano .Calcule as forças trativas em cada arame.
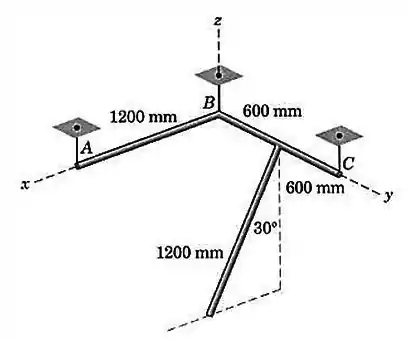
Passo 1
O diagrama de corpo livre da nossa estrutura fica assim:
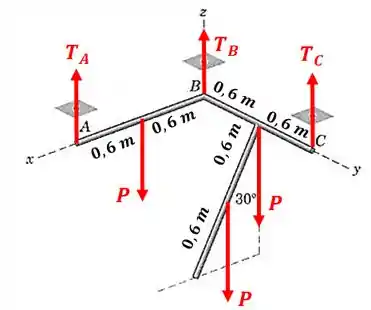
Como todas as barras são uniformes e possuem a mesma massa de , a força peso de todas elas são iguais:
Passo 2
Vamos começar calculando o momento com relação ao eixo , pois duas das nossas incógnitas ( e ) estão sobre este eixo e, portanto, não vão ter braço de alavanca.
Passo 3
Vamos fazer o somatório de momentos com relação ao eixo agora:
Repare que o braço de alavanca da força peso da barra inclinada será:
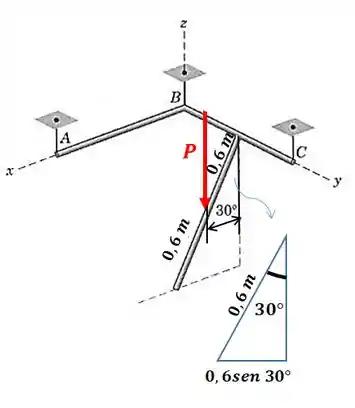
Então:
Passo 4
Vamos usar o equilíbrio de forças para achar a força que falta:
Resposta
Exercício Resolvido #10
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 113, 3/110
Determine a força trativa necessária para manter o sólido retangular na posição mostrada. O sólido retangular com é homogêneo. O atrito em é desprezível.
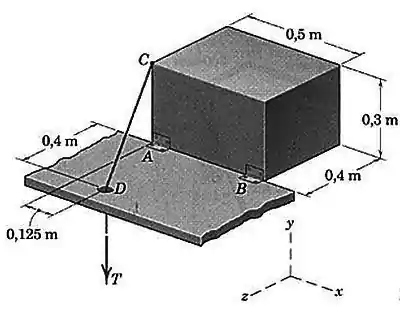
Passo 1
O diagrama de corpo livre do sólido fica assim:
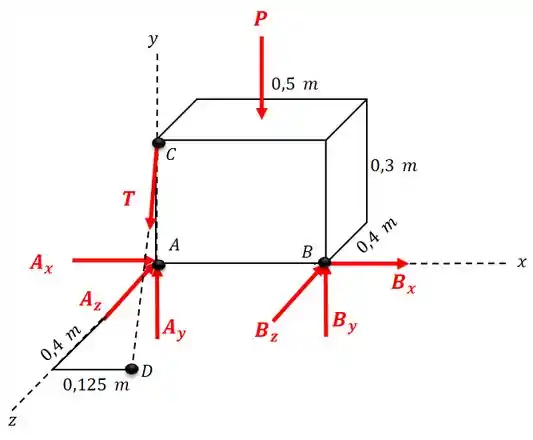
Passo 2
Vamos calcular o módulo da força peso do sólido:
E a foça trativa ? Temos que calcular a sua direção e sentido que é dada pela reta que vai do ponto em direção ao ponto :
Temos que as coordenadas dos pontos e são:
E:
Então:
Então, o vetor normalizado fica:
Então, a força trativa fica:
Passo 3
Vamos começar calculando o momento em relação à reta que esta no eixo , pois as incógnitas de reação de apoio dos pontos e não terão braço de alavanca com relação a este eixo:
Perceba que somente a componente da força trativa terá braço de alavanca com relação à reta , pois a componente é paralela a esta reta e a componente tem sua linha de ação cruzando a reta .
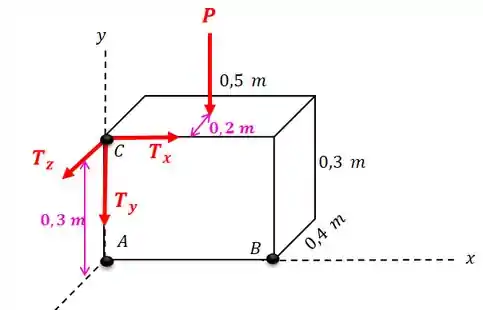
Então:
Resposta
Exercício Resolvido #11
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 113, 3/104
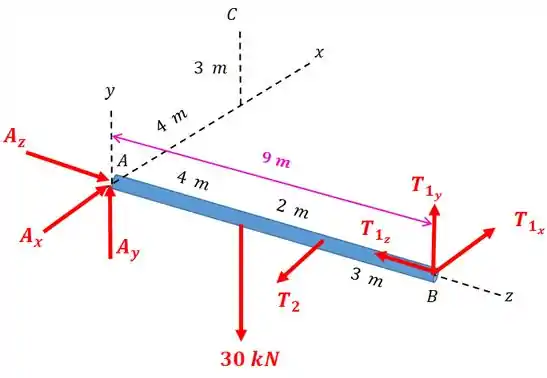
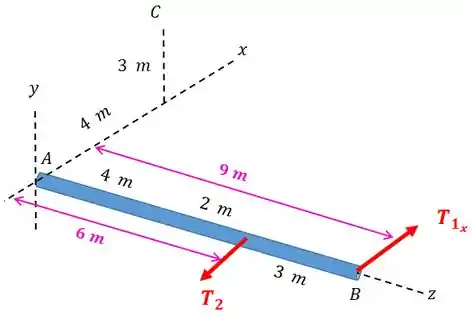
Se o peso do mastro é desprezível comparado à carga de aplicada, determine as forças trativas e nos cabos e a força atuando na rótula em .
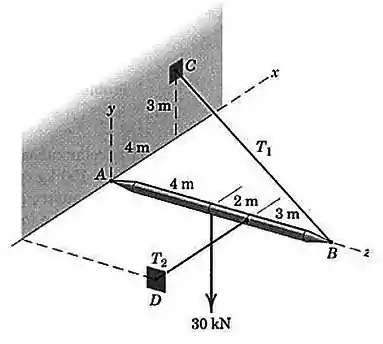
Passo 1
O diagrama de corpo livre fica assim:
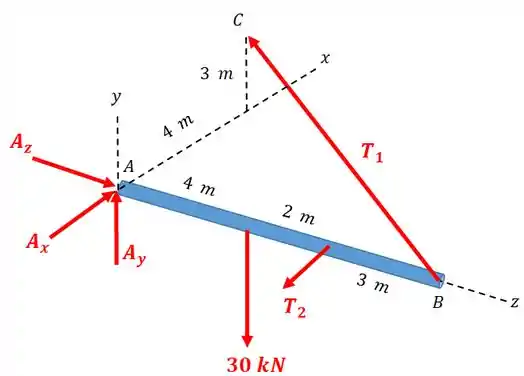
Passo 2
Temos que calcular a direção e sentido da força trativa que é dada pela reta que vai do ponto em direção ao ponto :
Temos que as coordenadas dos pontos e são:
E:
Então:
Então, o vetor normalizado fica:
Então, o vetor da força trativa fica:
Já o vetor é paralelo ao eixo , então podemos escrever:
Passo 3
Vamos começar calculando o momento em relação ao eixo :
Repare que somente a componente da força vai ter braço de alavanca com relação ao eixo :
Então:
Passo 4
Agora vamos calcular o momento com relação ao eixo . As forças que exercem momento com relação a este eixo são:
Então:
Passo 5
Para achar as reações de apoio, vamos fazer o somatório das forças:
Vamos ter que separar as equações de acordo com as componentes:
Então, a reação é:
A reação é:
E a reação fica:
Então, o vetor é:
E a resultante fica:
Resposta
Exercício Resolvido #12
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 113, 3/108
Uma força vertical no pedal do dispositivo é necessária para produzir uma força trativa de na barra de controle vertical. Determine as reações correspondentes nos mancais em e .
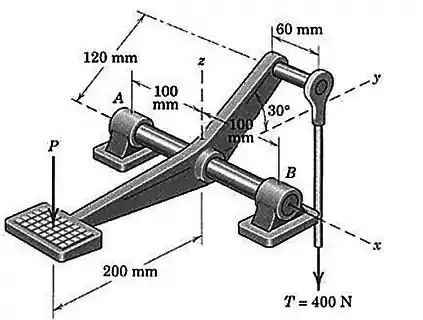
Passo 1
O diagrama de corpo livre fica assim:
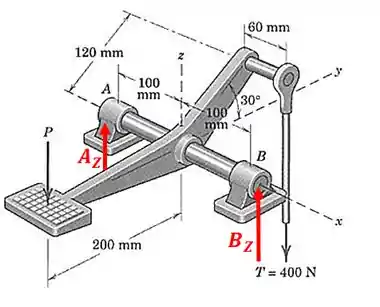
Passo 2
Vamos começar calculando o momento em relação ao eixo :
Repare que a distância da força até o eixo é:
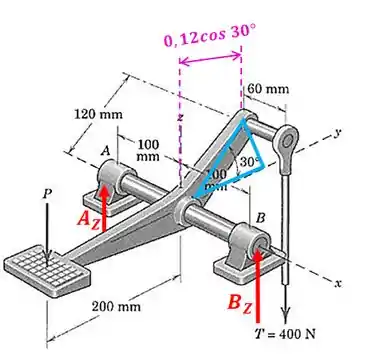
Então:
Passo 3
Agora vamos fazer o somatório de momentos com relação a uma reta que passe pelo ponto e que seja paralela ao eixo :
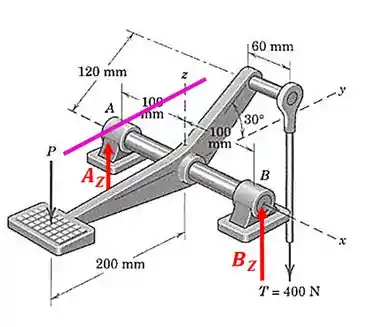
Então:
Passo 4
Para achar as reações de apoio, vamos fazer o somatório das forças:
Como não há nenhuma força no eixo , então não vai ter reações neste eixo nos apoios em e .
Resposta
Exercício Resolvido #13
R.C. Hibbeler, Mecânica para engenharia, Estática, 12° ed. SP: Pearson Prentice Hall, 2011, 171, 5/66
Determine o local e do ponto de aplicação da força de modo que a tração desenvolvida nos cabos , e seja a mesma. Despreze o peso da chapa.
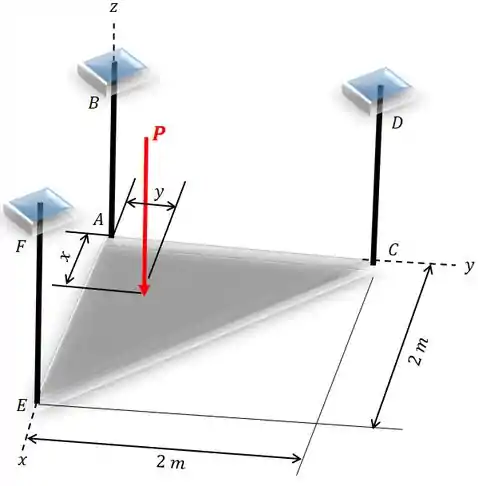
Passo 1
O diagrama de corpo livre fica assim:
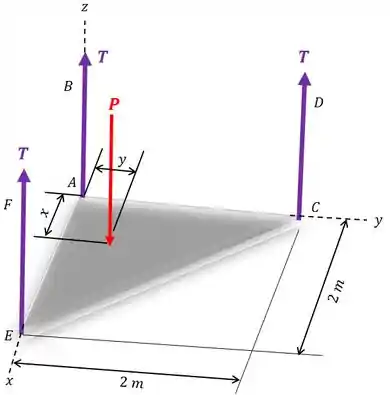
Passo 2
Vamos começar fazendo o equilíbrio de forças verticais:
Vamos deixar esta informação guardada!
Passo 3
Agora vamos calcular o somatório de momentos com relação ao eixo :
Repare que todas as forças que cruzam o eixo não tem braço de alavanca e, portanto, não exercem momento com relação a este eixo!
Sabemos que:
Então, vamos substituir isso na equação do momento:
Cortando , temos:
Passo 4
Agora vamos fazer o somatório de momentos com relação ao eixo :
Já sabemos que:
Então:
Resposta
Exercício Resolvido #14
R.C. Hibbeler, Mecânica para engenharia, Estática, 12° ed. SP: Pearson Prentice Hall, 2011, 171, 5/78
A placa possui um peso com centro de gravidade em . Determine a tração desenvolvida nos fios , e se a força é aplicada em .
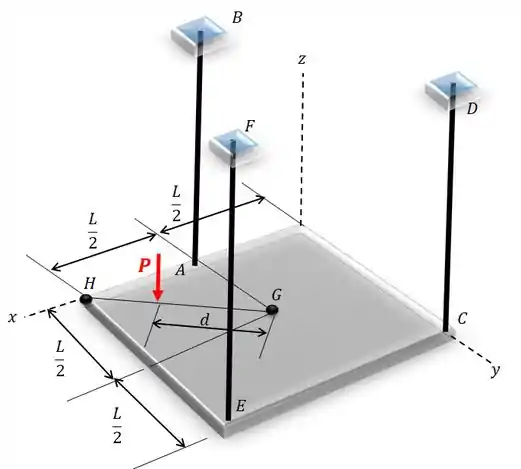
Passo 1
O diagrama de corpo livre fica assim:
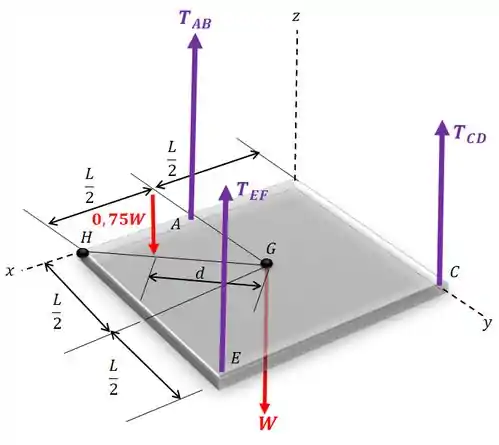
Passo 2
Vamos começar calculando o somatório de momentos com relação a reta que liga os pontos e :
Com isso, ficamos com apenas uma incógnita que é a força trativa .
Mas antes temos que descobrir a distância da força até a reta . Para isso vamos fazer semelhança de triângulos:
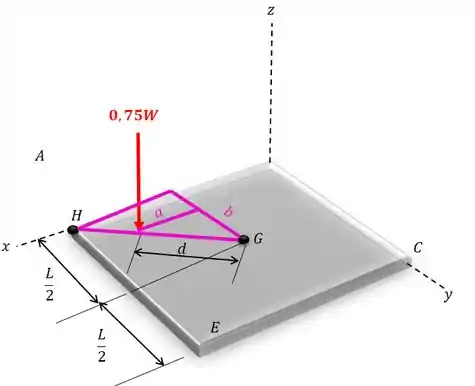
Temos que:
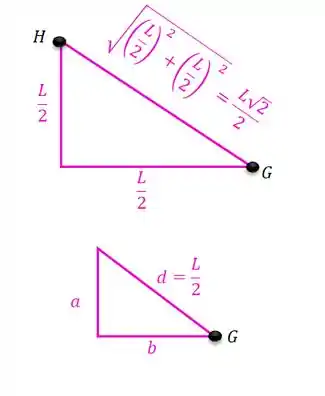
Repare que para achar a hipotenusa do triângulo maior foi feito Teorema de Pitágoras!
Para achar o lado do triângulo menor, temos que:
Sabendo que , temos que:
E o lado será igual ao lado , pois:
Passo 3
Agora sim podemos calcular o momento com relação a reta que liga os ponto e . Sabendo que os braços de alavanca são:
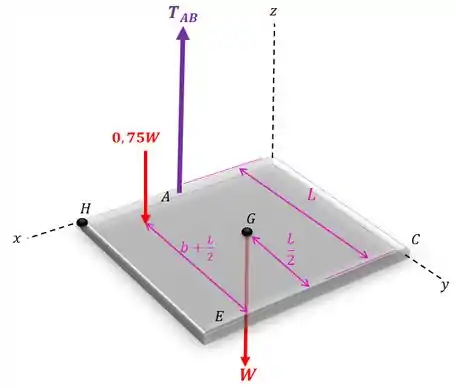
Então:
Podemos cortar o de todos os termos:
Passo 4
Agora vamos fazer o momento com relação ao eixo :
Para isso vamos ter os seguintes braços de alavanca:
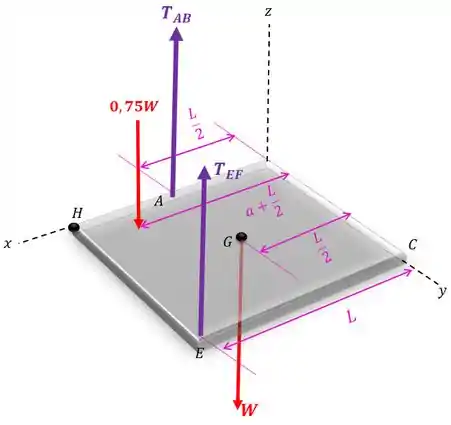
Novamente podemos cortar o de todos os termos:
Passo 5
Para finalizar, vamos fazer o equilíbrio de forças verticais:
Resposta
Exercício Resolvido #15
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 113, 3/81 - Modificada
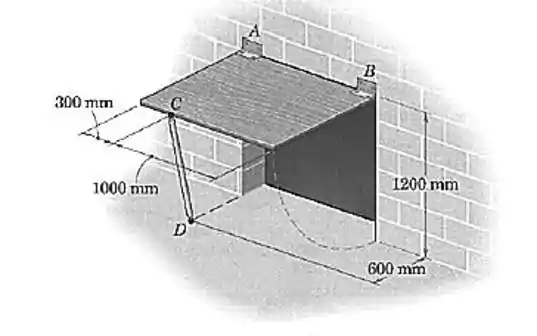
A porta retangular de acesso com é mantida na posição aberta, a , pelo apoio simples . Determine a força no apoio e o módulo da força normal ao eixo de abertura em cada pequena dobradiça e . Considere que na dobradiça a força horizontal e paralela à parede seja nula.
Passo 1
Podemos representar o sistema com o desenho abaixo:
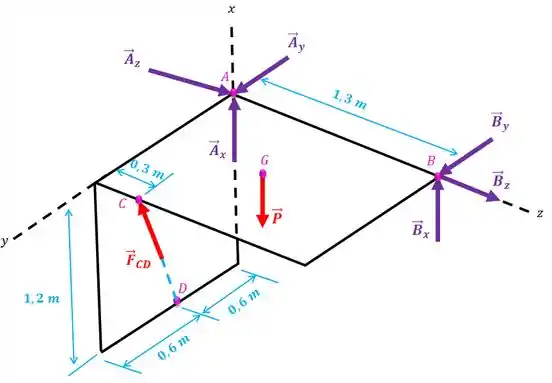
Nós não sabemos quanto vale o módulo da força , mas sabemos calcular a direção dela. Repare que o ponto tem as seguintes coordenadas:
E as coordenadas do ponto são:
Então, a direção é:
Agora temos que transformar isso em um vetor unitário, para isso é só dividirmos pelo seu módulo. Então, vamos começar calculando o módulo:
Então, o vetor unitário vai ser:
Agora sim podemos calcular a nossa força :
Como não sabemos o valor de , vamos deixar assim!
Passo 2
Nosso próximo passo é calcular o módulo da força peso da porta:
Agora que conhecemos todas as forças vamos calcular o momento de cada uma delas com relação aos eixos , e . Vamos escrever a força em termos de suas componentes para facilitar a visualização:
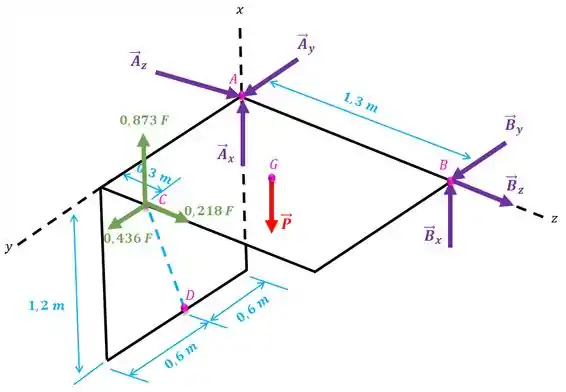
Vamos começar pelo eixo .
Repare que somente o peso e a componente da força exercem momento com relação ao eixo . Isso porque as outras forças não possuem braço de alavanca. Então, vamos lá:
No eixo , a força , o peso e a componente da força possuem braço de alavanca com relação a este eixo:
Como já sabemos o valor do , temos que:
E por último no eixo , as forças que exercem momento são e a componente da força :
Passo 3
Vamos usar o equilíbrio de forças para achar as forças que faltam:
No eixo
No eixo só temos as forças e , então elas vão ser nulas:
O enunciado nos diz para considerarmos a força horizontal e paralela à parede da dobradiça como nula! Essa força que ele tá falando nada mais é do que , assim
Então, a resultante das reações nos pontos e são:
E a força fica: