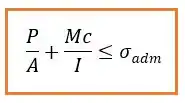Colunas com cargas excêntricas
Teoria
Meus queridos coleguinhas tudo bom com vocês? Hoje quero fazer uma pergunta para as senhoritas e para os senhoritos.
A gente já viu como funciona a flambagem para alguns tipos de colunas mas agora eu pergunto a vocês: como a gente iria fazer para dimensionar uma coluna sujeita a um carregamento excêntrico de modo a resistir à flambagem?
Cargas excêntricas
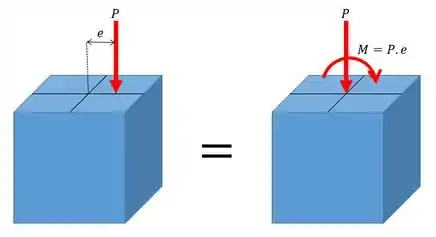
Primeiro vamos lembrar o que é um carregamento excêntrico. Esse tipo de carregamento é aquele que atua numa linha diferente da linha central da nossa coluna, como na figura abaixo.
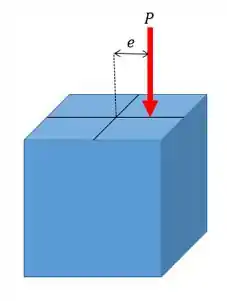
Esse é o paranauê de hoje e para a gente começar a discutir sobre isso a gente deve lembrar que uma carga excêntrica pode ser dividida em uma carga centrada mais um momento puro. Ou seja, vamos ter o seguinte.
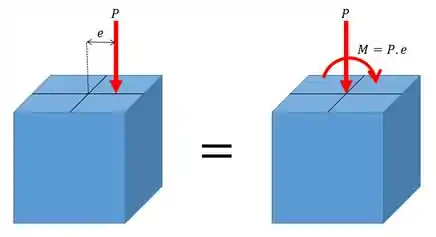
A carga centrada não muda de valor, muda apenas de posição, enquanto um momento puro com valor igual à carga vezes a distância é adicionado de forma a manter o mesmo carregamento.
Tensão resultante de um carregamento excêntrico
Beleza, a gente viu como que podemos dividir um carregamento excêntrico em uma centrada mais um momento. Agora vai mais uma pergunta, como que vai ficar a tensão resultante de um carregamento excêntrico?
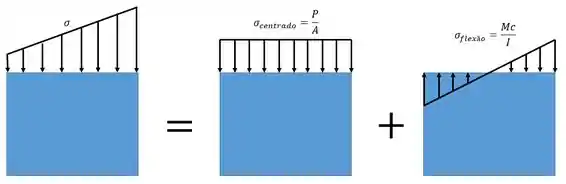
Ora, se a gente já acabou de ver que podemos dividir em um carregamento centrado mais um momento então a tensão resultante vai ser a tensão do carregamento centrado mais a do momento puro (momento puro aqui é a tensão de flexão, é a mesma coisa).
Métodos de resolução
Beleza, pessoal, a gente conseguiu relembrar como que o carregamento excêntrico funciona e como que fica a tensão resultante. Mas a gente ainda não respondeu como aplicar isso à flambagem!
Existem dois métodos que são muito utilizados, são eles: método (ou fórmula) da interação e o método da tensão admissível.
Vamos abordar esses dois métodos agora com o problema prática abaixo, iniciando pelo método da interação.
Pessoal, uma coisa importante!! Sempre que nós estivermos diante de uma coluna com geometria que permite mais de um índice de esbeltez então a gente tem que considerar sempre o maior desses índices. Isso é feito de modo a elevar o fator de segurança das colunas.
Métodos da interação
A gente acabou de ver que a tensão pode ser dada por
Onde
Dessa forma a gente vai ter que a tensão admissível é dada por
Para este método a gente vai dividir ambos os termos pela respectiva tensão admissível, obtendo o seguinte:
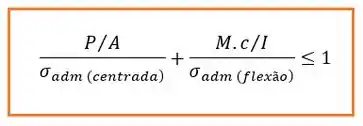
Aqui a tensão admissível pode ser dada diretamente pelo problema ou calculada através de equações conhecidas e que variam com o material e o índice de esbeltez. Algumas dessas equações estão mostradas nas tabelas no “resuminho” no final da nossa aulinha.
Mas por que você me pergunta, jovem gafanhoto? Porque a gente não quer que as tensões sejam maiores do que as admissíveis, correto? Por isso o sinal de .
Uma outra coisa muitíssimo importante para a gente saber é que esse método só pode ser utilizado se:
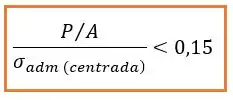
Se essa condição não for satisfeita então não podemos utilizar esse método!
Meus abiguinhos, a gente tá utilizando o exemplo de uma força que está deslocada em apenas um eixo, por esse motivo aparecerá apenas uma tensão de flexão (devido a um momento puro). Caso estejamos tratando de uma carga excêntrica com relação a mais de um eixo a gente deve introduzir os respectivos momentos e consequentemente as respectivas tensões de flexão, obtendo uma forma geral do seguinte formato:
Visualizando como seria isso a gente tem o desenho abaixo.
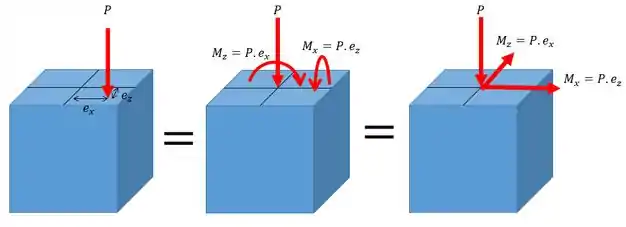
Obs: Nessa figura o segundo e terceiro desenho representam exatamente a mesma coisa, a única diferença entre os dois é que foi aplicada a regra da mão direita.
Outra coisa importante a ser dita é que as distâncias e dependem apenas da posição de aplicação da força em relação ao centro e são utilizadas para o cálculo dos momentos.
Enquanto as distâncias e dependem apenas da geometria da seção transversal e representam a maior distância entre a linha neutra e a superfície do corpo (no caso a coluna). Beleza pessoal?
O método é basicamente esse, galera. A gente tem que dividir a força em carregamento centrado mais momentos e achar a tensão de cada termo. Ao somar todas as tensões e dividi-las pelas respectivas tensões admissíveis não podemos exceder o valor de 1.
Métodos da tensão admissível
Começa bem parecido com o outro, partindo da seguinte equação das tensões:
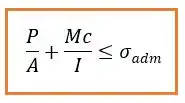
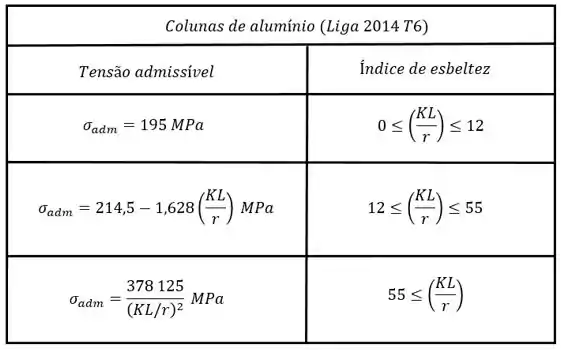
A diferença aqui é que o termo da tensão admissível é dado por diversas equações obtidas experimentalmente para carregamentos concêntricos e dependem do material e do índice de esbeltez ou . É importante notar que sempre vamos escolher o maior índice de esbeltez da coluna.
Para ajudar vocês, meus amores, vou colocar essas equações experimentais no formato de tabelas, é importante observar que a letra que das tabelas representa o raio de giração.
Pessoal, aqui forneci apenas a tabela do aço que é uma tabela mais geral. Abaixo, no resumo, estão as tabelas para o alumínio e a madeira. Lembrando que esses valores são diferentes para diferentes tipos de madeira, aço e alumínio. Sempre preste bastante atenção para utilizar a tabela correta, beleza?
Resuminho
A primeira coisa que temos de lembrar é transformar a carga excêntrica num carregamento centrado mais um momento puro:
Depois aplicar as tensões respectivas:
E vamos obter:
Para o método da interação a gente divide tudo pela tensão admissível e o valor final deve ser menor do que 1:
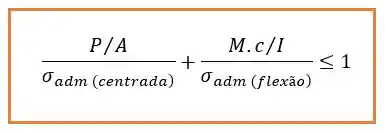
No caso de a carga ser excêntrica em relação a mais de um eixo vamos ter:
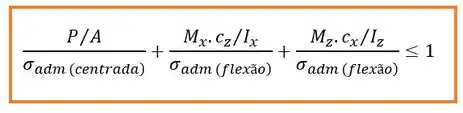
Para o método da tensão admissível a gente faz quase a mesma coisa, a única diferença é que ao invés de dividir tudo pela tensão admissível a gente utiliza dados experimentais para o valor de que são calculados por meio das tabelas.
Métodos de resolução
Métodos da interação
Métodos da tensão admissível
Resuminho
Exercícios Resolvidos
Exercício Resolvido #1
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 512. Problema 13.105 (Adaptado)
A coluna de alumínio com perfil está sob uma carga de aplicada de modo excêntrico conforme a figura. Sabendo que essa coluna está engastada na base e livre no topo, calcule o valor da tensão axial e da tensão de flexão atuantes na viga.
Passo 1
Fala aí, galera!! Esse tópico exige muitas contas então vamos começar com um exercício um pouco mais simples e vamos calacular as duas tensões que agem na nossa viga.
- Tensão axial – Essa tensão é fornecida pela equação da carga centrada (aquela da tabela).
- Tensão de flexão – Essa tensão é calculada pela equação
Por enquanto é isso que precisamos saber!
Passo 2
A gente acabou de ver que vamos ter duas tensões, correto? A axial e a de flexão. Vamos ver como isso funciona um pouco melhor fazendo a transformação de uma força excêntrica em uma força centrada mais um momento:
A gente precisa só saber qual o valor desse momento, não é mesmo? Ele vai ser dado pela força vezes a distância .
Pessoal! A força vertical será a responsável pela tensão axial enquanto o momento pela tensão de flexão!
Passo 3
Para achar a tensão axial é só pegar a carga centrada e dividir pela área:
A força vale e a área é tabelada para o perfil :
Substituindo a gente vai ter:
Passo 4
Mas não existe apenas o componente axial, correto? Temos que calcular o componente axial também! Essa componente é dada por:
O momento a gente já calculou lá no passo 2 e vale:
A tensão vai ocorrer no eixo em torno do eixo então temos que ter o momento de inércia em relação à esse eixo:
Falta só o valor de , para isso a gente precisa olhar o perfil da nossa coluna :
No caso desse tipo de perfil a gente vai ter quase sempre que é metade da altura . Para esse perfil temos que:
Assim,
Agora basta substituir na equação da tensão de flexão:
Resposta
Exercício Resolvido #2
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 512. Problema 13.105 (Adaptado)
A coluna de alumínio com perfil está sob uma carga de aplicada de modo excêntrico conforme a figura. Sabendo que essa coluna está engastada na base e livre no topo, verifique se a coluna resiste à carga aplicada segundo o método da tensão admissível.
Passo 1
Pessoal, esse exercício é quase igual ao anterior. A única diferença é que agora a gente vai saber se essa coluna vai resistir ou não, ao invés de só calcular as tensões que atuam nela.
Então se você já viu o exercício anterior e entendeu pode pular para os passos 2,3 e4. Se você não viu o exercício anterior não tem problema, é só acompanhar todos os passos =D
Vamos lembrar que:
- Tensão axial – Essa tensão é fornecida pela equação da carga centrada (aquela da tabela).
- Tensão de flexão – Essa tensão é calculada pela equação
Passo 2
A gente acabou de ver que vamos ter duas tensões, correto? A axial e a de flexão. Vamos ver como isso funciona um pouco melhor fazendo a transformação de uma força excêntrica em uma força centrada mais um momento:
A gente precisa só saber qual o valor desse momento, não é mesmo? Ele vai ser dado pela força vezes a distância .
Pessoal! A força vertical será a responsável pela tensão axial enquanto o momento pela tensão de flexão!
Passo 3
Para achar a tensão axial é só pegar a carga centrada e dividir pela área:
A força vale e a área é tabelada para o perfil :
Substituindo a gente vai ter:
Passo 4
Mas não existe apenas o componente axial, correto? Temos que calcular o componente axial também! Essa componente é dada por:
O momento a gente já calculou lá no passo 2 e vale:
A tensão vai ocorrer no eixo em torno do eixo então temos que ter o momento de inércia em relação à esse eixo:
Falta só o valor de , para isso a gente precisa olhar o perfil da nossa coluna :
No caso desse tipo de perfil a gente vai ter quase sempre que é metade da altura . Para esse perfil temos que:
Assim,
Agora basta substituir na equação da tensão de flexão:
Passo 5
Beleza, galera a gente já achou as tensões que atuam na coluna:
Agora vamos ver se a coluna aguenta essas tensões!!
Para qualquer dos métodos que podemos utilizar a primeira coisa que temos de fazer é calcular o índice de esbeltez. Tal índice é calculado a partir do comprimento , fator de comprimento efetivo e o raio de giração :
Pessoal, o comprimento já foi dado e vale , como a coluna está engastada na base e livre no topo temos que e o raio de giração é obtido a partir da seguinte equação entre o momento de inércia e a área:
Como estamos tratando com um perfil vamos ter que:
Pessoal, lembrem-se que a gente precisa sempre utilizar o menor raio de giração!! Então temos que utilizar o menor momento de inércia para esse cálculo:
Substituindo na equação para achar o valor do raio de giração:
Agora podemos achar o valor do índice de eslbetez!
Passo 6
Galera, a gente já ta no final da resolução desse exercício. Agora vamos calcular a tensão admissível, para isso vamos utilizar a tabela para o alumínio que é a seguinte:
Observe que o valor do índice de esbeltez é maior do que 55:
Logo vamos ter que utilizar a terceira equação:
Aí é só substituir né pessoal!
Para esse método a gente precisa achar a tensão máxima e comprar acom a tensão admissível . A tensão máxima é dada pela soma da axial com a de flexão:
Observe que está bem acima do limite da tensão admissível
Portanto essa coluna não irá resistir ao esforça da força!!!
Resposta
Observe que está bem acima do limite da tensão admissível
Portanto essa coluna não irá resistir ao esforça da força!!!
Exercício Resolvido #3
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 514. Problema 13.112 (Adaptado)
Uma coluna de aço engastada na base e livre no topo sofre um carregamento deslocado de do eixo central como mostrado na figura. Determine se essa coluna é segura com base no método da interação. Dados: . Tensões admissíveis ; .
Passo 1
Como podemos ver o problema está falando sobre flambagem no caso de uma carga excêntrica e pede para verificarmos se a carga aplicada à coluna está acima ou abaixo do limite permitido, o problema pede para que façamos essa análise com base no método da interação.
Com isso a gente pode verificar alguns pontos:
- A seção transversal é um quadrado e, portanto, tem o mesmo momento de inércia para ambos os eixos. Sendo assim não precisamos nos preocupar com o eixo onde ocorre a flambagem.
- Nós temos de utilizar a tabela experimental para colunas de aço dado abaixo, sendo assim precisamos achar o valor do índice de esbeltez para saber qual equação utilizar.
- Utilizando a equação correta da tensão admissível
Passo 2
Vamos começar calculando o índice de esbeltez da coluna
Como a coluna está engastada na base e livre no topo temos que , a altura da coluna é , agora falta achar o raio de giração , que pode ser achado através da relação entre o momento de inércia e a área.
O momento de inércia do nosso quadrado é
E a área
Sendo assim vamos ter o raio de giração
Logo, podemos calcular o valor do índice de esbeltez:
E o índice de esbeltez comparativo. Esse valor é inerente ao material, não dependendo da geometria da coluna:
Show! Agora temos os dois valores e podemos utilizar a tabela para fazer a comparação e saber qual equação utilizar.
Passo 3
A tabela é a seguinte.
Como a gente já calculou os dois índices de esbeltez, basta comparar os termos e vamos ter:
Logo,
Ou seja, vamos utilizar a primeira equação para o cálculo da tensão admissível.
Logo, vamos obter
Passo 4
Agora podemos aplicar a equação da interação:
Aqui nós não temos nem o momento nem o valor de , então vamos calcular o momento a partir do valor da força excêntrica da forma
Como e
O valor de é igual a maior distância da linha neutra até a superfície da peça. Olhando a seção transversal nós vamos ter
Sendo assim
O resto dos valores nós já temos então vamos substituir na equação
Então por enquanto está tudo certinho!
Passo 5
A gente só precisa fazer uma última verificação. Isso acontece porque algumas normas dizem que esse método da interação só pode ser utilizado quando:
Substituindo
Agora deu ruim! Então veja como isso é importante, utilizando essa norma a coluna até passa no teste. Mas a grande questão é que esse norma não pode ser utilizada nesse caso devido à elevada carga centrada!
Resposta
Apesar da coluna passar no teste do método da integração, este método não pode ser utilizado devido à elevada carga centrada.
Exercício Resolvido #4
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 514. Problema 13.116 (Adaptado)
Determine a carga excêntrica máxima admissível que pode ser aplicada à coluna de madeira engastada na base e livre no topo. Utilize o método da tensão máxima admissível e a seguinte tabela como base.
Passo 1
Faala, galerinha! Agora a gente pode ver que o problema nos traz uma força ecêntrica com relação à dois eixos. Desta forma a gente vai ter duas tensões de flexão, ok?
Então para resolver esse problema a gente vai:
- Dividir a força excêntrica em uma força centrada mais dois momentos.
- Calcular as respectivas tensões (uma axial e duas de flexão).
- Calcular a tensão admissível.
- Comparar o valor da tensão máxima com a tensão admissível.
Passo 2
Vamos fazer um desenho então para ver como a nova força e os momentos vão ficar:
Vamos achar o valor de cada momento fazendo:
Então vamos ter:
Pessoal! A força vertical será a responsável pela tensão axial enquanto os momentos pelas tensões de flexão!
Passo 3
Para achar a tensão axial é só pegar a carga centrada e dividir pela área:
Calculando a área:
Substituindo a gente vai ter:
Como a gente não tem o valor de então vamos deixar assim =D
Passo 4
As componentes de flexão vão ser dadas por:
Calculando a tensão de flexão no eixo a gente vai ter:
A gente já tem o momento em :
Podemos calcular o momento de inércia em :
E o valor de
substituindo vamos achar:
Passo 5
Agora vamos calcular o valor da a flexão em :
A gente já tem o momento em :
Podemos calcular o momento de inércia em :
E o valor de
substituindo vamos achar: