Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 52
5/52) As duas engrenagens formam uma unidade integrada e giram sobre a cremalheira fixa . A engrenagem maior tem dentes , e a rosca sem fim gira com uma velocidade de . Determine a velocidade do centro da engrenagem .
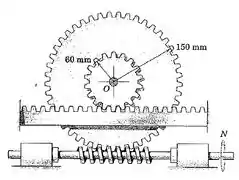
Passo 1
Então galera , nós sabemos que , pelas relações aprendidas nesta seção :
Logo ,
Além disso , como o sistema é acoplado , podemos afirmar que a velocidade angular em cada ponto da engrenagem é a mesma . Dessa forma ,
Então ,
Passo 2
Bom galera distância entre os dentes da engrenagem mais larga é dada pelo comprimento da circunferência dividida pelo número de dentes da engrenagem :
Sendo assim , é o avanço por revolução da engrenagem .
Consequentemente ,
Então ,
Resposta
Exercícios de Livros Relacionados
Em um mecanismo projetado para converter movimento linear em movimente angular, o cilindro hidráulico fornece ao pino A uma velocidade constante para baixo v durante um curto intervalo de movimento. D
A rotação da alavanca O A é controlada pelo movimento do disco em contato cujo centro recebe uma velocidade horizontal v . Determine a expressão para a velocidade angular ω da alavanca O A em termos d
O carretel gira sobre seu cubo subindo o cabo interno A enquanto a placa compensadora B puxa os cabos externos para baixo. Os três cabos estão firmemente enrolados em torno de suas respectivas perifer
A roda de raio r rola sem deslizar, e seu centro O possui uma velocidade constante v 0 para a direita. Determine expressões para os módulos da velocidade v e da aceleração a do ponto A sobre a borda d
5/53) O acionamento do cilindro hidráulico provoca o alongamento de O B na taxa constante de 0,260m / s . Calcule a aceleração normal no ponto A em sua trajetória circular em torno de C para o instant