Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 89
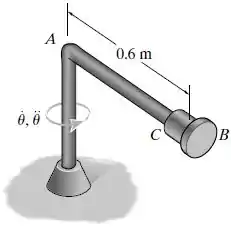
O anel de 0,5 kg pode deslizar livremente ao longo da barra lisa . Em um dado instante a barra está girando com uma velocidade angular de rad/s e tem aceleração angular de rad/s2. Determine a força normal da barra e a reação da placa na extremidade sobre o anel neste instante. Despreze a massa da barra e a dimensão do anel.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do anel :
Velocidade angular da barra :
Aceleração angular da barra :
Comprimento da barra :
Desenhamos o diagrama de corpo livre do anel no instante mencionado:
Onde é a força peso, e é a força normal.
A questão pede para determinarmos a força normal da barra sobre o anel. Está força não é a força . Cuidado!! A força que o enunciado pede é a força normal da barra exercida devido ao seu movimento giratório, ou seja, a força gerada tangencialmente ao seu movimento. No nosso diagrama de corpo livre, esta força está representada por . Logo,
O enunciado também pede a reação da placa na extremidade sobre o anel neste instante. O que ele quer aqui é a força exercida no anel no sentido radial, ou seja, . Logo,
Passo 2
Primeiramente, vamos encontrar as derivadas temporais do anel em ( e ). Sabemos que no instante pedido, , logo
Os valores das derivadas temporais de já são fornecidos pela questão.
Em seguida, vamos encontrar as derivadas temporais em ( e ). Como é constante, seu valor não varia no tempo, resultando em
Passo 3
Sabemos que as componentes da aceleração do anel nas coordenadas , e são dadas por
Logo,
Passo 4
Agora aplicaremos as Equações do Movimento.
Analisando primeiramente no eixo , temos que
Analisando no eixo , temos
Analisando no eixo , temos