Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 96
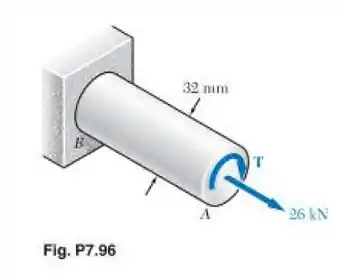
A barra de alumínio fundido indicada na figura é feita de uma liga para a qual e . Usando o critério de Mohr, determine a intensidade do torque T para a qual se espera que ocorra a falha.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, nós vamos utilizar o critério de Mohr para materiais frágeis conforme visto na fig 7.38 nessa seção, onde temos o envoltório seguro, e se o ponto cair fora dele, quer dizer que temos ruptura. Para saber se o ponto está ou não dentro do envoltório, usaremos a seguinte relação:
Essa é a equação da reta no 4º quadrante da fig 7.38, em que é a tensão em um extremo do círculo de Mohr (tensão máxima) e é a tensão no outro extremo (tensão mínima). Então, se o valor encontrado nessa relação for maior que 1, quer dizer que o ponto está fora do envoltório e haverá ruptura, do contrário, a condição é segura.
Para calcular os , precisamos da tensão média e do raio do círculo de Mohr. Só que no nosso caso queremos descobrir a tensão de cisalhamento para a qual se espera que ocorra falha. Então, vamos escrever as tensões e o raio do círculo de Mohr em função da tensão de cisalhamento e depois igualar a equação mostrada à 1, para encontrar a tensão de cisalhamento no caso limite. Depois de obtermos a tensão de cisalhamento, basta aplicar a equação para a tensão de cisalhamento gerada pelo torque aplicado em uma seção circular, dada por:
Isolando o valor do torque chegamos na resposta. Então bora lá!
Passo 2
Vamos começar escrevendo a equação para o raio do círculo de Mohr, que é dada por:
Beleza, nós sabemos que a tensão na direção x é gerada pela força P, ou seja:
Então, vamos calcular a área da seção transversal, que será dada por:
Então, a tensão na direção x será:
E, no nosso caso, não temos nenhuma tensão na direção y, então teremos:
Substituindo os valores conhecidos na equação do raio para o círculo de Mohr, chegamos em:
Agora vamos calcular a tensão média, que é dada por:
Passo 3
Agora, com os valores da tensão média e do raio do círculo, podemos calcular os valores das tensões nos pontos A e B, onde temos:
Agora podemos utilizar a equação que vimos lá no passo 1, onde temos:
Então, substituindo os valores conhecidos na equação acima, teremos:
Passo 4
Beleza! Com essa tensão de cisalhamento, vamos utilizar a equação para a tensão de cisalhamento causada por torção, onde temos:
Em que c é a distância do centro do eixo até o ponto de interesse e J é o momento polar de inércia. No nosso caso, nosso c será o raio do eixo, já que esse é o ponto de máxima tensão de cisalhamento, então teremos:
Agora, nosso momento polar de inércia será dado por:
Então, isolando o torque da equação do cisalhamento teremos:
E, substituindo os valores conhecidos, chegamos em:
Opa! Esse é o torque máximo que pode ser aplicado no nosso eixo! Terminamos mais um exercício, valeeu!