Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 27
Determine a força F entre as mandíbulas da braçadeira em termos de um torque M exercido na alça do parafuso de ajuste. O parafuso tem avanço (avanço por rotação) L e o atrito deve ser desprezado.
Passo 1
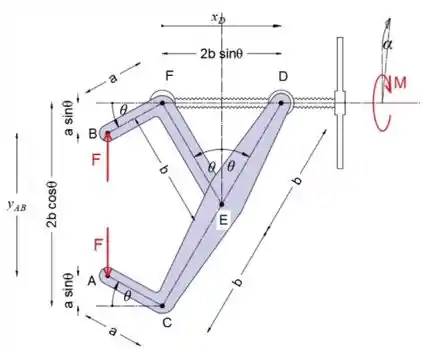
Primeiro, vamos desenhar o diagrama de força ativa, observe que a força de aperto F atua em ambos os pontos A e B, também assumimos que os braços ACE e BFE são retos
Podemos ver no esboço que a mudança de distância AB é
Derive ambos lados da equação
Também podemos ver no esboço que o movimento virtual do ponto D é
Observe que podemos escrever esta distância como função do ângulo a também
Uma vez que o ângulo de 2π é necessário superar a distância L, a distância é igual ao produto do ângulo e razão
Como escrevemos a distância x_D em função de α e θ, podemos determinar a relação entre esses dois ângulos
Derive ambos lados da equação para ter
Passo 2
O trabalho virtual realizado pelo par M é produto da rotação virtual δα e do momento que a força produz
Substituiremos por
(1)
Trabalho virtual feito pela força é
substituiremos por
(2)
Passo 3
A seguir, vamos aplicar o Princípio do Trabalho Virtual, que afirma que a soma do trabalho realizado por todas as forças ativas é igual a zero
Substituiremos e pelas expressões (1) e (2) respectivamente
Dividiremos ambos lados da equação por
Escreveremos F como
multiplicaremos ambos lados da equação por para obter