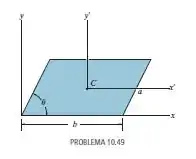
Determine o momento de inércia do paralelogramo em relação ao eixo , que passa pelo centroide da área.
Passo 1
Fala aí! tudo certo?
Nesse problema foi dado um paralelogramo bem esquisito e nosso objetivo é calcular seu momento de inércia em relação ao eixo que passa pelo centroide da área.
Tem ideia de como fazemos isso?
Para resolver esse problema, temos que usar o teorema dos eixos paralelos:
Assim, podemos simplificar a figura a encontrar o resultado.
Saca só!
Passo 2
Vamos começar redesenhando a figura:
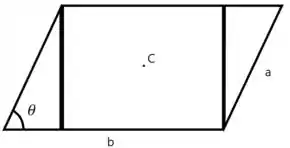
Separando em três formas primitivas, temos que o momento de inércia é:
Se as hipotenusas dos triângulos medem , então a altura do quadrado é:
e também podemos tirar que a largura do quadrado é:
Sendo a base do triângulo.
Começando pelo quadrado, temos que como seu centro também é o centroide da área, temos que:
Tranquilo até aqui?
Passo 3
Agora vamos olhar para os triângulos...
Sabemos a medida da sua altura, sua base e a distância dos seus centroides para o centroide da figura.
Pelo teorema dos eixos paralelos:
Logo:
Simplificando...
Show?
Passo 4
Agora vamos juntar os dois resultados e tentar simplificar o máximo...
É isso! O que achou? Responde Aí!