Determine o produto de inércia da área sombreada em relação aos eixos e .
Passo 1
Oi tudo bem? Vamos resolver este exercício.
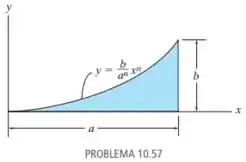
Nesse problema foi dada uma figura hachurada sob a curva de função
Nosso objetivo é encontrar o produto de inércia dessa figura em relação aos eixos e
Lembra como fazemos isso?
Para calcular o produto de inercia de uma figura basta aplicarmos a fórmulinha:
Saca só!
Passo 2
Nesse caso, podemos definir como:
Com variando de a e variando de a .
Assim, nosso produto de inércia é:
Integrando em relação a ...
Aplicando os limites de integração:
Integrando o resultado em relação a ...
Aplicando os limites de integração:
E finalmente, o produto de inércia é:
É isso! Entendeu tudo? Responde Aí!