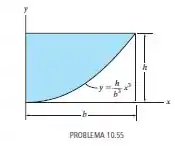
Determine o produto de inércia do área sombreada em relação aos eixos e .
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Deveremos encontrar o produto de inércia a área sombreada em relação aos eixos e .
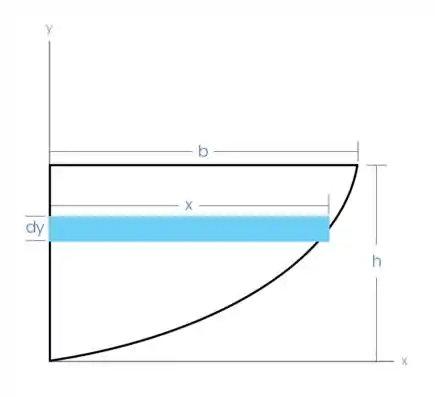
Para esse problema, nós iremos utilizar esse elemento de área como nosso elemento diferencial.
Vamos aos cálculos!
Passo 2
Para determinar o produto de inércia da figura, nós iremos aplicar o teorema do eixo paralelo ao elemento diferencial. Esse teorema nos da a seguinte equação:
Onde:
é o produto de inercia do elemento diferencial sobre os eixos e
é o produto de inercia do elemento diferencial sobre o eixo centroidal
é a área do elemento de área
é a coordenada do centroide do elemento diferencial
é a coordenada do centroide do elemento diferencial
Passo 3
Obtendo a área do elemento diferencial de área:
Note que o centroide do elemento diferencial é localizado em:
E:
Agora nós podemos ter:
Finalmente, nós podemos obter simplesmente integrando