Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 33

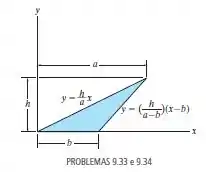
Localize o centroide overset(-)(x) da área sombreada.

Passo 1

Oi tudo bem? Vamos resolver este exercício.

Vamos iniciar desenhando o diagrama de corpo livre mostrando o elemento diferencial da área sombreada.

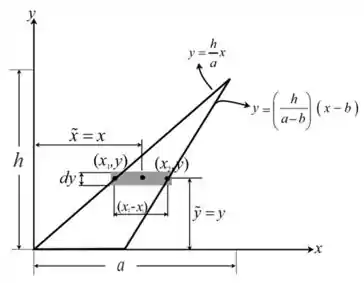
Passo 2

Agora iremos escrever a equação da área sombreada

y = (h)/(a) x_1

x_1 = (a)/(h) y

y = ((h)/(a - b)) (x_2 - b)

x_2 = ((a - b)/(h)) ( y + b )

Vamos calcular a área elementar da área sombreada

d A = (x_2 - x_1) d y

Vamos substituir

d A = ((a - b)/(h)) (y + b) - (a)/(h) y

d A = (b - (b)/(h) y) d y

Passo 3

Vamos calcular o centroide da área do elemento localizado em torno do eixo de x.

bar x = x_1 + (x_2 - x_1)/(2)

bar x = (1)/(2) (x_2 + x_1)

= (1)/(2) (((a - b)/(h)) (y + b) - (a)/(h) y)

bar x = ((a)/(h) y - (b)/(2 h) y + (b)/(2))

Passo 4

Vamos calcular o centroide bar x da área sombreada.

bar x = (int_A bar x d A)/(int_A d A)

bar x = (int_0^h ((a)/(h) y - (b)/(2 h) y + (b)/(2)) [(b - (b)/(h) y) d y])/(int_0^h (b - (b)/(h) y) d y)

= ([(b)/(2 h) (a - b) y^2 + (b)/(6 h^2) (b - 2 a) y^3 + (b^2)/(2) (y)]_0^h)/((b y - (b)/(2 h) y^2)_0^h)

bar x = ([(b)/(2 h) (a - b) (h)^2 + (b)/(6 h^2 (b - 2 a) (h)^3) + (b^2)/(2) (h)] - 0)/((b (h) - (b)/(2 h) (h)^2) - 0)

Passo 5

Vamos simplificar

bar x = ((b h)/(6) (a + b))/((b h)/(2))

bar x = (1)/(3) ( a + b )

Resposta

P o r t a n t o , o c e n t r o i d e bar x d a á r e a s o m b r e a d a é (1)/(3) (a + b) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centro de massa do corpo sólido homogêneo cujo volume é determinado girando a área sombreada em 360 ∘ em torno do eixo z.
Determine as coordenadas do centro de massa do corpo homogêneo.
Determine a altura acima da base do centróide da área da seção transversal da viga. Negligencie os filetes.
Reduza as forças representadas na figura anterior a origem dos sistemas cartesianos indicados. Idem para as forças distribuídas mostradas na figura que se segue
Reduza as forças representadas na figura anterior a origem dos sistemas cartesianos indicados. Idem para as forças distribuídas mostradas na figura que se segue