Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 73

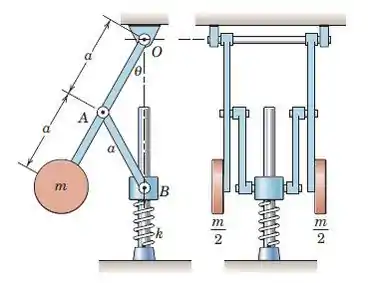
No mecanismo mostrado, a mola de rigidez k é descomprimida quando θ = 60 ∘. Além disso, as massas das peças são pequenas em comparação com a soma das massas dos dois cilindros. O mecanismo é construído de forma que os braços possam balançar além da vertical, como visto na vista do lado direito. Determine os valores θ de equilíbrio e investigue a estabilidade do mecanismo em cada posição. Despreze o atrito.

Passo 1

Primeiro, vamos desenhar o diagrama de força ativa

Observe que não há forças agindo no sistema, então podemos escrever a equação de equilíbrio como

δ V = 0 δ V e + δ V g = 0 (1)

Podemos ver a partir do esboço que a altura he comprimento da mola são os mesmos (uma vez que o centro de massa está sempre na mesma altura do ponto B)

h = l = h 0 - 2 a c o s ⁡ θ

A mola é descomprimida em θ = 60 ∘, então o comprimento descomprimido da mola é

l 0   = h 0 - 2 a c o s ⁡ 60 ∘   = h 0 - a

A mudança no comprimento da mola é então

Δ l = l - l 0 Δ l = h 0 - 2 a c o s ⁡ θ - h 0 - a Δ l = a ( 1 - 2 c o s ⁡ θ )

Passo 2

Escreveremos a expressão da energia potencial gravitacional como

V g = m g h

Substituiremos h por h 0 - 2 a c o s ⁡ θ , em que h 0 é constante

V g = m g h 0 - 2 a c o s ⁡ θ

Derivaremos ambos lados da equação

δ V g = 2 m g a s i n ⁡ θ δ θ (2)

Expressão da energia potencial elástica

V e = 1 2 k ( Δ l ) 2

Substituíremos Δ l por a ( 1 - 2 c o s ⁡ θ )

V e = 1 2 k a 2 ( 1 - 2 c o s ⁡ θ ) 2

Derivaremos ambos lados da equação

δ V e = 1 2 k a 2 ⋅ 2 ( 1 - 2 c o s ⁡ θ ) ⋅ 2 s i n ⁡ θ δ θ δ V e = 2 k a 2 ( 1 - 2 c o s ⁡ θ ) s i n ⁡ θ δ θ (3)

Passo 3

Substituiremos δ V g e δ V e pelas expressões (2) and (3) na equação (1) 2 k a 2 ( 1 - 2 c o s ⁡ θ ) s i n ⁡ θ δ θ + 2 m g a s i n ⁡ θ δ θ = 0 Dividiremos ambos lados da equação 2 a δ θ

k a ( 1 - 2 c o s ⁡ θ ) s i n ⁡ θ + m g s i n ⁡ θ = 0

s i n ⁡ θ [ k a ( 1 - 2 c o s ⁡ θ ) + m g ] = 0 O sistema estará em equilíbrio quando a equação acima for satisfeita:

As soluções possíveis são:

s i n ⁡ θ = 0   ⇒   θ = 0 ∘

E

k a ( 1 - 2 c o s ⁡ θ ) + m g = 0 1 - 2 c o s ⁡ θ = - m g k a 2 c o s ⁡ θ = 1 + m g k a c o s ⁡ θ = 1 2 1 + m g k a   ⇒   θ = a r c c o s ⁡ 1 2 1 + m g k a

Observe que o sistema é estável quando a segunda derivada da equação de equilíbrio é maior que zero

  [ k a ( 1 - 2 c o s ⁡ θ ) s i n ⁡ θ + m g s i n ⁡ θ ] d V d θ > 0

Derive a expressão acima

2 k a s i n 2 ⁡ θ + k a ( 1 - 2 c o s ⁡ θ ) c o s ⁡ θ + m g c o s ⁡ θ > 0 2 k a s i n 2 ⁡ θ - 2 k a c o s 2 ⁡ θ + ( k a + m g ) c o s ⁡ θ > 0 2 k a s i n 2 ⁡ θ - c o s 2 ⁡ θ + ( k a + m g ) c o s ⁡ θ > 0

Substituiremos s i n 2 ⁡ θ by 1 - c o s 2 ⁡ θ

2 k a 1 - 2 c o s 2 ⁡ θ + ( k a + m g ) c o s ⁡ θ > 0 (4)

Para checar a estabilidade do sistema em θ = 0 ,colocaremos os valores de θ em (4)

θ = 0 ∘ 2 k a 1 - 2 c o s 2 ⁡ 0 ∘ + ( k a + m g ) c o s ⁡ 0 ∘ > 0 2 k a ( 1 - 2 ) + k a + m g > 0 - k a + m g > 0 m g > k a

O mecanismo é estável para

k < m g a

Passo 4

Checaremos a estabilidade do sistema em θ = a r c c o s ⁡ 1 2 1 + m g k a Substituiremos c o s ⁡ θ by 1 2 1 + m g k a

2 k a 1 - 2 1 4 1 + m g k a 2 + ( k a + m g ) 1 2 1 + m g k a > 0 2 k a - k a k a + m g k a 2 + 1 2 ( k a + m g ) k a + m g k a > 0 2 k a - ( k a + m g ) 2 k a + 1 2 ( k a + m g ) 2 k a > 0 2 k a - 1 2 ( k a + m g ) 2 k a > 0   / ⋅ ( 2 k a )

Multiplicaremos ambos lados da inequação acima 4 ( k a ) 2 - ( k a + m g ) 2 > 0 Para simplificar esta expressão, vamos substituir k a by x and m g by y

4 x 2 - ( x + y ) 2 > 0 4 x 2 - x 2 - 2 x y - y 2 > 0

3 x 2 - 2 x y - y 2 > 0 Observe que, uma vez que os valores k, a, m e g são positivos, isso significa que x e y também são positivos

Passo 5

Resolveremos a equação quadrática

3 x 2 - 2 x y - y 2 = 0 x = 2 y ± 4 y 2 + 4 ⋅ 3 ⋅ y 2 2 ⋅ 3 x = 2 y ± 16 y 2 6 x = 2 y ± 4 y 6

Raízes da equação quadrática

x = y x = - y 3

Uma vez que ambos x e y são positivos, raiz x = - y 3 é impossível, então a única colução é x = y

Sabendo disso, podemos dizer que para a expressão 3 x 2 - 2 x y - y 2 ser maior que zero, x mastro ser maior que y

x > y

Substitua x por ka e y por m g

k a > m g

Mecanismo é estável para

k > m g a

Resposta

Para  θ = 0  , o sistema é estável se  k < m g a

Para  θ = a r c c o s ⁡ 1 2 1 + m g k a ,  o sistema é estável se  k > m g a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

30- Expresse a força compressiva C no cilindro hidráulico da plataforma para carros em termos do ângulo θ . A massa da plataforma é desprezível comparada com a massa m do veículo.
28- A balança postal consiste de um setor circular de massa m 0 articulado em O e com centro de massa em G . O prato e a haste vertical A B tem massa m 1 e são articulados ao setor circular em B . A e
32- Uma chave de boca antitorque é projetada para ser usada por um tripulante de uma nave espacial onde ele não tem uma plataforma estável contra a qual se empurrar enquanto aperta um parafuso. O pino
31- Determine a força N exercida na tora por cada garra do pegador de lenha mostrado.
33- Uma plataforma automática de carga, projetada para a traseira de um caminhão, está mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em C . As con