Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 72
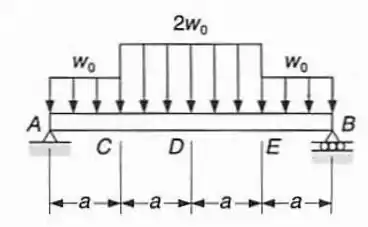
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares,escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o máximo momento fletor da viga.
Passo 1
Agora a gente vai resolver os problemas com a utilização de funções singulares, mas o que é isso? Olha a função abaixo:
Esse é uma função normal, correto? Mas imagina que eu quero fazer o seguinte: Ignorar o segundo termo quando . Nós podemos fazer escrevendo:
Dessa forma vamos admitir duas hipóteses:
Quando a função fica:
Quando a função fica:
Legal né? É essa propriedade que vamos utilizar neste problema.
Passo 2
Vamos calcular as reações nos pontos e . Para isso vamos fazer o somatório das forças em igual a zero (é um problema de estática, lembre-se):
Lembrando que temos cargas distribuídas, assim temos de multiplicar a sua intensidade pela distância.
Como existe uma simetria no problema então a gente pode perceber que , desta forma:
Passo 3
Agora o importante é achar a função singular que define o carregamento, nesse caso será:
Passo 4
Agora a gente vai integrar essa função em de modo a achar o vetor cortante :
Aqui é importante notar que a constante é igual à força de reação. Logo:
Passo 5
Para achar o momento basta que a gente integre novamente =D
Passo 6
Para achar o ponto onde o momento é máximo a gente precisa zera a força cortante. Dessa forma:
Isso ocorre quando .
Desta forma:
Resposta
a)
b)