Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 88
Resolva o Problema 7.87 usando o critério da energia de distorção máxima.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, nós vamos utilizar a equação para a energia máxima de distorção, dada por:
Vamos precisar calcular o valor das tensões em A e B, que são os extremos do círculo de Mohr, fazendo isso, vamos conseguir deixar a equação acima em função da tensão de cisalhamento. Depois de obtermos a tensão de cisalhamento, basta aplicar a equação para a tensão de cisalhamento gerada pelo torque aplicado em uma seção circular, dada por:
Isolando o valor do torque chegamos na resposta. Então bora lá!
Passo 2
Vamos começar escrevendo a equação para o raio do círculo de Mohr, que é dada por:
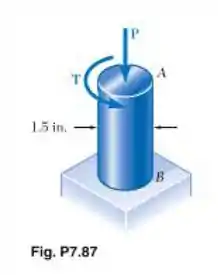
Beleza, nós sabemos que a tensão na direção x é gerada pela força P, ou seja:
Então, vamos calcular a área da seção transversal, que será dada por:
Então, a tensão na direção x será:
E, no nosso caso, não temos nenhuma tensão na direção y, então teremos:
Agora, sabemos que as tensões nos extremos do círculo, pontos A e B serão dadas por:
Então vamos precisar também da tensão média, que é dada por:
Passo 3
Agora, conforme vimos lá no passo 1, temos que a equação para o critério da energia de distorção é dada por:
No nosso caso, estamos interessados no maior valor de torque possível, então temos que considerar o caso limite onde o eixo está para falhar, ou seja, em:
Então, substituindo os valores conhecidos na equação acima, teremos:
Beleza! Agora vamos abrir tudo isso aí:
Isolando a tensão de cisalhamento nessa equação e substituindo os valores da tensão de escoamento e da tensão na direção x teremos:
Passo 4
Beleza! Com essa tensão de cisalhamento, vamos utilizar a equação para a tensão de cisalhamento causada por torção, onde temos:
Em que c é a distância do centro do eixo até o ponto de interesse e J é o momento polar de inércia. No nosso caso, nosso c será o raio do eixo, já que esse é o ponto de máxima tensão de cisalhamento, então teremos:
Agora, nosso momento polar de inércia será dado por:
Então, isolando o torque da equação do cisalhamento teremos:
E, substituindo os valores conhecidos, chegamos em:
Opa! Esse é o torque máximo que pode ser aplicado no nosso eixo! Terminamos mais um exercício, valeeu!