Tensões em Planos Oblíquos
Teoria
Introdução
Sempre que vemos uma barra sob carregamento axial (tração ou compressão pura), o que nós fazemos é avaliar os esforços internos e as tensões nas seções transversais dessa barra.
Mas, de vez em quando, um exercício pode te pedir para calcular as tensões nessa barra em uma outra seção, que não seja transversal:
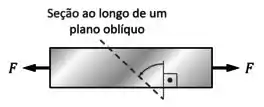
Como que ficam os esforços internos e as tensões nesse caso?
Esforços Internos no Plano Oblíquo
Vamos começar avaliando os esforços internos.
Como sempre, a força normal é normal (perpendicular) à seção e a força cortante é paralela à seção.
Para o equilíbrio da peça, a resultante dessas duas forças e tem que ser igual à força :
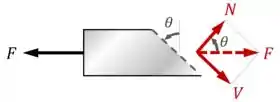
Ao fazer esse desenho acima, você deve tomar muito cuidado para encontrar o valor certo do ângulo com base no ângulo do desenho original do exercício.
Aqui vai uma dica de um bom jeito de pensar em relação a esses ângulos:
Cálculo dos Esforços Internos
A partir desse ângulo entre as forças...
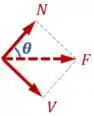
...podemos calcular os esforços internos e em função da força resultante :
Mas atenção! Se o seu ângulo estiver em outra posição, essas relações trigonométricas vão ser diferentes:
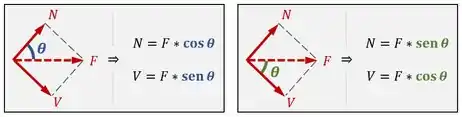
Cálculo da Área da Seção Oblíqua
Calculados os esforços internos e , podemos calcular a tensão normal média e a tensão cisalhante média nessa seção.
Mas para usar essas fórmulas, precisamos antes calcular a área da seção que estamos estudando, que não é a área da seção transversal.
Para encontrar , calculamos primeiro a área usando os dados fornecidos pelo exercício.
Em seguida, tratamos as áreas como se fossem os lados de um triângulo para podermos fazer relações trigonométricas entre elas:
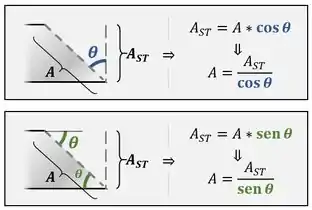
E assim encontramos a área da seção que estamos estudando em função de .
Como você pode ver, mais uma vez a relação trigonométrica é diferente dependendo da posição de no seu desenho.
Cálculo das Tensões
Depois de já ter:
- Desenhado os esforços internos e na seção oblíqua;
- Usado relações trigonométricas para encontrar e em função da força externa ;
- Calculado a área da seção transversal da barra;
- E usado uma relação trigonométrica para encontrar a área da seção oblíqua em relação à área da seção transversal.
Só vai faltar aplicar as fórmulas das tensões normal e cisalhante médias:
E assim você vai ter resolvido seu exercício.
Observação
Alguns exercícios podem pedir que você calcule o ângulo para que ou tenham seus valores máximos.
Para resolver esses exercícios, é bom se lembrar um pouco de cálculo.
Mais especificamente, se lembrar de que os máximos e os mínimos de uma função ocorrem nos pontos em que a sua derivada é igual a zero.
Ou seja, para , por exemplo, temos que:
Esforços Internos no Plano Oblíquo
Cálculo dos Esforços Internos
Cálculo da Área da Seção Oblíqua
Cálculo das Tensões
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 27-1.46.
Os dois elementos de aço estão interligados por uma solda de topo angulada de . Determine a tensão de cisalhamento média e a tensão normal média suportada no plano da solda.
Passo 1
A peça está sendo tracionada por uma força e possui uma seção transversal com área de dimensões .
O exercício quer que a gente avalie a tensão normal média e a tensão cisalhante média em uma seção angulada em relação à horizontal.
Para calcular essas tensões, vamos ter que:
- Fazer uma análise de esforços internos nessa seção inclinada para encontrar a força normal e a força cortante ;
- Observar a geometria da peça para encontrar a área da seção inclinada em função da área da seção transversal.
Passo 2
Vamos começar pela análise de esforços internos na seção inclinada.
Para o equilíbrio das peças, a resultante das forças internas e no plano da solda deve ser igual à força :
Observando essa imagem, tiramos que:
Passo 3
Agora, vamos encontrar a área da seção inclinada em função da área da seção transversal.
Observando a geometria da peça, vemos que :
Passo 4
Agora que , e foram encontrados, podemos aplicar as fórmulas das tensões normal média e cisalhante média:
Substituindo os valores encontrados nos passos anteriores, temos:
Reorganizando essas expressões:
Se quiséssemos só o resultado literal, pararíamos aqui.
Como precisamos dos valores numéricos de e , vamos substituir os valores de , e :
- ;
- ;
Sendo assim, temos:
é a mesma coisa que , então os resultados desses cálculos vão sair em .
Sabendo que e , podemos calcular essas equações, chegando às respostas:
Resposta
Exercício Resolvido #2
Prof. João Chafi Hallack et al., Apostila de Resistência dos Materiais 1, Universidade Federal de Juiz de Fora, Março de 2015, pp. 21-2.
Duas peças de madeira de seção retangular são coladas uma à outra em um entalhe inclinado, conforme mostra a figura. Calcular as tensões na cola para e para:
) ;
) ;
) .
Passo 1
As peças estão sendo tracionadas por uma força e possuem uma seção transversal com área de dimensões .
O exercício quer que a gente avalie a tensão normal média e a tensão cisalhante média em uma seção angulada em relação à horizontal.
Para calcular essas tensões, vamos ter que:
- Fazer uma análise de esforços internos nessa seção inclinada para encontrar a força normal e a força cortante ;
- Observar a geometria da peça para encontrar a área da seção inclinada em função da área da seção transversal.
Feito isso, vamos ter que calcular os resultados para os diferentes valores de : , e .
Passo 2
Vamos começar pela análise de esforços internos na seção inclinada.
Para o equilíbrio das peças, a resultante das forças internas e no plano da cola deve ser igual à força :
Observando essa imagem, tiramos que:
Passo 3
Agora, vamos encontrar a área da seção inclinada em função da área da seção transversal.
Observando a geometria da peça, vemos que :
Passo 4
Agora que , e foram encontrados, podemos aplicar as fórmulas das tensões normal média e cisalhante média:
Substituindo os valores encontrados nos passos anteriores, temos:
Reorganizando essas expressões:
Se quiséssemos só o resultado literal, pararíamos aqui.
Para calcular os valores numéricos, vamos substituir e :
Fazendo a divisão e sabendo que , temos:
Como é um número pequeno, preferimos apresentar os resultados em .
Fazendo isso, obtemos que:
Agora, nos próximos três passos, vamos calcular os resultados para os três diferentes valores de .
Passo 5
Para o item ) , temos:
Sabendo que e , podemos calcular essas equações, obtendo os resultados:
Passo 6
Para o item ) , temos:
Aqui, uma coisa curiosa acontece.
Como , as duas tensões vão obter o mesmo resultado:
Se formos prestar atenção, esse resultado equivale a dividido por .
Passo 7
Finalmente, para o item ) , temos:
Sabendo que e , podemos calcular essas equações, obtendo os resultados:
E assim temos todos os resultados para responder a questão:
Resposta
) , ;
) ;
) , .
Exercício Resolvido #3
Prof. João Chafi Hallack et al., Apostila de Resistência dos Materiais 1, Universidade Federal de Juiz de Fora, Março de 2015, pp. 23-8.
Duas peças de madeira de seção são coladas na seção inclinada como mostra a figura.
Calcular o valor máximo admissível da carga , axial de compressão, dadas as tensões admissíveis na cola de à compressão e ao cisalhamento.
Dica do Expert: e .
Passo 1
Nós precisamos descobrir qual é a máxima carga de compressão nas peças tal que as tensões na cola não ultrapassem os seus valores admissíveis:
- para a tensão normal ;
- E para a tensão cisalhante .
E como podemos fazer isso?
Vamos pensar...
Cada carga vai gerar uma certa força normal e uma certa força cortante na seção inclinada da cola:
Além disso, a seção inclinada da cola possui uma área que é diferente da área de da seção transversal das peças de madeira:
Se encontrarmos as forças e , em função da carga , e a área da seção da cola, podemos usar as fórmulas das tensões normal média e cisalhante média :
Para encontrar as tensões na seção da cola em função da carga .
A partir daí, podemos descobrir qual é a carga que gera uma tensão normal e qual é a carga que gera uma tensão cisalhante .
O menor entre esses dois valores de vai ser a nossa resposta, já que qualquer valor maior geraria pelo menos uma tensão acima da admissível.
Passo 2
Então primeiro, vamos observar os esforços internos na seção da cola para encontrar as forças normal e cortante em função da carga :
Para o equilíbrio dessa peça, a resultante das forças internas e tem que ter a mesma intensidade da força externa e sentido oposto:
Como é o ângulo entre a horizontal (onde a carga atua) e a seção inclinada (onde a cortante atua), podemos desenhar esse ângulo no diagrama de forças e usar seno e cosseno para obtermos que:
Passo 3
Em seguida, vamos encontrar a área da seção da cola.
Se observamos a geometria das peças, conseguimos relacionar a área dessa seção inclinada com a área da seção transversal das peças:
Como seno é o cateto oposto sobre a hipotenusa:
Isolando a área , temos que:
Passo 4
Agora que , e foram encontrados para a seção da cola, podemos usar as fórmulas das tensões normal média e cisalhante média para essa seção:
Substituindo os valores encontrados nos últimos dois passos:
Passando o que está dividindo a área para cima, essas tensões ficam assim:
Passo 5
Para descobrir qual é o valor de que gera uma tensão normal de na seção da cola, partimos da expressão que encontramos no passo anterior:
Isolamos :
E substituímos os valores de , , e :
Lembra aí! , então o resultado desses cálculos vai sair em newtons!
Calculando tudo, obtemos que:
Esse número é um pouco grande, então podemos reescrevê-lo em :
Ou seja, a tensão normal admissível permite cargas de até .
Passo 6
Para descobrir o valor de que gera uma tensão cisalhante na seção da cola, partimos da outra expressão que encontramos no passo 4:
Isolamos :
E substituímos os valores de , , e :
Calculando isso e sabendo que , obtemos:
Reescrevendo em :
Ou seja, a tensão cisalhante admissível requer que a carga não ultrapasse o valor de . Em comparação a tensão normal admissível permite cargas de até !
Então a tensão cisalhante admissível é o fator limitante e o valor máximo admissível da carga é:
Resposta
Exercício Resolvido #4
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 54-1.35.
Um tubo de aço com de diâmetro externo é fabricado a partir de uma chapa de aço com espessura de soldada ao longo de uma hélice que forma um ângulo de com um plano perpendicular ao eixo do tubo. Sabendo que as tensões normal e de cisalhamento máximas admissíveis nas direções, respectivamente, normal e tangencial à solda são e , determine a intensidade da maior força axial que pode ser aplicada ao tubo.
Passo 1
A solda nesse tubo foi feita no formato de uma “rampa em espiral”, formando um ângulo em relação ao plano horizontal.
Além disso, essa solda tem um diâmetro externo , uma espessura , e, consequentemente, um diâmetro interno .
E o que é que o exercício quer?
O exercício quer saber qual é a maior força que pode ser feita no tubo tal que as tensões na solda não ultrapassem os seus valores admissíveis de:
- para a tensão normal ;
- E para a tensão cisalhante .
Precisamos então estudar como afeta as tensões normal e cisalhante na região da solda para descobrir, a partir dos valores admissíveis das tensões, o valor máximo permitido de .
Agora... Para estudar as tensões na região da solda, não podemos estudar a solda inteira, já que a gente não sabe o tamanho total dela.
Então ao invés de estudar a solda inteira, vamos estudar só uma revolução da solda:
Vamos calcular a área da superfície de uma revolução da solda.
Calcular os esforços internos resultantes normal e cortante em uma revolução da solda.
E calcular as tensões normal média e cisalhante média em uma revolução da solda.
Passo 2
Vamos começar então calculando a área da superfície de uma revolução da solda.
A área da seção transversal do tubo pode ser calculada como a diferença entre as áreas de um círculo de diâmetro e outro menor de diâmetro :
Como a área de um círculo em função de seu diâmetro é dada por , então a área fica assim:
Deixando em evidência, temos:
Agora temos que, de alguma forma, relacionar essa área com a área da superfície de uma revolução da solda.
Para fazer isso, vamos “desenrolar” uma revolução do tubo:
Ao fazer isso, a área passa a ser a área da seção horizontal, enquanto a área é a área da seção inclinada :
Daí tiramos que:
Isolando a área , temos:
Substituindo a expressão encontrada para :
Passo 3
O próximo passo é encontrar as forças internas resultantes normal e cortante em uma revolução da solda.
Para fazer isso, vamos mais uma vez usar o tubo “desenrolado”, dessa vez vendo os esforços internos na região da solda:
Para o equilíbrio desse pedaço do tubo, precisamos que a resultante das forças e tenha a mesma intensidade da força , mas sentido oposto:
Dessa imagem, conseguimos tirar que:
E que:
Passo 4
Agora que encontramos , e para uma revolução da solda, podemos encontrar as tensões nessa região e, em seguida, calcular a força correspondente à cada tensão admissível.
Primeiro, vamos fazer esse processo com a tensão normal .
Aplicando a fórmula da tensão normal média:
Substituindo as expressões encontradas nos dois passos anteriores:
Passando o para cima:
Como queremos encontrar o valor de correspondente a um certo valor de , vamos isolar :
Agora podemos substituir os valores:
- ;
- ;
- ;
- E .
- ;
- ;
- ;
- E .
Fazendo isso, temos:
Como , o resultado dessa conta vai sair em newtons ().
Calculando tudo, isso dá:
Como esse número está um pouco grande, reescrevemos ele em :
Isso significa que uma carga de gera na solda a tensão normal admissível de . Qualquer carga maior do que não é permitida nesse tubo.
Passo 5
Agora podemos fazer o mesmo procedimento do passo anterior mas para a tensão cisalhante .
Aplicando a fórmula da tensão cisalhante média:
Substituindo as expressões encontradas para a força cortante e para a área da seção:
Passando o para cima:
Como queremos encontrar o valor de correspondente a um certo valor de , vamos isolar :
Agora podemos substituir os valores:
Fazendo isso, temos:
Calculando tudo e sabendo que , isso dá:
Reescrevendo em :
Ou seja, a tensão cisalhante admissível requer que a força não ultrapasse o valor de .
Em comparação, não são permitidas forças maiores que de acordo com a tensão normal admissível .
Sendo assim, a maior força que pode ser feita no tubo é:
Resposta
Exercício Resolvido #5
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 28-1.51.
Um corpo de prova sob tração com área de seção transversal é submetido a uma força axial . Determine a tensão de cisalhamento média máxima no corpo de prova e indique a orientação de uma seção na qual ela ocorre.
Passo 1
O que está acontecendo?
Dependendo da orientação de uma seção qualquer desse corpo de prova, essa seção vai ter:
- Uma certa força interna cortante , calculada a partir da força externa e do ângulo através de uma análise de esforços internos na seção;
- E uma certa área , calculada a partir do ângulo e da área da seção transversal do corpo de prova.
Então dependendo da orientação de uma seção qualquer do corpo, essa seção vai ter uma certa tensão cisalhante média .
E o que é que o exercício quer?
Ele quer que a gente descubra:
- A tensão cisalhante média máxima nessa peça;
- E a orientação de uma seção onde essa tensão máxima ocorre.
Para fazer isso, temos que calcular , e em função do ângulo .
Daí, vamos poder ver em função de como uma função:
para, em seguida, analisar os máximos dessa função.
Passo 2
Vamos começar calculando a força cortante em função do ângulo .
Fazendo uma análise de esforços internos em uma seção qualquer, vamos encontrar uma força normal e uma força cortante .
Para o equilíbrio das peças, a resultante dessas forças internas e deve ser igual à força externa :
Desenhando corretamente o ângulo nessa figura acima e usando seno & cosseno, encontramos que:
Passo 3
Precisamos calcular também a área de uma seção qualquer em função da sua orientação .
Podemos usar o ângulo para relacionar a área da seção qualquer com a área da seção transversal:
Assim, obtemos que:
Passo 4
Agora que e foram calculados para uma seção qualquer em função da sua orientação , podemos calcular a tensão cisalhante média em função de :
Aplicando a fórmula da tensão cisalhante média para a seção qualquer:
Substituindo as expressões encontradas para e nos passos anteriores:
Reorganizando essa expressão, temos:
Passo 5
Agora que temos a função , precisamos analisar os seus máximos para encontrar .
Para fazer isso, vamos nos lembrar um pouco de cálculo...
Uma função tem seus pontos críticos (pontos de máximo ou de mínimo) quando a sua primeira derivada é igual a zero.
Aplicando isso para a nossa função, temos:
Substituindo a expressão que tínhamos encontrado para :
Como e são constantes, podemos tirar esses termos da derivada:
Dividindo os dois lados por , esses termos somem:
Sabendo que:
- (Regra do Produto);
- ;
- E ,
Essa derivada fica assim:
O que significa que:
O primeiro ângulo com seno e cosseno iguais que conhecemos é o ângulo de .
O que significa que é a orientação de uma seção em que a tensão cisalhante é máxima!
Passo 6
Agora, voltamos para a expressão encontrada para e substituímos para encontrar :
Substituindo :
Como :
O que dá:
Resposta
Exercício Resolvido #6
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 53-1.34.
Uma carga de é aplicada ao bloco de granito mostrado na figura. Determine o valor máximo resultante da () tensão normal e () tensão de cisalhamento. Especifique a orientação do plano no qual ocorre cada um desses valores máximos.
Passo 1
Para descobrir os valores máximos resultantes () da tensão normal média e () da tensão cisalhante média nesse bloco de granito, vamos ter que:
1. Calcular essas tensões para uma seção qualquer do bloco.
Podemos fazer isso:
- Definindo uma seção com uma orientação qualquer ;
- Usando as fórmulas e para calcular as tensões nessa seção qualquer;
- E tomando cuidado para calcular as forças internas normal e cortante e a área da seção de acordo com a orientação dessa seção qualquer.
Além disso, para calcular as forças internas e , vamos usar a informação de que a carga aplicada no bloco é de .
E para calcular a área da seção qualquer, vamos precisar da área da seção transversal do bloco.
2. Estudar os valores máximos das expressões que encontrarmos no passo anterior.
Passo 2
Vamos começar encontrando as forças internas e para uma seção qualquer de orientação :
Para o equilíbrio interno do bloco de granito, a resultante dessas duas forças deve ter sempre uma intensidade igual à carga e um sentido contrário:
Dessa imagem, tiramos que:
Passo 3
Em seguida, podemos encontrar a área de uma seção qualquer em função da área da seção transversal:
Dessa imagem, tiramos que , o que significa que:
Passo 4
, e calculados para uma seção qualquer, agora podemos calculas as tensões em uma seção qualquer.
Começando pela tensão normal média :
Substituindo os valores encontrados para e :
Passando o que está dividindo para cima:
E agora para a tensão cisalhante média :
Substituindo os valores encontrados para e :
Mais uma vez, passando o que está dividindo para cima:
Passo 5
Tanto quanto tem “” em comum, então já podemos deixar esse termo calculado.
Sabendo que e :
Para ter resultados em , podemos reescrever a força de em newtons ():
Calculando, isso dá:
Sendo assim, podemos escrever as tensões e assim:
Passo 6
Enfim, podemos estudar os valores máximos das expressões que encontramos para as tensões e no passo anterior.
Começando pela tensão normal média :
Ela vai ser máxima quando for máximo.
O valor máximo que pode ter é , e isso acontece quando , então temos que a tensão normal média máxima nesse bloco é:
E agora para a tensão cisalhante média :
Ela vai ser máxima quando for máximo.
Para saber quando é máximo, temos que usar um pouco de cálculo.
Em cálculo, vimos que os valores máximos e mínimos de uma função ocorrem quando sua derivada é igual a zero.
Aplicando isso para , temos:
Usando a regra do produto para derivadas e sabendo que derivada de seno é cosseno e derivada de cosseno é menos seno, essa derivada fica assim:
O que significa que:
O primeiro ângulo com seno e cosseno iguais que conhecemos é o ângulo de .
Isso significa que é a orientação de uma seção em que a tensão cisalhante é máxima!
Sendo assim:
Como , temos que , o que significa que:
O que dá:
E assim chegamos às respostas do exercício:
Resposta
() . Ocorre no plano normal do bloco. ( em relação à vertical)
() . Ocorre em um plano com uma angulação em relação à vertical.
Exercício Resolvido #7
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 31,32-1.76.
A estrutura de dois elementos está sujeita à carga distribuída mostrada. Determine a maior intensidade da carga uniforme que pode ser aplicada à estrutura sem que a tensão normal média ou a tensão de cisalhamento média na seção ultrapasse e , respectivamente. O elemento tem seção transversal quadrada de de lado.
Passo 1
A haste faz uma força na viga que contribui para o equilíbrio da viga, como mostra o diagrama de corpo livre da viga:
Como reação, a viga traciona a haste com uma força de mesma intensidade:
Isso significa que podemos usar as equações de equilíbrio na viga para descobrir o valor da tração na haste.
Sabendo o valor da tração na haste, podemos calcular os esforços internos normal e cortante na seção da haste:
Além disso, sabendo que a haste possui uma seção transversal de área , podemos calcular também a área da seção a partir da inclinação da haste:
Sabendo os valores de , e para a seção , podemos calcular também as tensões normal média e cisalhante média nessa seção através de suas fórmulas:
Essas tensões e vão estar, no final das contas, em função da intensidade desconhecida da carga distribuída.
Comparando essas tensões com as tensões máximas permitidas e , vamos poder descobrir os valores correspondentes de .
O menor entre os dois valores encontrados vai ser o valor máximo permitido para , que é o que o exercício quer!
Passo 2
Vamos começar então encontrando a força de tração na haste.
Para tanto, podemos fazer um diagrama de corpo livre (“DCL”) da viga para poder relacionar a força com a intensidade da carga distribuída:
Para deixar nossa vida mais fácil, substituímos a carga uniforme de intensidade , que age em uma região de , por uma força equivalente que age no centro dessa região:
Agora, podemos aplicar uma condição de equilíbrio para tentar relacionar e .
A condição de equilíbrio que vai nos permitir relacionar esses valores mais facilmente vai ser o equilíbrio de momentos em relação ao ponto :
Agora vamos pensar...
A força vai gerar em relação ao ponto um momento no sentido horário () com um braço de .
Quanto a força , não está muito claro qual é o braço dessa força.
Para ficar mais fácil de calcular o momento gerado por , podemos decompor essa força usando a inclinação da haste:
Dessa forma, podemos calcular os momentos gerados pelas componentes de :
- A componente vertical não vai gerar nenhum momento em relação ao ponto (ela vai ter um braço ).
- E a componente vai gerar um momento no sentido anti-horário () com um braço de .
Além disso, da decomposição de , temos que:
Voltando para o nosso equilíbrio de momentos:
Tendo em mente o que acabamos de ver, esse equilíbrio de momentos fica assim:
Dividindo tudo por :
Passando para o outro lado, temos que:
E usando a relação de que , encontramos a outra componente de :
Como temos as duas componentes, já podemos dizer que encontramos a força .
Passo 3
Agora que temos a força de tração na haste, podemos avaliar os esforços internos na seção :
A vantagem de ter deixado a força já decomposta no passo anterior é que agora fica fácil encontrar as forças internas normal e cortante .
Aplicando o equilíbrio de forças na vertical e na horizontal:
Encontramos que:
Passo 4
Em seguida, precisamos encontrar a área da seção .
Usando a inclinação da haste para relacionar essa área com a área da seção transversal da haste:
Encontramos que:
Isolando a área , temos que:
Passo 5
Agora que encontramos as forças internas e e a área da seção , podemos calcular as tensões nessa seção.
Aplicando a fórmula da tensão normal média, temos:
Substituindo os valores encontrados para e :
Passando o para cima:
E agora para a tensão cisalhante média:
Substituindo os valores encontrados:
Passando o para cima:
Passo 6
Mas, na verdade, queremos descobrir os valores de correspondentes a certas tensões e .
Então vamos isolar nas expressões que encontramos no último passo.
Começando pela tensão normal média:
Isolando , temos:
Conhecemos a tensão normal máxima permitida na seção , , e a área da seção transversal da haste .
Mas ainda precisamos descobrir os valores de e de .
Para tanto, vamos olhar para a inclinação da haste:
Dessa imagem, conseguimos tirar que:
Além disso, sabemos que é igual ao cateto oposto de dividido pela hipotenusa, que pode ser encontrada pelo teorema de Pitágoras:
Substituindo todos esses valores na expressão anterior para :
Empurrando todas as unidade para o lado:
Como , então , o que significa que o resultado desses cálculos vai sair em .
Calculando tudo, isso dá:
Como esse número é um pouco grande, reescrevemos ele em :
Isso significa que a tensão normal máxima permitida na seção da haste implica que só podem ser aplicadas na viga cargas distribuídas de até .
Agora para a tensão cisalhante média:
Isolando , temos:
Substituindo a tensão cisalhante máxima permitida , a área e o valor encontrado para , temos:
Mais uma vez, o resultado de tudo isso vai sair em . Calculando tudo, isso dá:
Reescrevendo em :
Ou seja, a tensão cisalhante máxima permitida na seção da haste implica que só podem ser aplicadas na viga cargas distribuídas de até .
Sendo assim, a tensão cisalhante é o fator limitante e a maior intensidade da carga uniforme que pode ser aplicada à estrutura é:
Resposta
Exercício Resolvido #8
Elaboração própria
Abaixo é dado uma treliça plana. Determine as tensões normais e cisalhantes que ocorrem na Barra AD, no plano 39°. Todas as barras são quadradas com seção (40x40)cm.
Passo 1
Antes de qualquer conta precisamos o passo a passo de solução do nosso problema. Por se tratar de uma treliça plana sabemos que os únicos esforços que apareceram são os esforços normais. Como queremos calcular só uma barra, calculamos o valor do normal nela. Depois que fizermos isso teremos uma barra com um esforço normal, basta decompor ele no plano a 39° e fazer a conta para as tensões que já sabemos que tem as seguintes fórmulas
Vamos lá então.
Passo 2
Vamos primeiro descobri o normal na nossa barra resolvendo a nossa treliça.
Primeiro calculamos as reações dos apoios
Fazendo o somatório de momentos igual a zero no ponto A teremos que
Por consequência teremos que
Como já temos as reações de apoio, vamos fazer o equilíbrio de forças no nó A
Precisamos agora decompor o normal
Mas como determinamos esse ?
Com isso podemos determinar as relações trigonométricas do nosso triangulo
Passo 3
Vamos fazer a decomposição do nosso normal agora
se fizermos o equilíbrio da nossa peça teremos que
Resolvendo o primeiro sistema teremos que
Passo 4
Agora que já temos o nosso carregamento, vamos analisar a nossa barra
Agora já sabemos o plano que está agindo assim como o carregamento. Agora precisamos fazer uma decomposição de vetores. Um vetor será perpendicular ao plano, ou seja, normal ao plano, logo podemos calcular com ele a nossa tensão normal. O outro vetor será paralelo ao plano, ou podemos dizer que causará um esforço cortante, nesse caso essa força nos dará a tensão cisalhante. Dessa forma teremos que
Fazendo a decomposição de forças teremos que
Passo 5
Agora que já temos os esforços, falta determinarmos as tensões, sabemos que a fórmula para tensão é
Mas temos que tomar muito cuidado, porque essa área não é da seção transversal, mas da seção do plano orientado a 39°, como calcularemos essa área?
Basta apenas olharmos a seção da seguinte maneira
Podemos ver que a relação entre área transversal e área da seção pode se dar por uma relação trigonométrica.
No enunciado é dito que a seção da nossa peça é 40x40 cm, logo teremos que
Substituindo na nossa equação teremos que
Passo 6
Agora só precisamos determinar as nossas tensões, temos que
Substituindo
Resposta
Exercício Resolvido #9
Elaboração própria
Uma barra de madeira de seção (30x30)cm está sujeita aos esforços mostrados abaixo. Usando seus conhecimentos de tensões normais e cisalhantes médias, determine as tensões que aparecem no plano indicado na figura. Atente-se para calcular as tensões no ponto indicado pelo plano.
Passo 1
Para resolver essa questão temos que tomar alguns cuidados. O primeiro é colocar todas as cargas fora do centro, no centro da peça, isso vai facilitar as contas que estamos fazendo.
Em seguida devemos destacar o plano que estaremos calculando as tensões, isso é importante pois é exatamente esse o objetivo da questão, logo temos que ter certeza de onde estamos fazendo a conta.
Passo 2
Agora já sabemos qual o plano que devemos calcular, assim como a sua orientação, mas que forças agem nele?
É bem fácil pegar esse esquema, é só você olhar a imagem anterior e se perguntar o seguinte. Quais forças estão faltando? Ou seja, que forças eu estava aplicando na minha peça e que não estão mais aparecendo? Serão exatamente essas forças que estarão agindo no nosso plano, e elas estão representadas aqui em baixo
Mas e aquele 10KN que sempre esteve antes do plano que estamos calculando?
Ele não entrará na conta, pois pelo nosso macete, só estará agindo no plano as forças que eu tirei quando destaquei o nosso plano D-D, isso é uma pegadinha, se você estiver distraído pode acabar somando esse 10 KN sem querer, então toma cuidado com isso.
Como só temos esses dois carregamentos agindo vamos transforma-los em um único vetor.
Passo 3
Agora já sabemos o plano que está agindo assim como o carregamento. Agora precisamos fazer uma decomposição de vetores. Um vetor será perpendicular ao plano, ou seja, normal ao plano, logo podemos calcular com ele a nossa tensão normal. O outro vetor será paralelo ao plano, ou podemos dizer que causará um esforço cortante, nesse caso essa força nos dará a tensão cisalhante. Dessa forma teremos que
E qual será o ângulo entre esses vetores? Basta usarmos a orientação do nosso plano, a sequência de passos abaixo nos mostra como fazer isso
Agora precisamos calcular os esforços normais e cisalhantes pela trigonometria do nosso triangulo. Logo teremos que
Passo 4
Agora que já temos os esforços, falta determinarmos as tensões, sabemos que a fórmula para tensão é
Mas temos que tomar muito cuidado, porque essa área não é da seção transversal, mas da seção do plano orientado a 30°, como calcularemos essa área?
Basta apenas olharmos a seção da seguinte maneira
Podemos ver que a relação entre área transversal e área da seção pode se dar por uma relação trigonométrica.
No enunciado é dito que a seção da nossa peça é 30x30 cm, logo teremos que
Substituindo na nossa equação teremos que
Passo 5
Agora só precisamos determinar as nossas tensões, temos que
Substituindo
Resposta
Exercício Resolvido #10
Elaboração própria
A barra abaixo foi submetida ao carregamento mostrado. Sabendo que o plano indicado na figura apresenta resistência ao cisalhamento de 893 KPa e resistência ao normal de 810 KPa, e que a seção da peça é quadrada com lado 37cm. Determine se os esforços mostrados seriam suficientes para romper a peça.
Passo 1
Para resolver essa questão temos que tomar alguns cuidados. O primeiro é colocar todas as cargas fora do centro, no centro da peça, isso vai facilitar as contas que estamos fazendo.
Vamos primeiro resolver as cargas da ponta.
Agora precisamos levar as cargas inclinas para o centro também, mas antes de fazer isso vamos fazer a decomposição desses vetores em duas parcelas, uma horizontal e uma vertical.
Usando as relações trigonométricas teremos que
Como já sabemos, temos que levar essas cargas para o meio da peça, mas note o seguinte, as cargas horizontais se somam, mas as cargas verticais se anulam, logo teremos que
Em seguida devemos destacar o plano que estaremos calculando as tensões, isso é importante pois é exatamente ele que nos ajudará a resolver a questão, logo temos que ter certeza de onde estamos fazendo a conta.
Passo 2
Agora já sabemos qual o plano que devemos calcular, assim como a sua orientação, mas que forças agem nele?
É bem fácil pegar esse esquema, é só você olhar a imagem anterior e se perguntar o seguinte. Quais forças estão faltando? Ou seja, que forças eu estava aplicando na minha peça e que não estão mais aparecendo? Serão exatamente essas forças que estarão agindo no nosso plano, e elas estão representadas aqui em baixo
Mas e aquele 20KN que sempre esteve antes do plano que estamos calculando?
Ele não entrará na conta, pois pelo nosso macete, só estará agindo no plano as forças que eu tirei quando destaquei o nosso plano a 45°, isso é uma pegadinha, se você estiver distraído pode acabar somando esse 20 KN sem querer, então toma cuidado com isso.
Como só temos esses três carregamentos agindo vamos transforma-los em um único vetor.
Passo 3
Agora já sabemos o plano que está agindo assim como o carregamento. Agora precisamos fazer uma decomposição de vetores. Um vetor será perpendicular ao plano, ou seja, normal ao plano, logo podemos calcular com ele a nossa tensão normal. O outro vetor será paralelo ao plano, ou podemos dizer que causará um esforço cortante, nesse caso essa força nos dará a tensão cisalhante. Dessa forma teremos que
E qual será o ângulo entre esses vetores? Basta usarmos a orientação do nosso plano, a sequência de passos abaixo nos mostra como fazer isso
Agora precisamos calcular os esforços normais e cisalhantes pela trigonometria do nosso triangulo. Logo teremos que
Passo 4
Agora que já temos os esforços, falta determinarmos as tensões, sabemos que a fórmula para tensão é
Mas temos que tomar muito cuidado, porque essa área não é da seção transversal, mas da seção do plano orientado a 45°, como calcularemos essa área?
Basta apenas olharmos a seção da seguinte maneira
Podemos ver que a relação entre área transversal e área da seção pode se dar por uma relação trigonométrica.
No enunciado é dito que a seção da nossa peça é 37x37 cm, logo teremos que
Substituindo na nossa equação teremos que
Passo 5
Agora só precisamos determinar as nossas tensões, temos que
Substituindo
Como foi dito no enunciado que a resistência ao normal é de 810 KPa e a resistência ao cisalhamento é de 893 KPa, vemos que a peça resistiria a tensão cisalhante já que
Porém a peça romperia devido a tensão normal, já que
Logo a resposta é que a peça rompe devido ao esforço normal
Resposta
A tensão cisalhante não rompe a peça
Mas a tensão normal rompe a peça