Potência e Torque
Produzido por Pablo RicardoTeoria
Nesse tópico, vamos ver:
- Como calcular o torque em motores ou engrenagens;
- Como desenhar torques em um diagrama de corpo livre;
- & como identificar os torques internos em diferentes trechos de um eixo.
Assim, vamos estar preparados para resolver qualquer exercício de torção. 👊
Introdução
A Dexter Motors, nossa empresa de consultoria automotiva, foi contratada para avaliar o sistema da figura abaixo.
Mais especificamente, precisamos determinar as tensões de cisalhamento máximas nos trechos e do eixo desse sistema:
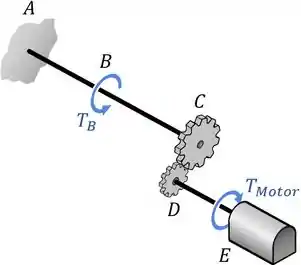
Olhando para essa figura, é difícil de saber até por onde começar.
Talvez se a gente já soubesse o valor dos torques internos e nos trechos e , poderíamos aplicar a fórmula da torção para esses trechos e pronto!
Mas na vida (e nos exercícios!) as coisas são um pouco mais difíceis. 😕
O mais provável é que o exercício nos forneça outras informações, como:
- A potência e a velocidade de rotação do motor;
- Os raios das engrenagens e ;
- E o valor do torque aplicado no ponto .
Então...
A partir desses dados, como é que a gente pode determinar os torques internos no nosso eixo ? 🤔
Vamos descobrir juntos!
Motores e Potência
A primeira coisa que podemos observar é que todo motor possui duas propriedades: uma potência e uma velocidade de rotação ou frequência .
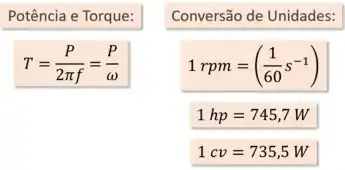
A partir dessas propriedades, podemos determinar o torque gerado por esse motor usando a fórmula:
Então assim, podemos dizer que o torque aplicado pelo nosso motor é .
Unidades
Para fazermos a conta , precisamos ter conhecimento das unidades de torque, potência e velocidade de rotação.
Quanto aos torques , normalmente eles são dados em unidades que já conhecemos, como “”, “” ou “”.
Já quanto à potência , ela deve ser preferencialmente dada em watts () ou em quilo-watts ().
Mas às vezes, ela pode ser dada em (horse-power) ou em (cavalo-vapor). Nesses casos, é preciso saber que:
Felizmente, a maioria dos professores fornece essas informações em prova caso elas sejam necessárias.
Por fim, quanto à velocidade de rotação , ela é normalmente dada em (rotações por minuto).
Para passar ela para o Sistema Internacional, precisamos dividir ela por para encontrarmos o seu valor em ou Hertz (), como no exemplo abaixo:
Velocidade Angular
Às vezes, um exercício pode te fornecer a velocidade angular (em radianos por segundo) de um motor ao invés de sua velocidade de rotação .
Nesse caso, basta saber que:
De tal forma que o torque vai ser:
Relações de Engrenamento
Então até aqui, já descobrimos como encontrar o torque aplicado no eixo e, consequentemente, na engrenagem do nosso sistema:
Agora, como é que a gente pode saber o torque que a engrenagem vai gerar na engrenagem ?
Para responder isso, temos que perceber que o torque em uma engrenagem é igual à força que é aplicada nos dentes dela vezes o raio dela:
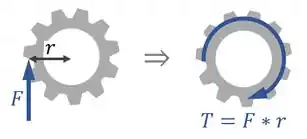
Assim, podemos dizer que:
E pelo princípio da ação e reação, temos que as forças que uma engrenagem faz na outra devem ser iguais.
Dessa forma, para um par de engrenagens e , temos que:
Assim, isolando o torque na segunda engrenagem, encontramos que:
Essa fórmula é uma relação de engrenagemento, e, através dela, podemos encontrar que, para as nossas engrenagens e , o torque em vai ser .
Sentido dos Torques em Engrenagens
Além disso, é importante saber que em um par de engrenagens, uma engrenagem gira em um sentido enquanto que a outra gira no outro:

No nosso caso, se a engrenagem tem um torque no sentido horário, a engrenagem vai ter um torque no sentido anti-horário.
Dessa forma, o eixo do nosso exemplo fica assim:
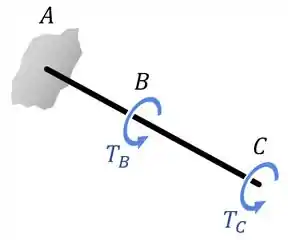
Regra da Mão Direita
Em seguida, um passo importante para estudar os torques em um eixo é fazer um diagrama de corpo livre desse eixo.
No nosso exemplo, os torques no ponto e na engrenagem estão no sentido anti-horário.
Então dá para imaginar que a parede em vai reagir com um torque no sentido horário para manter o eixo em equilíbrio:
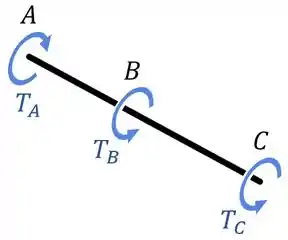
Agora, trabalhar com os torques assim em 3D não é muito prático.
Por esse motivo, a gente usa a regra da mão direita para fazer uma equivalência entre um torque em 3D e uma seta dupla:
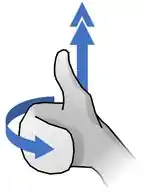
Usando essa regra, podemos fazer um diagrama de corpo livre do nosso eixo assim:

E usando esse diagrama de corpo livre, podemos, por exemplo, aplicar o equilíbrio de torques () nessa peça para encontrarmos que .
Torques Internos
Com tudo que já vimos, já conseguimos identificar os torques , e nos três pontos do nosso eixo.
Com isso, para podermos calcular as tensões de cisalhamento máximas no eixo, só nos falta identificar os torques internos nos trechos e do eixo.
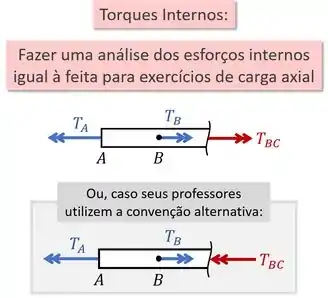
Para isso, fazemos uma análise dos esforços internos, igual à que fazíamos em problemas de carga axial:
- Secionamos a peça em seus diferentes trechos;
- Em cada seção, desenhamos um torque interno saindo da peça;
- E aplicamos o equilíbrio de torques para encontrar o valor desses torques internos.
Para o nosso exemplo, essas seções ficam assim:
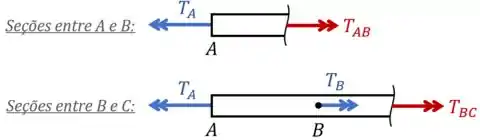
E através delas, conseguimos encontrar que e que .
Mas atenção! Para alguns professores, os torques internos são positivos quando estão “entrando” nas peças e devem então ser desenhados assim:
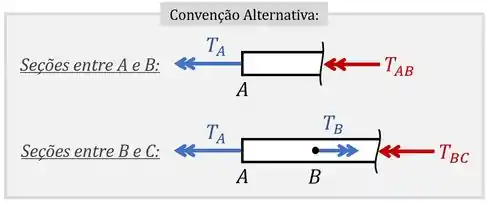
Usando essa convenção alternativa, encontraríamos que e que .
Como existe essa diferença nos resultados, vale a pena consultar qual é a convenção que os seus professores usam.
Resumo

Rola sim! 😉
Aqui vai:

Pronto.
Agora é a sua hora de mandar ver nos exercícios!
Motores e Potência
Relações de Engrenamento
Regra da Mão Direita
Torques Internos
Resumo
Exercícios Resolvidos
Exercício Resolvido #1
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 189-3.64.
Determine a tensão de cisalhamento máxima em um eixo de seção transversal cheia, de de diâmetro, quando ele transmite a uma velocidade de e .
Dica do Expert: .
Passo 1
O que está acontecendo?
O eixo tem um diâmetro e, consequentemente um raio .
Além disso, ele é maciço, e, dessa forma, possui um momento de inércia polar dado pela fórmula:
E, além disso, ele transmite uma potência com duas frequências: na letra e na letra .
Sendo que essa transmissão de potência se dá através de um torque que pode ser calculado pela fórmula:
Mas antes de podermos calcular o torque utilizando essa fórmula, precisamos converter a potência e a frequência para unidades do SI (sistema internacional).
E o que é que o exercício quer?
Ele quer saber a tensão de cisalhamento máxima no eixo em cada caso, que vai ser dada pela fórmula da torção:
Então resolver esse exercício é uma questão de:
- Converter a potência e a frequência para unidades do SI;
- Substituir as fórmulas do momento polar de inércia e do torque na fórmula da torção acima;
- E calcular o valor de para cada caso.
Passo 2
Então vamos começar pela conversão da potência e da frequência para unidades do SI.
Para a potência , temos que:
E que , o que significa que:
Já para a frequência , temos que:
E que ou , de tal forma que:
Passo 3
Transformadas as unidades de e , já podemos seguir para o cálculo de .
Para tanto, aplicamos a fórmula da torção:
No nosso caso, temos que e que , então:
Simplificando tudo, isso fica assim:
Passo 4
Encontrada uma expressão para , o último passo é calcular o seu valor nos itens e .
Para o item , temos que:
- ;
- ;
- & .
Substituindo esses valores na Equação 1, encontramos que:
O que dá:
O que é o mesmo que:
Já para o item , temos:
- ;
- ;
- & .
Substituindo esses valores na Equação 1, encontramos que:
O que dá:
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 134-5.5.
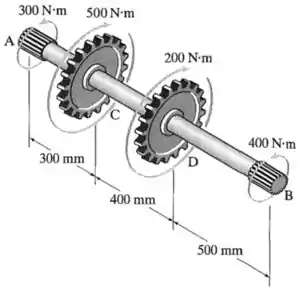
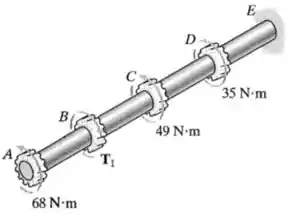
O eixo maciço de de diâmetro é usado para transmitir os torques aplicados às engrenagens. Determine a tensão de cisalhamento máxima absoluta no eixo.
Passo 1
O que está acontecendo?
O eixo maciço tem um diâmetro (e, consequentemente, um raio ) e está submetido à diferentes torques externos nos pontos , , e .
Sendo assim, ele vai resistir à diferentes torques internos nos trechos , e .
E o que é que o exercício quer?
Ele quer saber qual é a tensão de cisalhamento máxima absoluta no eixo.
Essa tensão máxima absoluta vai ocorrer no trecho do eixo que estiver resistindo ao maior torque interno .
Então o nosso primeiro passo vai ser identificar qual é o maior torque interno no eixo.
Feito isso, vamos poder usar a fórmula da torção para calcular a tensão de cisalhamento máxima absoluta no eixo:
Passo 2
Então vamos começar o exercício identificando qual é o maior torque interno no eixo.
E como é que a gente faz isso? 🤔
Do mesmo jeito que a gente encontrava a maior força interna normal em um eixo: fazendo um DCL (Diagrama de Corpo Livre) e uma análise dos esforços internos da peça.
Então vamos lá!
Primeiro, para fazer o DCL, usamos a regra da mão direita para representar os torques na forma de setas duplas:

Com isso, o nosso DCL fica assim:

Show! 😎
Agora, para encontrar os torques internos em cada trecho do eixo, fazemos uma análise dos esforços internos nas seções entre e , e & e :
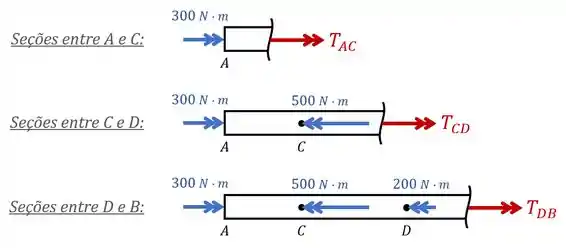
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.
Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.
Aplicando o equilíbrio de torques para cada caso, vamos ter que:
Em seguida, isolando os torques em cada uma dessas equações, encontramos que:
Com isso, percebemos que o torque de maior intensidade no nosso eixo é o torque que atua nas seções entre e ! 👌
Além disso, caso seja necessário, podemos representar o resultado que encontramos em um diagrama do momento torsor para o nosso eixo:
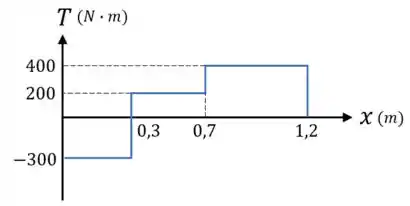
Dica do Expert:
Alguns professores permitem que você faça todo esse passo de cabeça e só diga “O maior torque acontece nas seções entre e , onde ”.
Por outro lados, existem outros professores, mais rígidos, que cobram que você faça tudo (DCL, análise dos esforços internos & diagrama do momento torsor) no papel. 😕
Passo 3
Agora que já identificamos o torque máximo na peça, podemos calcular a tensão de cisalhamento máxima absoluta.
Para tanto, vamos usar a fórmula da torção:
Por termos um eixo maciço, o momento polar de inércia vai ser dado por .
Além disso, como queremos saber a tensão máxima absoluta, devemos usar o torque máximo na peça, ou seja, .
Dessa forma, temos que:
Simplificando tudo, isso fica assim:
Por fim, substituindo os valores:
- ;
- & ,
Encontramos que:
E, usando que é o mesmo que , definimos a nossa resposta final:
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 138-5.33.
O projeto prevê que o eixo de transmissão de um automóvel será um tubo de parede fina. O motor transmite quando o eixo está girando a . Determine a espessura mínima da parede do eixo se o diâmetro externo for . A tensão de cisalhamento admissível do material é .
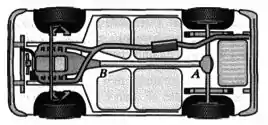
Passo 1
O que está acontecendo?
O eixo tem um diâmetro externo , e, consequentemente um raio externo .
Além disso ele não é maciço.
Ao invés disso, ele é feito de uma parede fina de espessura , de tal forma que ele possui um raio interno :
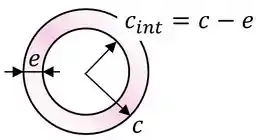
O eixo transmite uma potência a uma frequência , de tal forma que ele tem que suportar um torque :
E, por fim, o material do eixo possui uma tensão de cisalhamento admissível .
E o que é que o exercício quer?
Ele quer saber a espessura mínima da parede do eixo para que o torque transmitido não gere nele uma tensão de cisalhamento máxima maior que a admissível:
Sendo que essa tensão pode ser expressa pela fórmula da torção:
Onde é o momento polar de inércia do eixo e é dado pela fórmula abaixo para um eixo de seção vazada com raio externo e raio interno :
Passo 2
Antes de qualquer coisa, vamos converter as unidades da frequência para o sistema internacional.
Do enunciado, temos que:
Mas como , temos que:
O que significa que:
Passo 3
Agora sim, já temos tudo o que precisamos para pegar a condição de projeto e desenvolvê-la até encontrar a espessura mínima necessária para a parede do eixo.
Aplicando a condição de projeto, temos:
E em seguida, aplicando a fórmula da torção, temos que:
Substituindo a fórmula do momento polar de inércia para um eixo vazado e a fórmula do torque , isso fica assim:
Arrumando tudo, temos que:
Aqui, percebemos a necessidade de uma mudança de planos. 🤔
A ideia era substituir e isolar a espessura para encontrar seu valor mínimo.
Mas com a existência da potência no raio interno , fazer isso seria muito complicado.
Então vamos aceitar só encontrar o raio interno máximo possível por enquanto.
Daí, com o valor que encontrarmos, vamos usar que para calcular a espessura mínima necessária para o nosso eixo!
Passo 4
Partir isolar então para encontrar seu valor máximo possível!
Para tanto, começamos passando o termo para a direita:
E, em seguida, passamos para a esquerda:
Finalmente, isolamos :
Para encontrarmos que o valor máximo possível para é:
Substituindo nessa expressão:
- ;
- ;
- & ,
Encontramos que:
O que dá:
Passo 5
Agora que temos o máximo valor possível para , podemos encontrar o valor mínimo necessário para .
Aplicando que:
Isolando :
E substituindo:
- ;
- & ,
Encontramos que:
O que dá a nossa resposta:
Resposta
Exercício Resolvido #4
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 136-5.16.
O motor transmite um torque de ao eixo . Esse torque é transmitido ao eixo pelas engrenagens em e . Determine o torque de equilíbrio no eixo e a tensão de cisalhamento máxima em cada eixo. Os mancais , e permitem a livre rotação dos eixos.
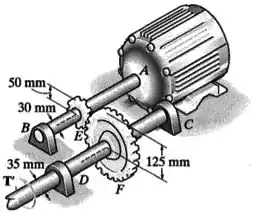
Passo 1
O que está acontecendo?
O motor transmite um torque ao eixo , que é maciço e possui um diâmetro , e, consequentemente, um raio .
Já o eixo também é maciço, mas possui um diâmetro , e, consequentemente, um raio .
E as engrenagens e possuem raios e .
Para saber torque que é gerado no eixo , é preciso perceber que o torque em uma engrenagem é igual à força que é aplicada nos dentes dela vezes o raio dela:
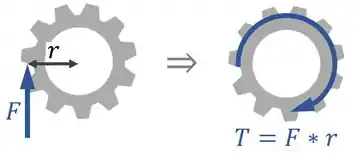
Assim, podemos dizer que:
E pelo princípio da ação e reação, é possível dizer que as forças que uma engrenagem faz na outra são iguais, de tal forma que, para as engrenagens e , temos que:
Mas a engrenagem faz parte do eixo , que gira com o torque , de tal forma que .
E a engrenagem faz parte do eixo , que gira com um torque desconhecido, de tal forma que .
Dessa forma, temos que:
O que significa que:
E o que é que o exercício quer?
Primeiro, ele quer que a gente encontre o torque de equilíbrio no eixo , que pode ser encontrado através da equação acima.
Depois, ele quer que saber a tensão de cisalhamento máxima em cada eixo, que pode ser encontrada aplicando a fórmula da torção abaixo para o eixo e para o eixo :
Passo 2
Então vamos começar encontrando o torque de equilíbrio no eixo pela relação de engrenamento:
Substituindo:
- ;
- ;
- & ,
Encontramos que:
O que dá:
Passo 3
Agora, vamos calcular as tensões de cisalhamento máxima em cada eixo.
Aplicando a fórmula da torção para o eixo , que está submetido a uma torção , temos:
Como o eixo é maciço, seu momento polar de inércia vai ser dado pela fórmula .
Dessa forma, temos que:
Simplificando, isso fica assim:
Finalmente, substituindo:
- ;
- & ,
- ;
- & ,
Encontramos que:
E, como é o mesmo que , isso significa que:
Já aplicando a fórmula da torção para o eixo , que está submetido a um torque , temos:
Mais uma vez, o eixo é maciço, então seu momento polar de inércia vai ser dado pela fórmula :
Simplificando, temos:
Por fim, substituindo:
Encontramos que:
Resposta
Exercício Resolvido #5
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 135-5.14.
O eixo maciço de alumínio tem diâmetro de e tensão de cisalhamento admissível . Determine o maior torque que pode ser aplicado ao eixo se ele também estiver sujeito a outros carregamentos de torção. Exige-se que aja na direção mostrada. Determine também a tensão de cisalhamento máxima no interior das regiões e .
Passo 1
O que está acontecendo?
O eixo maciço de diâmetro , e, consequentemente, raio tem uma tensão de cisalhamento admissível .
Fazendo um diagrama de corpo livre desse eixo (usando a regra da mão direita!), vemos os torques nos pontos , , e desse eixo, assim como a reação que surge no ponto :

Por causa desses diferentes torques, os diferentes trechos do eixo vão estar resistindo à diferentes torques internos.
E o que é que o exercício quer?
Ele quer saber o maior torque que pode ser aplicado no eixo.
O maior torque que pode ser aplicado é aquele que ainda garante que a tensão de cisalhamento máxima absoluta no eixo seja menor ou igual à admissível:
Então para resolver esse exercício, vamos:
1. Identificar a intensidade do maior torque interno sofrido pelo eixo, em função do torque aplicado.
& 2. Desenvolver a condição de projeto usando a fórmula da torção e isolar o torque desconhecido na expressão que for obtida.
Em seguida, o exercício ainda quer que a gente use o valor encontrado para para determinar a tensão de cisalhamento máxima no interior das regiões e .
Para isso, vamos usar, mais uma vez, a fórmula da torção.
Passo 2
Então vamos começar identificando a intensidade do maior torque sofrido pelo eixo.
Para tanto, precisamos fazer uma análise dos esforços internos no eixo.
Essa análise até pode ser feita de cabeça, mas alguns professores ainda requerem que ela seja feita no papel.
Então vamos lá!
Começamos a análise observando os esforços internos nas diferentes seções do eixo:
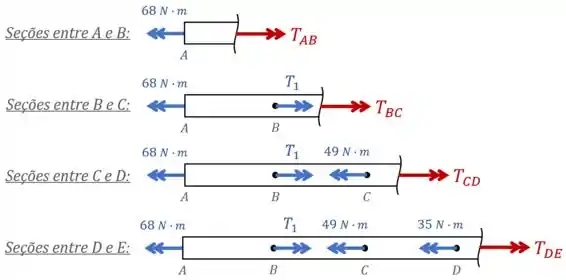
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.
Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.
Feito isso, aplicamos as condições de equilíbrio para cada uma das situações acima.
Nesse caso, a única condição de equilíbrio aplicável é o equilíbrio de torques:
Aplicando ele para cada caso, temos que:
Em seguida, isolando os torques em cada trecho, encontramos que:
Considerando que deve possuir um valor grande, podemos assumir que vai possuir uma intensidade maior que a intensidade de .
Assim, concluímos que a intensidade do maior torque sofrido pelo eixo é:
Passo 3
Em seguida, podemos desenvolver a nossa condição de projeto:
Aqui, temos que é a tensão de cisalhamento máxima absoluta.
Dessa forma, deve ser calculada usando a fórmula da torção e a intensidade do maior torque sofrido pelo eixo.
Sendo assim, temos que:
Substituindo isso na nossa condição de projetos, ela fica assim:
Em seguida, observamos que o momento polar de inércia do eixo maciço vai ser dado pela fórmula , de tal forma que:
Simplificando tudo, isso fica assim:
Isolando , temos que:
E substituindo:
- ;
- & ,
Encontramos que:
Como estamos trabalhando com , reescrevemos o resultado acima nessa unidade:
E finalmente, usando que , encontramos que:
Ou seja, o maior torque que pode ser aplicado é:
Passo 4
Resolvida a parte principal do exercício, agora vamos calcular os outros dois valores pedidos pelo exercício:
- A tensão de cisalhamento máxima para a região do eixo;
- E a tensão de cisalhamento máxima para a região .
Nesses dois casos, vamos usar a fórmula da torção:
Usar que o momento polar de inércia de um eixo maciço é :
E simplificar tudo para encontrar que:
Aplicando a fórmula acima para a região , temos que:
As barras de módulo são colocadas em volta do torque uma vez que esse torque vai ter um valor negativo, mas o cálculo de não se importa com os sinais do torque.
No Passo 2, vimos que .
Já no Passo 3, encontramos que .
Assim, temos que:
O que significa que:
Dessa forma, substituindo que:
- ;
- & ,
Na expressão que definimos para , encontramos que:
O que dá:
E como , isso significa que:
Fazendo o mesmo para a região , vamos ter que:
E que:
Assim, substituindo que:
- ;
- & ,
Na expressão que definimos para , encontramos que:
O que dá:
O que é o mesmo que:
E assim finalizamos o exercício!
Resposta
Exercício Resolvido #6
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 168-3.27.
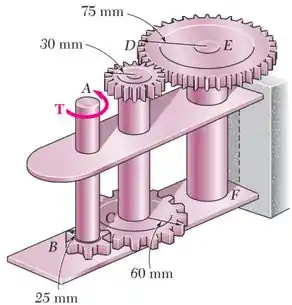
Um torque de intensidade é aplicado ao eixo do trem de engrenagem mostrado. Sabendo que a tensão de cisalhamento é de em cada um dos três eixos sólidos, determine o diâmetro necessário para o eixo , o eixo e o eixo .
Passo 1
O que está acontecendo?
Os eixos , e são maciços, possuindo:
- diâmetros , e ;
- E, consequentemente, raios .
Já as engrenagens , , , e possuem raios , , e , respectivamente.
E um torque é aplicado ao eixo .
Para descobrir o torque que é gerado nos demais eixos, é preciso perceber que o torque em uma engrenagem é igual à força que é aplicada nos dentes dela vezes o raio dela:
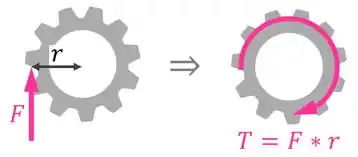
Assim, é possível dizer que:
E pelo princípio da ação e reação, é possível dizer que as forças que uma engrenagem faz na outra são iguais, de tal forma que, para as engrenagens e , por exemplo:
E o que é que o exercício quer?
Ele quer saber o diâmetro de cada um dos eixos para que a tensão máxima de cisalhamento neles seja igual à .
Para resolver o exercício, vamos primeiro encontrar o torque aplicado em cada engrenagem e em cada eixo.
Em seguida, vamos poder definir a tensão máxima de cisalhamento em cada eixo e descobrir o diâmetro necessário para cada eixo para que .
Passo 2
Então vamos começar encontrando o torque em cada engrenagem e em cada eixo do problema.
Primeiro, para o eixo , que gira junto com a engrenagem , sabemos que é aplicado nele um torque , de tal forma que:
Agora, devido às forças exercidas entre as engrenagens e , temos que:
O que significa que:
Substituindo , e , isso nos diz que:
Assim, para o eixo , temos que:
E devido às forças exercidas entre as engrenagens e , temos que:
O que significa que:
E substituindo , e , isso nos diz que:
E assim, para o eixo , temos que:
Passo 3
Agora, podemos definir a tensão máxima de cisalhamento para cada eixo.
Primeiro, sabemos que vai ser dada pela fórmula da torção:
E também sabemos que todos os eixos são maciços, de tal forma que .
Sendo assim, temos que:
Simplificando, isso fica assim:
E, como, em todos os casos, estamos querendo descobrir o diâmetro dos eixos, e não os raios , podemos fazer a substituição :
E arrumando tudo, isso fica assim:
Ainda podemos isolar o diâmetro dos eixos nessa equação para encontrar que:
Agora, só falta aplicar a equação acima para cada eixo e substituir sempre .
Passo 4
Começando pelo eixo , para resolver o item , temos que:
Substituindo:
- ;
- & ,
- ;
- & ,
- ;
- & ,
Encontramos que:
Seguindo com o eixo , para resolver o item , temos que:
Substituindo:
Encontramos que:
E finalizando com o eixo , para resolver o item , temos que:
Substituindo:
Encontramos que:
Resposta
Exercício Resolvido #7
Elaboração própria
Uma barra de aço AB e CD estão conectadas por duas engrenagens (E e F). A barra AB sofre a ação de um motor que transfere a ela uma potência de 50 HP a uma frequência de 180RPM. Sabendo que as dimensões de cada barra, assim como os diâmetros das engrenagens são dados na figura, determine a tensão cisalhante máxima ao qual a barra CD estará sujeita.
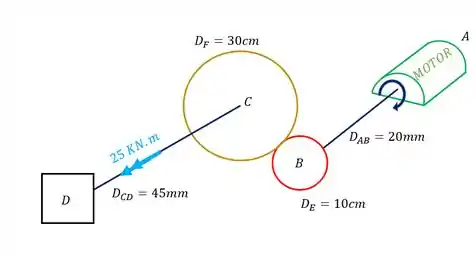
Passo 1
Nosso objetivo é determinarmos a tensão cisalhante na barra CD, mas antes dela temos muita coisa pra analisar. O nosso objetivo então é o seguinte, é trocar tudo que vem antes da barra CD por um toque equivalente a isso tudo, mas sempre respeitando as regras que temos que usar, basicamente o nosso objetivo é chegar nesse caso
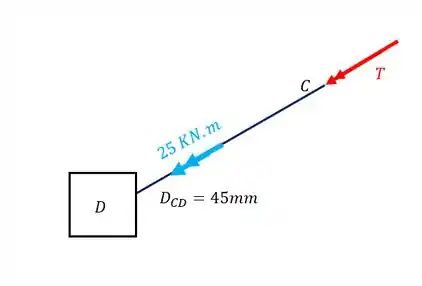
Quando chegarmos nessa situação usaremos a nossa fórmula para determinar o cisalhante máximo que é dado por
Mas para chegarmos nessa situação precisamos seguir um passo a passo.
Passo 2
Primeiro temos que nos livrar do nosso motor, ou seja, precisamos trocar o nosso motor por um torque equivalente no sentido mostrado na figura. Sabemos pela teoria que a fórmula que nos fornece isso é dada por
Em que é a potência do nosso motor e a frequência, ou seja, devemos nos precaver com o que se relaciona com as unidades. Então vamos lá.
Primeiro sabemos que a potência do nosso motor é dada por
Devemos ter na cabeça a conversão dessa unidade, alguns professores não gostam de dar esse valor na prova, então a nossa relação é
Convertendo teremos que
Também devemos ver a nossa frequência que é dada por
Se dividirmos esse valor por 60 acharemos a nossa frequência em Hz, além do mais, RPM são rotações por minutos, e Hz por segundo, logo fazendo a conversão teremos que
Agora que já temos os nossos valores basta substituir na nossa equação principal
Então a nossa figura agora será
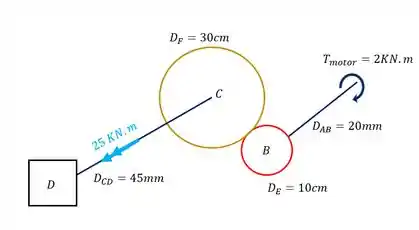
Passo 3
Para trocarmos a nossa barra AB é muito simples, se não há nela nenhum esforço torsor além do transferido pelo motor, significa que todo o esforço transferido pelo motor será transferido para a engrenagem E, como mostra a nossa figura.
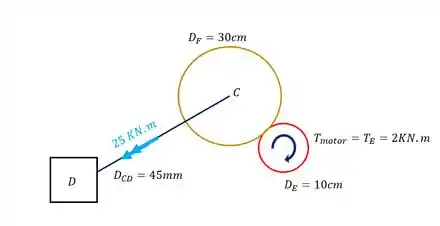
Passo 4
Agora temos que tomar cuidado pois se trata de uma relação entre engrenagens, se olharmos elas separadamente teremos o seguinte
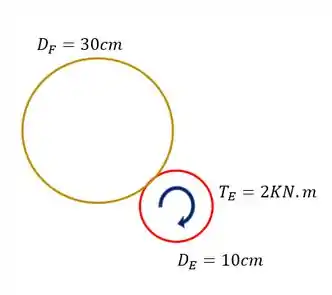
A primeira coisa que devemos saber é que, se a engrenagem E gira no sentido horário, então a engrenagem F girará no sentido anti-horário, da mesma forma ocorreria se os sentidos fossem invertidos, logo sabemos que os sentidos de giro serão
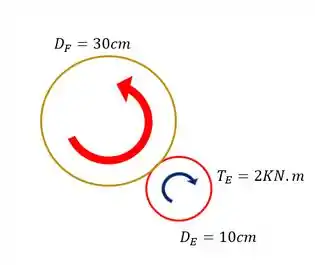
Agora que já sabemos os sentidos de giro precisamos analisar as nossas engrenagens separadamente
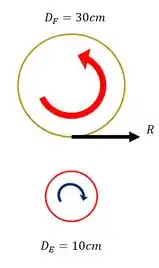
Sabemos que a engrenagem E empurra a engrenagem F com uma força R mostrada na figura, o que faz com que a engrenagem F gire.
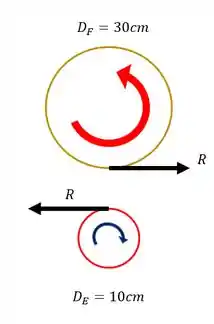
Sabemos também que pela terceira lei de newton aparecerá uma reação na engrenagem E, como o mostrado na figura acima.
Mas no que essas forças nos ajudam?
Sabemos que para calcularmos o torque nessas engrenagens, basta multiplicarmos a força pelo raio
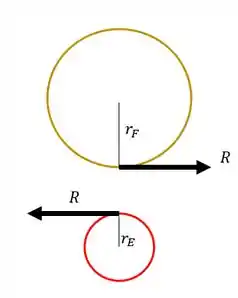
Para cada engrenagem teremos que
Como sabemos que o valor de R é igual pela lei da ação e reação teremos que
Igualando
Como nosso objetivo é determinar o valor de iremos isola-lo na fórmula
Substituindo teremos que
Substituindo na nossa fórmula teremos que
Olhando a nossa figura termos que o nosso torque está agindo da seguinte forma
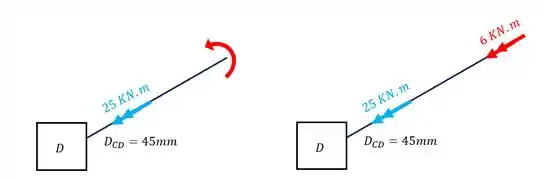
Onde enfim chegamos no objetivo inicial que tínhamos. Trocamos o Motor, a barra AB e as engrenagens E e F pelo nosso torque de 6KN.m.
Passo 5
Agora que já temos a nossa barra apenas precisamos analisar a nossa fórmula para tensão cisalhante máxima.
Primeiro sabemos que o cisalhante máximo é o ponto mais externo da nossa barra, ou seja
Também sabemos que o momento polar de inercia para seções circulares é dada por
Substituindo teremos que
Sabemos que
Falta ainda calcularmos o valor do torque.
Passo 6
Para calcularmos o torque precisamos dividir a nossa barra em dois pontos e ver em qual dos dois o torque será maior, como queremos o cisalhante máximo, usaremos o torque máximo.
Fazendo o diagrama de corpo livre teremos que
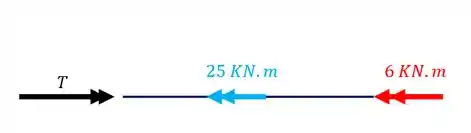
Fazendo o equilíbrio teremos que
Fazendo os dois cortes teremos que
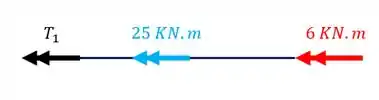
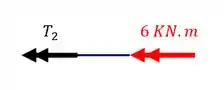
Então sabemos que devemos usar o maior valor para o cálculo
Passo 7
Substituindo os valores que encontramos teremos que
Resposta
Exercício Resolvido #8
Elaboração própria
Uma barra sofre uma torção mostrada na figura. Sabendo que essa torção foi dada na barra AB, determine qual deve ser o torque resistente na barra CD para que essa barra não sofra movimento. Os valores de diâmetro das engrenagens (E, F e G) e das barras é dado na própria figura.
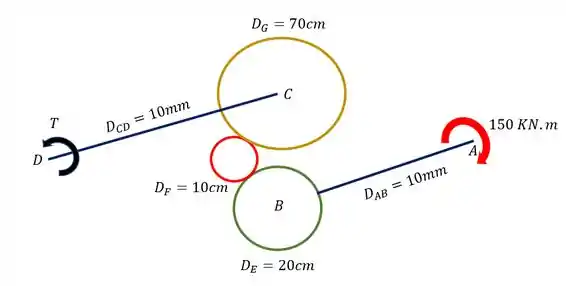
Passo 1
Para resolvermos esse exercício, precisamos fazer o torque que foi aplicado na barra AB, chegue na barra CD, só assim poderemos fazer o equilíbrio e saber qual será o torque que manterá o sistema parado. Vamos então ir trocando as nossas peças.
Começaremos tirando a nossa barra AB. Como ela não possui nenhum torque aplicado no comprimento dela, tendo apenas o inicial de intensidade , podemos transferir esse torque e esse sentido diretamente para a engrenagem E, olhando a nossa figura teremos que
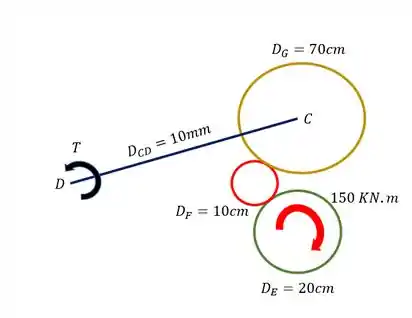
Passo 2
Agora temos que tomar cuidado pois se trata de uma relação entre engrenagens, se olharmos elas separadamente teremos o seguinte
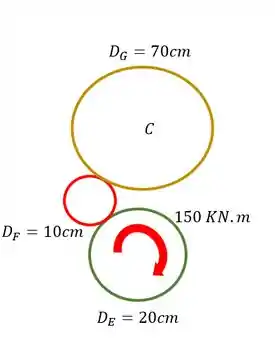
A primeira coisa que devemos saber é que, se a engrenagem E gira no sentido horário, então a engrenagem F girará no sentido anti-horário, da mesma forma se a engrenagem F gira no sentido anti-horário então a engrenagem G gira no sentido horário, sendo o mesmo princípio que ocorreria se os sentidos fossem invertidos, logo sabemos que os sentidos de giro serão
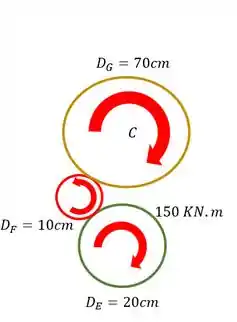
Agora que já sabemos os sentidos de giro precisamos analisar as nossas engrenagens separadamente
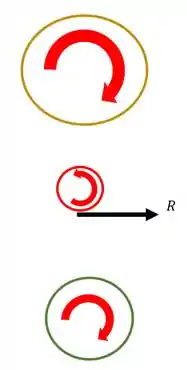
Sabemos que a engrenagem E empurra a engrenagem F com uma força R mostrada na figura, o que faz com que a engrenagem F gire.
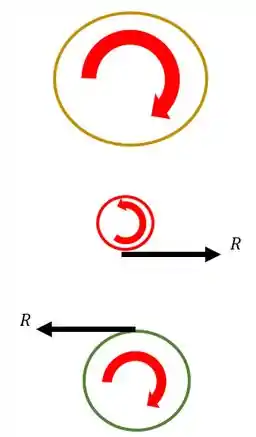
Sabemos também que pela terceira lei de newton aparecerá uma reação na engrenagem E, como o mostrado na figura acima.
Também sabemos que como a engrenagem F está acoplada na engrenagem G então está também aplicara uma força P na engrenagem G
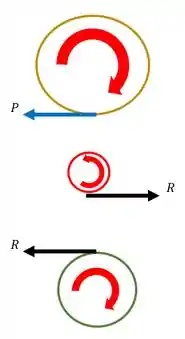
E da mesma forma, pela lei da ação e reação teremos uma reação na engrenagem F como mostra a figura
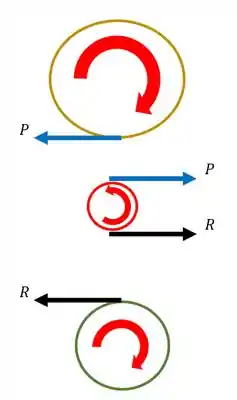
Mas no que essas forças nos ajudam?
Sabemos que para calcularmos o torque nessas engrenagens, basta multiplicarmos a força pelo raio
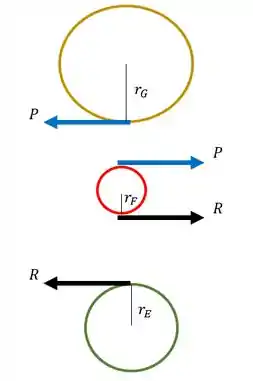
Para cada engrenagem teremos que
Como temos duas fórmulas para , podemos concluir que P=R
Como sabemos que o valor de R é igual pela lei da ação e reação teremos que
Igualando
Também teremos que
Como já sabemos que as forças são iguais, então podemos fazer a relação de engrenagens como
Como nosso objetivo é determinar , podemos fazer isso diretamente, ou por partes. Fazendo primeiro por partes teremos que
E em seguida faremos
Ou podemos fazer diretamente
sabemos que
Fazendo por partes teremos que
Em seguida faremos
Para conferir faremos também o cálculo direto
Oque comprova que a relação está correta.
Olhando a nossa figura termos que o nosso torque está agindo da seguinte forma
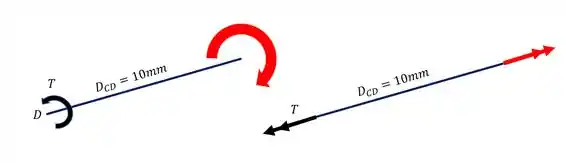
Onde enfim chegamos no objetivo inicial que tínhamos. Trocamos a nossa barra AB e as nossas engrenagens pelo nosso torque de 525KN.m.
Passo 3
Como nosso objetivo é determinar o valor do torque em D para que não ocorra movimento teremos que
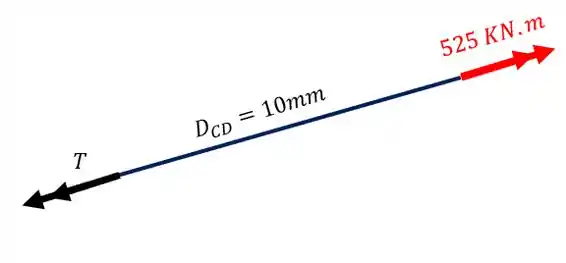
Fazendo o equilíbrio da nossa peça teremos que
Resposta
Exercício Resolvido #9
Elaboração própria
Uma barra de aço possui resistência ao cisalhamento de . Sabendo disso determine a potência máxima em HP que esse motor pode transferir para essa barra antes que a mesma rompa. Frequência do motor igual a Dimensões da barra dada na figura.
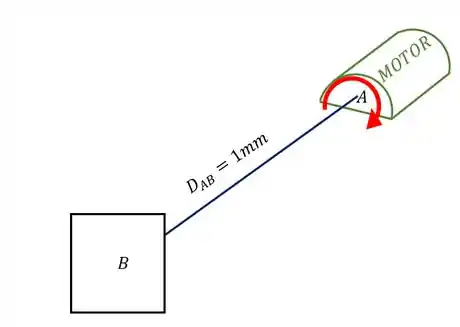
Passo 1
Queremos saber qual a máxima potencia do motor que aplicará um torque na barra sem que ela rompa, e já sabemos qual a relação entre torque e potência
Só que queremos o torque máximo que não rompe a barra, pois com o torque máximo teremos a potencia máxima, e para determinar o torque máximo devemos usar a fórmula.
Para termos o maior torque antes do rompimento devemos fazer
Primeiro sabemos que o cisalhante máximo é o ponto mais externo da nossa barra, ou seja
Também sabemos que o momento polar de inercia para seções circulares é dada por
Logo a nossa fórmula ficará
Substituindo teremos que
Passo 2
Agora temos duas equações
Isolando o valor do na segunda equação teremos que
Substituindo esse valor na primeira equação teremos que
Isolando o valor da potência teremos que
Cortando os valores teremos que
Passo 3
Analisando os valores teremos que
Substituindo na nossa equação teremos que
Lembrando da relação
Logo teremos que a potência é
Resposta
Exercício Resolvido #10
Elaboração própria
Um motor de potência 3000 HP e frequência 5400 RPM transfere para uma barra AB um torque. Sabendo que a resistência a tensão cisalhante da barra CD é , determine o diâmetro mínimo que a barra CD deverá ter, em mm, para que não rompa com a ação do torque aplicado pelo motor. Dimensões das engrenagens e da barra AB dados na figura.
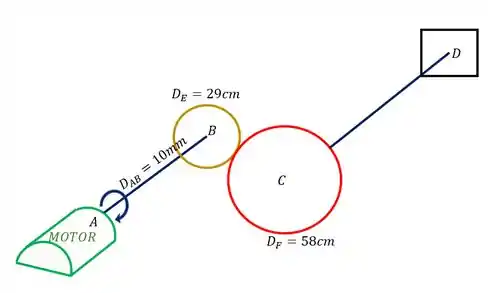
Passo 1
Nosso objetivo é determinarmos o raio mínimo da barra CD, mas antes dela temos muita coisa pra analisar. O nosso objetivo então é o seguinte, é trocar tudo que vem antes da barra CD por um toque equivalente a isso tudo, mas sempre respeitando as regras que temos que usar, basicamente o nosso objetivo é chegar nesse caso
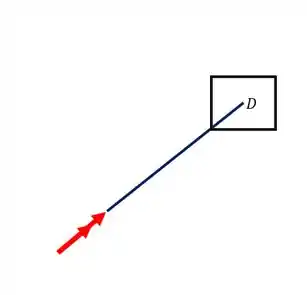
Quando chegarmos nessa situação usaremos a nossa fórmula para determinar o raio máximo que é dado por
Mas para chegarmos nessa situação precisamos seguir um passo a passo.
Passo 2
Primeiro temos que nos livrar do nosso motor, ou seja, precisamos trocar o nosso motor por um torque equivalente no sentido mostrado na figura. Sabemos pela teoria que a fórmula que nos fornece isso é dada por
Em que é a potência do nosso motor e a frequência, ou seja, devemos nos precaver com o que se relaciona com as unidades. Então vamos lá.
Primeiro sabemos que a potência do nosso motor é dada por
Devemos ter na cabeça a conversão dessa unidade, alguns professores não gostam de dar esse valor na prova, então a nossa relação é
Convertendo teremos que
Também devemos ver a nossa frequência que é dada por
Se dividirmos esse valor por 60 acharemos a nossa frequência em Hz, além do mais, RPM são rotações por minutos, e Hz por segundo, logo fazendo a conversão teremos que
Agora que já temos os nossos valores basta substituir na nossa equação principal
Então a nossa figura agora será
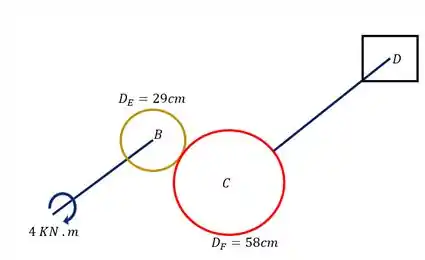
Passo 3
Para trocarmos a nossa barra AB é muito simples, se não há nela nenhum esforço torsor além do transferido pelo motor, significa que todo o esforço transferido pelo motor será transferido para a engrenagem E, como mostra a nossa figura.
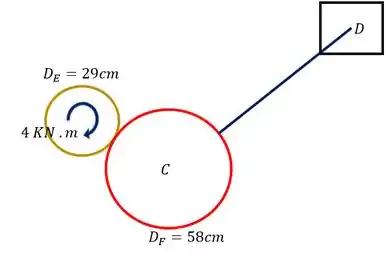
Passo 4
Agora temos que tomar cuidado pois se trata de uma relação entre engrenagens, se olharmos elas separadamente teremos o seguinte
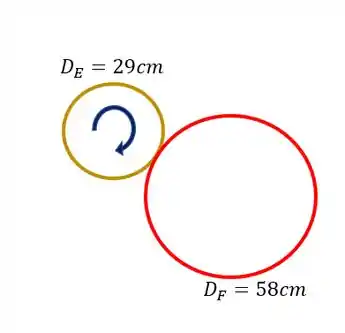
A primeira coisa que devemos saber é que, se a engrenagem E gira no sentido horário, então a engrenagem F girará no sentido anti-horário, da mesma forma ocorreria se os sentidos fossem invertidos, logo sabemos que os sentidos de giro serão
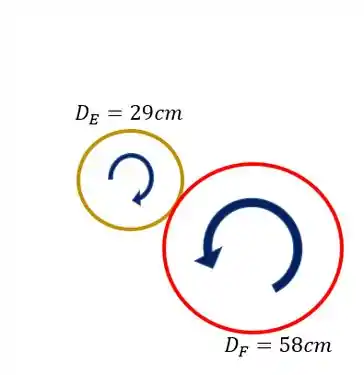
Agora que já sabemos os sentidos de giro precisamos analisar as nossas engrenagens separadamente
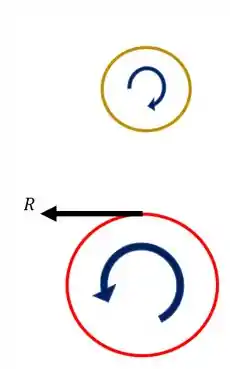
Sabemos que a engrenagem E empurra a engrenagem F com uma força R mostrada na figura, o que faz com que a engrenagem F gire.
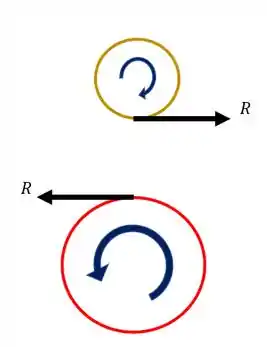
Sabemos também que pela terceira lei de newton aparecerá uma reação na engrenagem E, como o mostrado na figura acima.
Mas no que essas forças nos ajudam?
Sabemos que para calcularmos o torque nessas engrenagens, basta multiplicarmos a força pelo raio
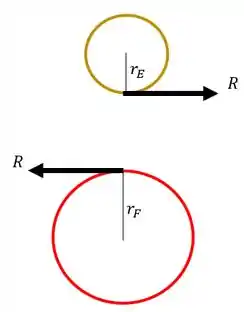
Para cada engrenagem teremos que
Como sabemos que o valor de R é igual pela lei da ação e reação teremos que
Igualando
Como nosso objetivo é determinar o valor de iremos isola-lo na fórmula
Substituindo teremos que
Substituindo na nossa fórmula teremos que
Olhando a nossa figura termos que o nosso torque está agindo da seguinte forma
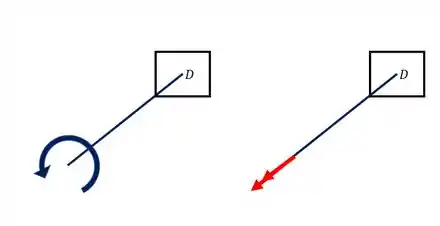
Onde enfim chegamos no objetivo inicial que tínhamos. Trocamos o Motor, a barra AB e as engrenagens E e F pelo nosso torque de 8 KN.m.
Passo 5
Agora que já temos a nossa barra apenas precisamos analisar a nossa fórmula para tensão cisalhante máxima.
Primeiro sabemos que o cisalhante máximo é o ponto mais externo da nossa barra, ou seja
Também sabemos que o momento polar de inercia para seções circulares é dada por
Uma ultima coisa que devemos saber é que como não queremos que a nossa barra não rompa devemos fazer
Substituindo teremos que
Isolando o valor de
Sabemos que
Substituindo teremos que
Mas precisamos do diâmetro, né: