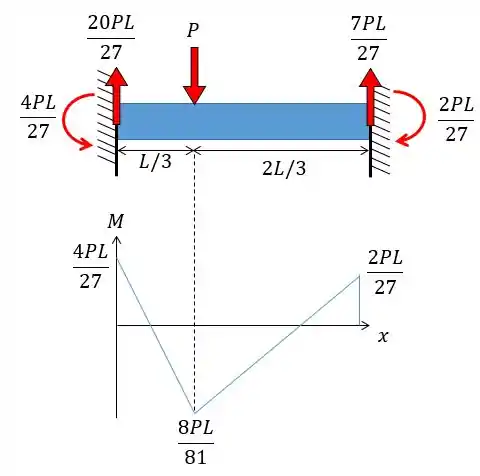
Determine as reações nos apoios e ; em seguida, trace o diagrama de momento fletor. Considere constante. Despreze o efeito da carga axial.
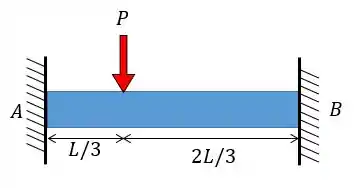
Passo 1
E aí, meus amores, tudo bom? Vamos resolver mais um exercício sobre vigas e nesse exercício a gente já consegue ver logo de cara que temos dois engastes logo se trata de uma viga hiperestático (ou estaticamente indeterminado). Caso você não tenha reparado olha só o diagrama de corpo livre dessa viga como fica:
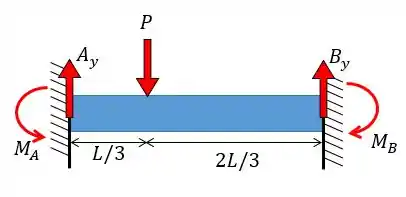
Reparem que o problema pediu para negligenciarmos as forças na horizontal, mas mesmo assim ainda temos 4 incógnitas para apenas três equações. Sendo assim, vamos precisar de mais uma equação para resolver essa questão.
Essa quarta equação será extamente a equação da força elástica. Que é dada por:
Então partiu resolver!!
Passo 2
A partir do nosso diagrama de corpo livre vamos achar as três primeira equações.
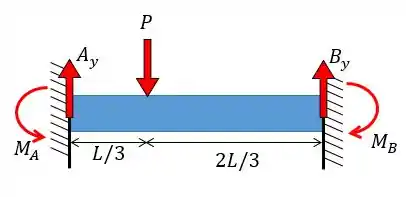
- Para a viga vertical:
- Para a viga horizontal não precisamos fazer já que negligenciaremos essa viga.
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Show! Temos duas na verdade já que deixamos a equação referente à horizontal de lado. Então vamso precisar de mais duas equações. Elas serão a da deflexão e da inclinação .
Passo 3
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Onde é a equação do momento fletor. Então a gente precisa saber como o momento fletor se comporta nessa viga. Aqui vamos utilizar uma função de descontinuidade, caso você não esteja lembrando direito não se preocupe vamos fazer isso bem devagar e seguindo a tabelinha abaixo:
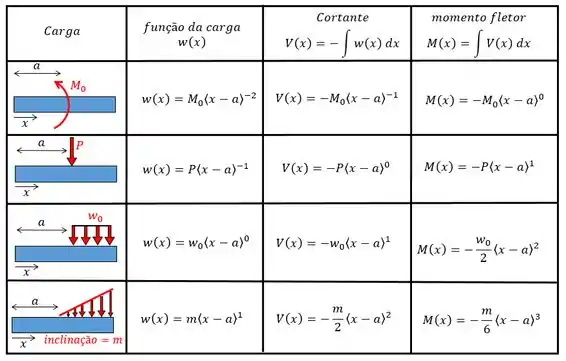
Essa viga possui dois momentos, como o momento fletor dado por uma carga-momento é dado, conforme a tabela, por:
Então para o nosso caso nós vamos ter:
Mas a viga não é composta só pelos momentos correto? Também temos as três forças. A tabela nos fornece que o momento fletor dado por uma força é do tipo:
Para as nossas três forças nós vamos ter:
Então o nosso momento fletor da viga como um todo é dado pelos momentos puros mais o momentos das forças:
Pessoal, aqui vale uma observação! Como na função de descontinuidade quando temos um termo negativo dentro do parêntesis bonitinho esse mesmo termo se torna nulo na realidade. Então nós podemos tirar os termos que aparecem porque esses termos sempre serão iguais a zero.
Sendo assim nossa equação fica da forma:
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
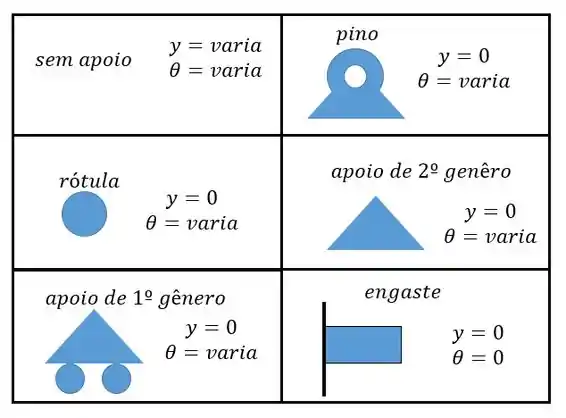
Então nós vamos ter as seguintes condições referentes aos dois engastes:
Na esquerda:
Na direita:
Belezinha! Agora é só substituir essas quatro condições de contorno na equação que temos da linha elástica!
Lembrando que os termos dentro do parêntesis bonitinho que sejam negativos serão desconsiderados, logo obtemos:
Substituindo:
obs: Perceba que vamos utilizar a equação da angulação () e não a da deflexão (). Lembre também que .
Substituindo e negligenciando os termos que seriam negativos dentro dos parêntesis:
Perceba que a gente já consegue achar a equação da linha elástica porque já encontramos nossas duas constantes. Mas a gente quer mais duas equações correto? Então vamos continuar com as condições de contorno.
Passo 6
Agora como então não tem termo negativo dentro dos parêntesis, assim não podemos negligencia-los.
Reorganizando:
Reorganizando:
Repare que agora encontramos mais duas equações exatamente como queríamos!
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
Passo 7
O problema também pediu para traçarmos o diagrama do momento fletor né? Colocando os resultados que achamos na nossa viga fica mais fácil de fazer:
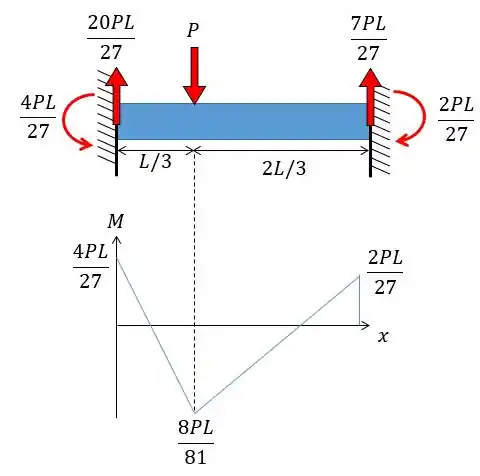
Resposta
Reações:
Diagrama: